Файл: Иркутский национальный исследовательский технический университет институт заочновечернего обучения Кафедра Самолётостроения и эксплуатации авиационной техники.docx

5.4 Третье приближение

1. 
   Требуется определить редукционные коэффициенты третьего приближения,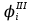 , для всех продольных ребер.
   

Для сжатого пояса они определяются следующим образом:



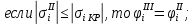
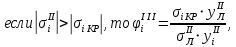
где 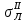, 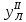- напряжения и ордината верхней, сжатой, полки главного лонжерона соответственно.

Для растянутого пояса:



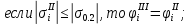
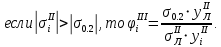
Верхние стрингеры необходимо редуцировать, так как напряжения в них превышают разрушающие:

Следовательно, для стрингеров с нумерацией 2…5 необходимо определить редукционные коэффициенты по формуле:

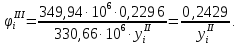
Для остальных продольных элементов редукционные коэффициенты остаются равными редукционным коэффициентам второго приближения, то есть 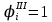. Полученные результаты приведены в таблице 5.3.

2. 
   В третьем приближении определяется смещение центральной оси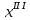 сечения относительно центральной оси второго приближения. Поскольку ординаты продольных элементов , приведенные в таблице 4.2, определены относительно хорды, то по соответствующей формуле смещение определится как:
   

3. 
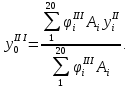
   Определение ординат продольных ребер относительно центральной оси, -го приближения:
   

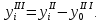
4. Вычисление осевого момента инерции сечения

---

, -го приближения: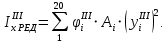

5. Вычисление напряжений в продольных ребрах, -го приближения: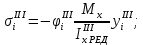



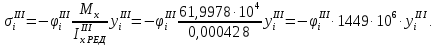
Все результаты вычислений для третьего приближения представлены в таблице 5.3.
Таблица 5.3 – Третье приближение

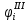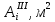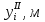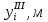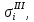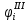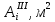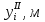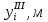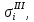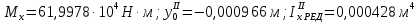1	1	0,001388	0,2296	0,2306	-333,84	20	1	0,001349	-0,2109	-0,2099	303,99
2	0,9575	0,000273	0,2537	0,2547	-353,05	19	1	0,000255	-0,2235	-0,2225	322,24
3	0,9281	0,000273	0,2617	0,2627	-352,97	18	1	0,000255	-0,2275	-0,2265	328,03
4	0,9281	0,000273	0,2617	0,2627	-352,97	17	1	0,000255	-0,2305	-0,2295	332,37
5	0,9537	0,000273	0,2547	0,2557	-353,04	16	1	0,000255	-0,2315	-0,2305	333,82
6	1	0,000273	0,2407	0,2417	-349,91	15	1	0,000255	-0,2315	-0,2305	333,82
7	1	0,000273	0,2217	0,2227	-322,40	14	1	0,000255	-0,2295	-0,2285	330,92
8	1	0,000273	0,1977	0,1987	-287,65	13	1	0,000255	-0,2265	-0,2255	326,58
9	1	0,000273	0,1717	0,1727	-250,00	12	1	0,000255	-0,2215	-0,2205	319,34
10	1	0,001178	0,1408	0,1418	-205,26	11	1	0,001133	-0,2086	-0,2076	300,66

---

6. Анализ результатов 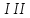-го приближения.

В верхней полке главного (первого) лонжерона напряжения меньше разрушающих:

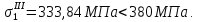
В нижней полке главного лонжерона напряжения так же меньше разрушающих:

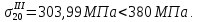
Напряжения в полках главного лонжерона не превышают разрушающие. Следовательно, можно выполнять четвертое приближение.

---

5.5 Четвертое приближение

4. 
   Требуется определить редукционные коэффициенты четвертого приближения,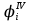 , для всех продольных ребер.
   

Для сжатого пояса они определяются следующим образом:



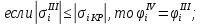
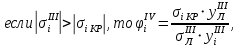
где 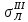, 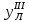- напряжения и ордината верхней, сжатой, полки главного лонжерона соответственно.

Для растянутого пояса:



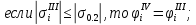
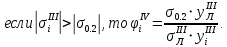
Верхние стрингеры необходимо редуцировать, так как напряжения в них превышают разрушающие:

Следовательно, для стрингеров с нумерацией 2…6 необходимо определить редукционные коэффициенты по формуле:

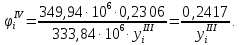
Для остальных продольных элементов редукционные коэффициенты остаются равными редукционным коэффициентам третьего приближения, то есть 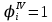. Полученные результаты приведены в таблице 5.4.

5. 
   В четвертом приближении определяется смещение центральной оси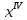 сечения относительно центральной оси третьего приближения. Поскольку ординаты продольных элементов , приведенные в таблице 4.2, определены относительно хорды, то по соответствующей формуле смещение определится как:
   

6. 
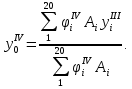
   Определение ординат продольных ребер относительно центральной оси,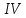 -го приближения:
   

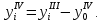
4. Вычисление осевого момента инерции сечения

---

, -го приближения: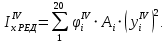

5. Вычисление напряжений в продольных ребрах, -го приближения: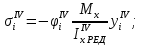



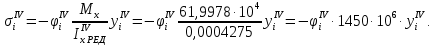
Все результаты вычислений для четвертого приближения представлены в таблице 5.4.
Таблица 5.4 – Четвертое приближение

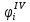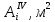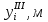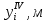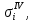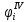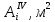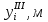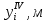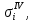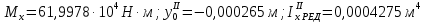1	1	0,001388	0,2306	0,2308	-334,72	20	1	0,001349	-0,2099	-0,2097	304,06
2	0,9487	0,000273	0,2547	0,2549	-350,68	19	1	0,000255	-0,2225	-0,2223	322,33
3	0,9197	0,000273	0,2627	0,2629	-350,63	18	1	0,000255	-0,2265	-0,2263	328,13
4	0,9197	0,000273	0,2627	0,2629	-350,63	17	1	0,000255	-0,2295	-0,2293	332,48
5	0,9449	0,000273	0,2557	0,2559	-350,68	16	1	0,000255	-0,2305	-0,2303	333,93
6	0,9999	0,000273	0,2417	0,2419	-350,77	15	1	0,000255	-0,2305	-0,2303	333,93
7	1	0,000273	0,2227	0,2229	-323,26	14	1	0,000255	-0,2285	-0,2283	331,03
8	1	0,000273	0,1987	0,1989	-288,46	13	1	0,000255	-0,2255	-0,2253	326,68
9	1	0,000273	0,1727	0,1729	-250,75	12	1	0,000255	-0,2205	-0,2203	319,43
10	1	0,001178	0,1418	0,1420	-205,95	11	1	0,001133	-0,2076	-0,2074	300,72

---