ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 293
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, ассоциаты из ее молекул заменяются отдельными молекулами, движущимися независимо друг от друга в газовой среде. Следовательно, стремление к увеличению неупорядоченности систем является движущим фактором самопроизвольных эндотермических процессов.
Так как изменение величин энтальпии ∆Н (и внутренней энергии ∆U) не дает однозначного ответа на вопрос о возможности самопроизвольного протекания химических реакций и физических процессов, то для этой цели введена еще одна термодинамическая функция, названная энтропией. Энтропия – это термодинамическая функция, характеризующая тепловое состояние систем, а также меру их неупорядоченности. Ее обозначают латинской прописной буквой S.
ЛЕКЦИЯ 5 1.3.2. Энтропия
Так как энтропия S – это функция состояния системы, то это означает, что также, как и внутренняя энергия, энтропия имеет конкретное численное значение, когда система находится в определенном состоянии. Дифференциал энтропии выражается следующим образом:
dS = dqобр/T, (1.76)
где dqобр – дифференциал теплоты в обратимом процессе, T – абсолютная температура. Употребление dqобр вместо dq указывает на то, что q не является функцией состояния, а зависит от пути, по которому осуществляется изменение. Однако для обратимого процесса dqобр/T представляет собой полный дифференциал. Изменение энтропии, сопровождающее данное изменение состояния не зависит от пути перехода. Изменение энтропии для конечного изменения от состояния 1 до состояния 2 получают интегрированием уравнения (1.76) по обратимому пути:
. (1.77)
Любой обратимый путь между состояниями 1 и 2 даст то же самое значение интеграла.
Подчеркнем, что понятие энтропии является не более сложным, чем понятие внутренней энергии. Действительно, каждая система обладает некоторым свойством, называемым внутренней энергией, причем ее возрастание dU при изменении можно найти, измеряя поглощенную при этом теплоту и вычитая совершенную системой работу. Каждая система также обладает некоторым свойством, называемым энтропией S, причем возрастание энтропии dS можно найти, измерив теплоту, поглощенную системой при обратимом процессе, и разделив ее на температуру T, при которой происходит поглощение теплоты. Следует отметить также, что при изложении термодинамики с применением методов статистической теории показано, что энтропия системы является мерой неупорядоченности ее состояния.
Макроскопические свойства веществ, с которыми имеет дело термодинамика, разделяются на две группы: интенсивные и экстенсивные. Интенсивные свойства не зависят от количества вещества (n) в системе. К ним относятся: температура T, давление p и плотность ρ. Экстенсивные свойства прямо пропорциональны количеству вещества или массе системы, если интенсивные свойства системы поддерживаются постоянными. Экстенсивными свойствами являются объем V и внутренняя энергия U. В данном разделе в термодинамику введено несколько новых экстенсивных свойств. Первое из этих свойств – энтропия S, далее – изохорный потенциал A (свободная энергия Гельмгольца) и изобарный потенциал G (свободная энергия Гиббса). Наряду с этим введено также несколько новых интенсивных свойств: химический потенциал μ и частные производные Vi, Ui, Hi, Si, Ai, Gi, соответствующих экстенсивных свойств по количеству вещества.
1.3.3. Выражение второго закона термодинамики через энтропию
Второй закон термодинамики рассматривают как постулат, о справедливости которого следует судить по результатам его применения. Они таковы – второй закон термодинамики справедлив для макроскопических систем, так как известно, что всегда выполняются все соотношения, выведенные из этого закона.
Имеются различные формулировки второго закона, которые звучат по-разному, но приводят к одним и тем же результатам. Английский физик У.Томсон (получивший за научные заслуги почетный титул лорда Кельвина) в 1851 году сформулировал второй закон следующим образом: невозможно использовать циклический процесс (ряд последовательных операций, которые возвращают систему в исходное состояние) для превращения в работу теплоты, взятой из теплового источника без одновременного переноса некоторого количества теплоты от более горячего тела к более холодному. Немецкий физик Р.Ю.Э. Клаузиус в 1850 году дал первую формулировку второго закона термодинамики в таком виде: невозможно использовать циклический процесс для переноса теплоты от более холодного тела к более горячему без одновременного превращения некоторого количества работы в теплоту. Из этих формулировок видно, что исторически развитие представлений о втором законе термодинамики было тесно связано с изучением тепловых машин. Так как такой подход далек от химии, то его надо было рассмотреть с использованием величин, которые можно непосредственно применить к химическим реакциям. Этот подход предложен в 1882 году немецким ученым Г.Л.Ф. Гельмгольцем и развит в дальнейшем американским физиком-теоретиком Д.У.Гиббсом. Он включал в себя понятие энтропии S.
Второй закон химической термодинамики можно сформулировать следующим образом: для любого бесконечно малого процесса дифференциал энтропии dS больше, чем dq/T или равен этой величине:
dS≥dq/T . (1.78)
Этим второй закон устанавливает различие между двумя типами изменений: изменения, для которых дифференциал энтропии больше dq/T (1.79), являются необратимыми (самопроизвольными), а изменения, для которых дифференциал энтропии равен dq/T (1.80), являются обратимыми:
dS>dq/T, (1.79)
dS = dq/T . (1.80)
К обратимым изменениям относится, например, перенос бесконечно малого количества теплоты от теплового резервуара с температурой T к резервуару, температура которого ниже на бесконечно малую величину (как, например, в процессе по рис. 1.12), или превращение бесконечно малого количества исходного вещества в продукт реакции в равновесной реакционной смеси.
На основании утверждения, что для необратимого процесса dS>dq/T, второй закон термодинамики дает критерий, позволяющий судить о возможности протекания химической реакции или физико-химического процесса. Только показав, что выполняется (1.79), можно утверждать, что этот процесс или реакция произойдут самопроизвольно.
Уравнение (1.78) удобно применять к изолированным системам с постоянной внутренней энергией U и постоянным объемом V, которые не обмениваются с окружающей средой ни теплотой, ни работой, ни веществом. Для таких систем dq=0, и уравнения (1.79), (1.80) приобретают следующий вид:
dS>0, (1.81)
в случае бесконечно малого необратимого изменения, и
dS = 0, (1.82)
в случае бесконечно малого обратимого изменения. Для конечного необратимого процесса в изолированной системе
∆S > 0, (1.83)
а для конечного обратимого процесса
∆S = 0. (1.84)
Таким образом, когда в изолированной системе происходит необратимое изменение, энтропия возрастает. Когда все возможности увеличения энтропии при самопроизвольных процессах будут исчерпаны, ее значение будет максимальным.
1.3.4. Расчет изменений энтропии для обратимых процессов
Три типа процессов, которые можно осуществить обратимо, включают: фазовые переходы (например, испарение жидкости с образованием насыщенного пара, кристаллизация или плавление при Tпл), нагревание вещества и расширение идеального газа. Для них легко рассчитать изменение энтропии. Например, в случае фазовых переходов, протекающих при постоянной температуре, интегрирование (1.77) дает:
S2 – S1 = ∆S = qобр/T,
где qобр – теплота, поглощенная при обратимом изменении.
Для одного моля вещества при постоянных температуре и давлении вместо (1.77) получим:
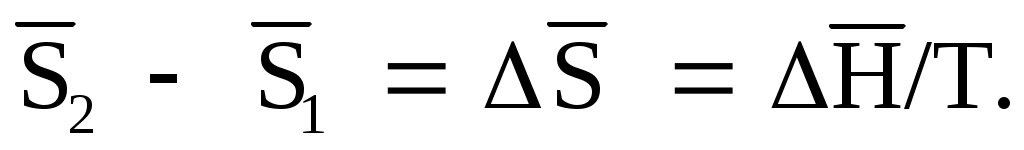(1.85)
Это уравнение можно использовать также для расчета энтропии возгонки или в случае изменения энтропии при переходе одной формы вещества в другую. Поскольку количество теплоты, полученной системой, равно количеству теплоты, отданному окружающей средой, то изменение энтропии окружающей среды равно изменению энтропии системы с обратным знаком. Суммарное изменение же энтропии для системы и окружающей среды равно нулю, если перенос теплоты происходит обратимо, как и требует уравнение (1.82).
Рассмотрим в качестве примера кипение н-гексана при 68,7 оС. При этой температуре теплота испарения н-гексана при атмосферном давлении равна 28,85∙103 Дж/моль. Если при этих условиях жидкость испаряется с образованием насыщенного пара, то процесс обратим, и изменение ее энтропии в расчете на один моль определяется уравнением (1.85):
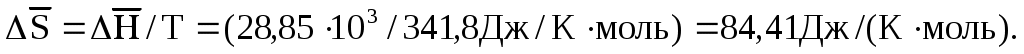
Мольная энтропия пара всегда больше, чем энтропия жидкости, с которой пар находится в равновесии, а мольная энтропия жидкости (учитывая (1.85)) всегда больше, чем энтропия твердого вещества в точке плавления. Действительно, согласно представлению об энтропии как о мере неупорядоченности системы, молекулы газа располагаются в пространства более беспорядочно, чем молекулы жидкости, а молекулы жидкости более неупорядочены, чем молекулы твердого тела:
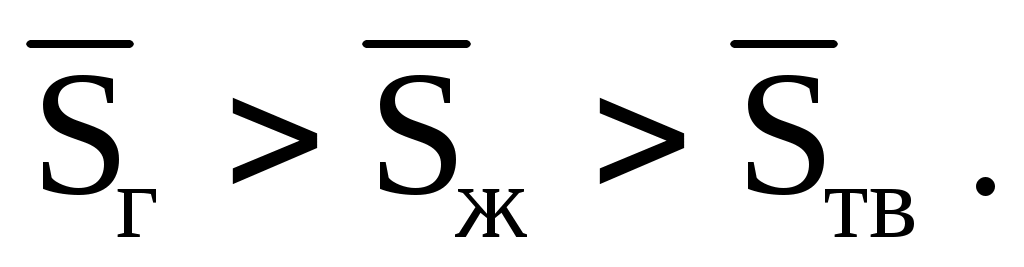(1.86)
Возрастание энтропии системы, вызванное увеличением температуры, можно рассчитать, так как изменение температуры можно осуществить обратимо. Если нагревание проводить при постоянном давлении, то теплота, поглощенная на каждой бесконечно малой стадии равна теплоемкости Ср, умноженной на бесконечно малый прирост температуры dT и, следовательно:
dS = Cр dT/T. (1.87)
Интегрирование уравнения (1.87) в пределах от T1 до Т2 дает:
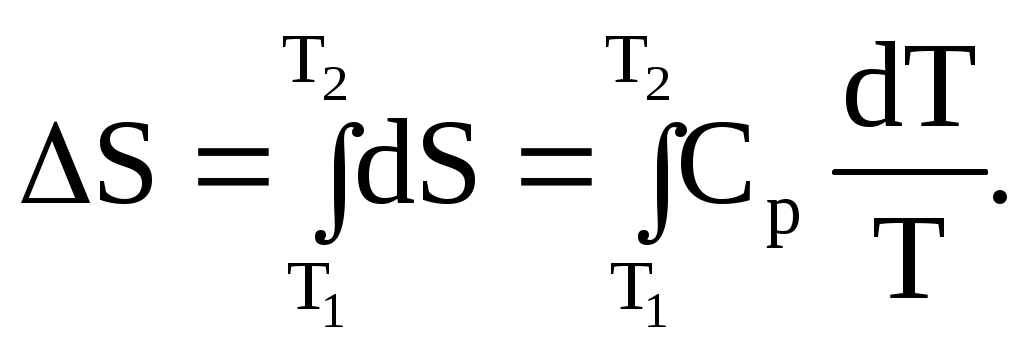(1.88)
Если Cp не зависит от температуры, то вместо (1.88) следует написать:
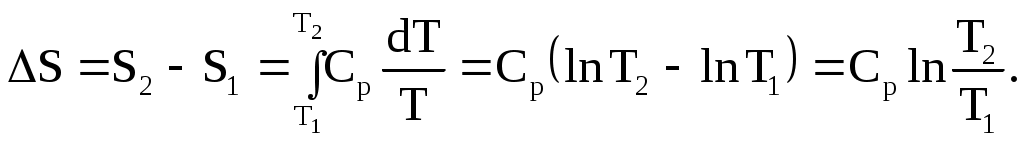(1.89)
Факт возрастания энтропии с ростом температуры согласуется с большей неупорядоченностью движения молекул при более высокой температуре. Если нагревание проводить при постоянном объеме, то вместо Ср используют Cv.
Рассмотрим далее, как изменяется энтропия идеального газа при обратимом увеличении температуры и объема. Для этого надо сообщать газу бесконечно малыми порциями теплоту dq. Тогда, в соответствии с первым законом термодинамики, для одного моля газа можно написать следующее уравнение:
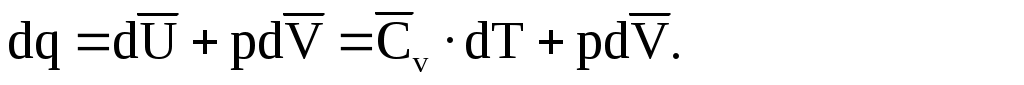(1.90)
Так как газ идеальный, то p = RT/V, и вместо (1.90) будет:
Так как изменение величин энтальпии ∆Н (и внутренней энергии ∆U) не дает однозначного ответа на вопрос о возможности самопроизвольного протекания химических реакций и физических процессов, то для этой цели введена еще одна термодинамическая функция, названная энтропией. Энтропия – это термодинамическая функция, характеризующая тепловое состояние систем, а также меру их неупорядоченности. Ее обозначают латинской прописной буквой S.
ЛЕКЦИЯ 5 1.3.2. Энтропия
Так как энтропия S – это функция состояния системы, то это означает, что также, как и внутренняя энергия, энтропия имеет конкретное численное значение, когда система находится в определенном состоянии. Дифференциал энтропии выражается следующим образом:
dS = dqобр/T, (1.76)
где dqобр – дифференциал теплоты в обратимом процессе, T – абсолютная температура. Употребление dqобр вместо dq указывает на то, что q не является функцией состояния, а зависит от пути, по которому осуществляется изменение. Однако для обратимого процесса dqобр/T представляет собой полный дифференциал. Изменение энтропии, сопровождающее данное изменение состояния не зависит от пути перехода. Изменение энтропии для конечного изменения от состояния 1 до состояния 2 получают интегрированием уравнения (1.76) по обратимому пути:
. (1.77)Любой обратимый путь между состояниями 1 и 2 даст то же самое значение интеграла.
Подчеркнем, что понятие энтропии является не более сложным, чем понятие внутренней энергии. Действительно, каждая система обладает некоторым свойством, называемым внутренней энергией, причем ее возрастание dU при изменении можно найти, измеряя поглощенную при этом теплоту и вычитая совершенную системой работу. Каждая система также обладает некоторым свойством, называемым энтропией S, причем возрастание энтропии dS можно найти, измерив теплоту, поглощенную системой при обратимом процессе, и разделив ее на температуру T, при которой происходит поглощение теплоты. Следует отметить также, что при изложении термодинамики с применением методов статистической теории показано, что энтропия системы является мерой неупорядоченности ее состояния.
Макроскопические свойства веществ, с которыми имеет дело термодинамика, разделяются на две группы: интенсивные и экстенсивные. Интенсивные свойства не зависят от количества вещества (n) в системе. К ним относятся: температура T, давление p и плотность ρ. Экстенсивные свойства прямо пропорциональны количеству вещества или массе системы, если интенсивные свойства системы поддерживаются постоянными. Экстенсивными свойствами являются объем V и внутренняя энергия U. В данном разделе в термодинамику введено несколько новых экстенсивных свойств. Первое из этих свойств – энтропия S, далее – изохорный потенциал A (свободная энергия Гельмгольца) и изобарный потенциал G (свободная энергия Гиббса). Наряду с этим введено также несколько новых интенсивных свойств: химический потенциал μ и частные производные Vi, Ui, Hi, Si, Ai, Gi, соответствующих экстенсивных свойств по количеству вещества.
1.3.3. Выражение второго закона термодинамики через энтропию
Второй закон термодинамики рассматривают как постулат, о справедливости которого следует судить по результатам его применения. Они таковы – второй закон термодинамики справедлив для макроскопических систем, так как известно, что всегда выполняются все соотношения, выведенные из этого закона.
Имеются различные формулировки второго закона, которые звучат по-разному, но приводят к одним и тем же результатам. Английский физик У.Томсон (получивший за научные заслуги почетный титул лорда Кельвина) в 1851 году сформулировал второй закон следующим образом: невозможно использовать циклический процесс (ряд последовательных операций, которые возвращают систему в исходное состояние) для превращения в работу теплоты, взятой из теплового источника без одновременного переноса некоторого количества теплоты от более горячего тела к более холодному. Немецкий физик Р.Ю.Э. Клаузиус в 1850 году дал первую формулировку второго закона термодинамики в таком виде: невозможно использовать циклический процесс для переноса теплоты от более холодного тела к более горячему без одновременного превращения некоторого количества работы в теплоту. Из этих формулировок видно, что исторически развитие представлений о втором законе термодинамики было тесно связано с изучением тепловых машин. Так как такой подход далек от химии, то его надо было рассмотреть с использованием величин, которые можно непосредственно применить к химическим реакциям. Этот подход предложен в 1882 году немецким ученым Г.Л.Ф. Гельмгольцем и развит в дальнейшем американским физиком-теоретиком Д.У.Гиббсом. Он включал в себя понятие энтропии S.
Второй закон химической термодинамики можно сформулировать следующим образом: для любого бесконечно малого процесса дифференциал энтропии dS больше, чем dq/T или равен этой величине:
dS≥dq/T . (1.78)
Этим второй закон устанавливает различие между двумя типами изменений: изменения, для которых дифференциал энтропии больше dq/T (1.79), являются необратимыми (самопроизвольными), а изменения, для которых дифференциал энтропии равен dq/T (1.80), являются обратимыми:
dS>dq/T, (1.79)
dS = dq/T . (1.80)
К обратимым изменениям относится, например, перенос бесконечно малого количества теплоты от теплового резервуара с температурой T к резервуару, температура которого ниже на бесконечно малую величину (как, например, в процессе по рис. 1.12), или превращение бесконечно малого количества исходного вещества в продукт реакции в равновесной реакционной смеси.
На основании утверждения, что для необратимого процесса dS>dq/T, второй закон термодинамики дает критерий, позволяющий судить о возможности протекания химической реакции или физико-химического процесса. Только показав, что выполняется (1.79), можно утверждать, что этот процесс или реакция произойдут самопроизвольно.
Уравнение (1.78) удобно применять к изолированным системам с постоянной внутренней энергией U и постоянным объемом V, которые не обмениваются с окружающей средой ни теплотой, ни работой, ни веществом. Для таких систем dq=0, и уравнения (1.79), (1.80) приобретают следующий вид:
dS>0, (1.81)
в случае бесконечно малого необратимого изменения, и
dS = 0, (1.82)
в случае бесконечно малого обратимого изменения. Для конечного необратимого процесса в изолированной системе
∆S > 0, (1.83)
а для конечного обратимого процесса
∆S = 0. (1.84)
Таким образом, когда в изолированной системе происходит необратимое изменение, энтропия возрастает. Когда все возможности увеличения энтропии при самопроизвольных процессах будут исчерпаны, ее значение будет максимальным.
1.3.4. Расчет изменений энтропии для обратимых процессов
Три типа процессов, которые можно осуществить обратимо, включают: фазовые переходы (например, испарение жидкости с образованием насыщенного пара, кристаллизация или плавление при Tпл), нагревание вещества и расширение идеального газа. Для них легко рассчитать изменение энтропии. Например, в случае фазовых переходов, протекающих при постоянной температуре, интегрирование (1.77) дает:
S2 – S1 = ∆S = qобр/T,
где qобр – теплота, поглощенная при обратимом изменении.
Для одного моля вещества при постоянных температуре и давлении вместо (1.77) получим:
(1.85)Это уравнение можно использовать также для расчета энтропии возгонки или в случае изменения энтропии при переходе одной формы вещества в другую. Поскольку количество теплоты, полученной системой, равно количеству теплоты, отданному окружающей средой, то изменение энтропии окружающей среды равно изменению энтропии системы с обратным знаком. Суммарное изменение же энтропии для системы и окружающей среды равно нулю, если перенос теплоты происходит обратимо, как и требует уравнение (1.82).
Рассмотрим в качестве примера кипение н-гексана при 68,7 оС. При этой температуре теплота испарения н-гексана при атмосферном давлении равна 28,85∙103 Дж/моль. Если при этих условиях жидкость испаряется с образованием насыщенного пара, то процесс обратим, и изменение ее энтропии в расчете на один моль определяется уравнением (1.85):
Мольная энтропия пара всегда больше, чем энтропия жидкости, с которой пар находится в равновесии, а мольная энтропия жидкости (учитывая (1.85)) всегда больше, чем энтропия твердого вещества в точке плавления. Действительно, согласно представлению об энтропии как о мере неупорядоченности системы, молекулы газа располагаются в пространства более беспорядочно, чем молекулы жидкости, а молекулы жидкости более неупорядочены, чем молекулы твердого тела:
(1.86)Возрастание энтропии системы, вызванное увеличением температуры, можно рассчитать, так как изменение температуры можно осуществить обратимо. Если нагревание проводить при постоянном давлении, то теплота, поглощенная на каждой бесконечно малой стадии равна теплоемкости Ср, умноженной на бесконечно малый прирост температуры dT и, следовательно:
dS = Cр dT/T. (1.87)
Интегрирование уравнения (1.87) в пределах от T1 до Т2 дает:
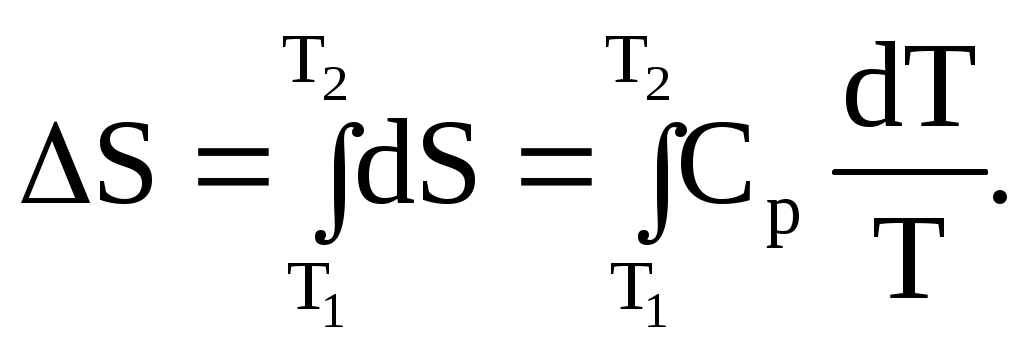(1.88)Если Cp не зависит от температуры, то вместо (1.88) следует написать:
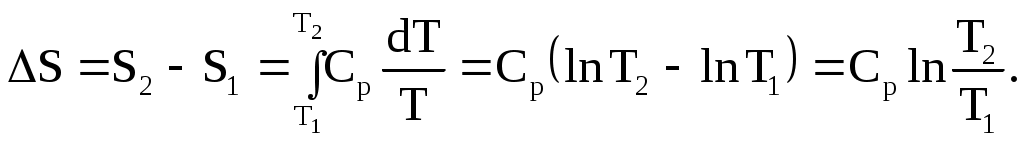(1.89)Факт возрастания энтропии с ростом температуры согласуется с большей неупорядоченностью движения молекул при более высокой температуре. Если нагревание проводить при постоянном объеме, то вместо Ср используют Cv.
Рассмотрим далее, как изменяется энтропия идеального газа при обратимом увеличении температуры и объема. Для этого надо сообщать газу бесконечно малыми порциями теплоту dq. Тогда, в соответствии с первым законом термодинамики, для одного моля газа можно написать следующее уравнение:
(1.90)Так как газ идеальный, то p = RT/V, и вместо (1.90) будет: