Файл: Курсовая работа по динамике исследование колебаний механической системы с одной степенью свободы.doc
Добавлен: 12.12.2023
Просмотров: 199
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2.Определение закона движения системы.
3.Определение реакций внешних и внутренних связей.
4.С оставление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа.
5.Составление дифференциального уравнения движения механизма с помощью уравнения Лагранжа 2-го рода.
6.ПОСТРОЕНИЕ АЛГОРИТМА ВЫЧИСЛЕНИЙ
.
Подставляя (Определение закона движения системы..0) в (Определение закона движения системы..0), после несложных преобразований получим
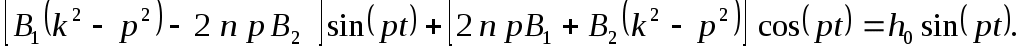
Сравнивая коэффициенты при соответствующих тригонометрических функциях справа и слева, получаем систему алгебраических уравнений для определения постоянных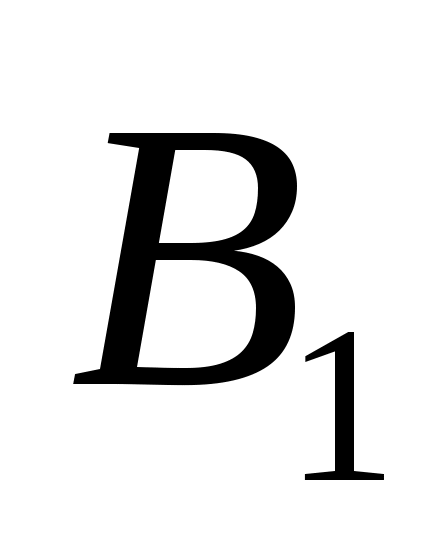 и
и 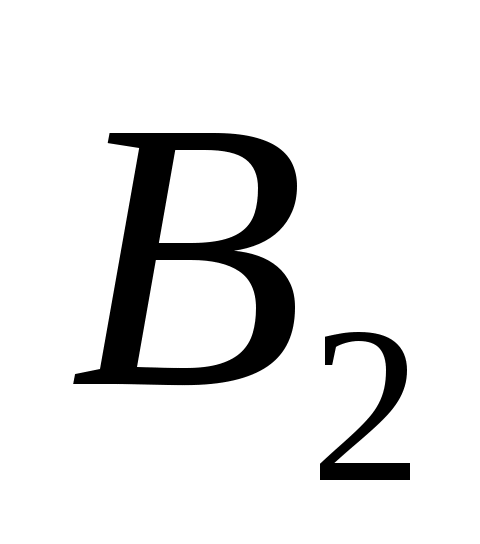 :
:
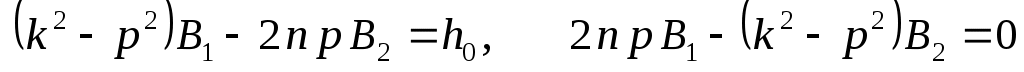 .
.
Решая эту систему алгебраических уравнений, получаем выражения для коэффициентов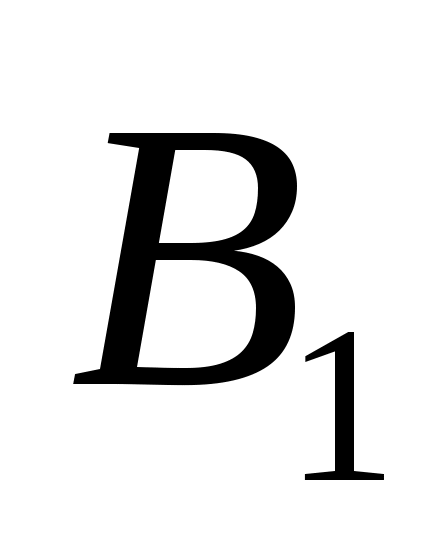 ,
, 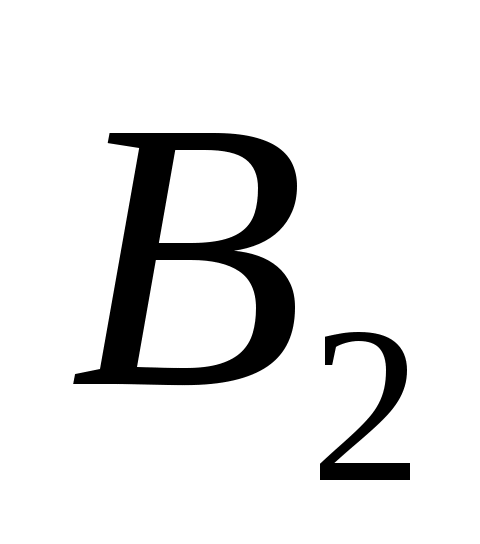 и
и 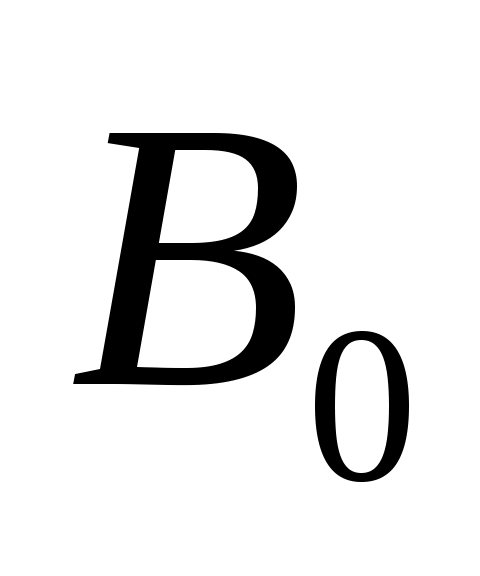 ,
, 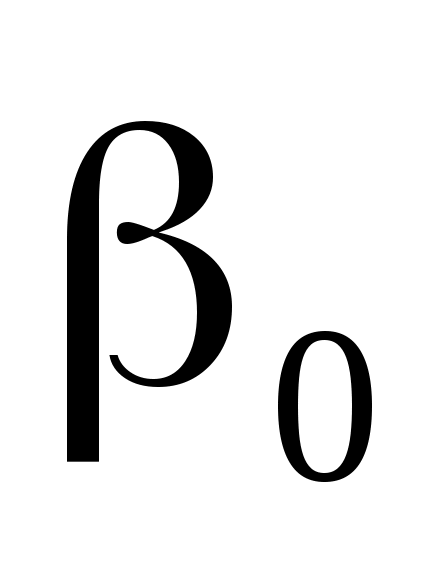 :
:
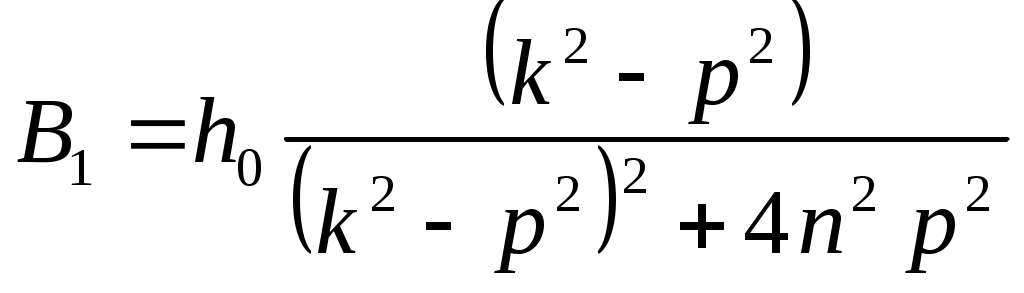 ;
; 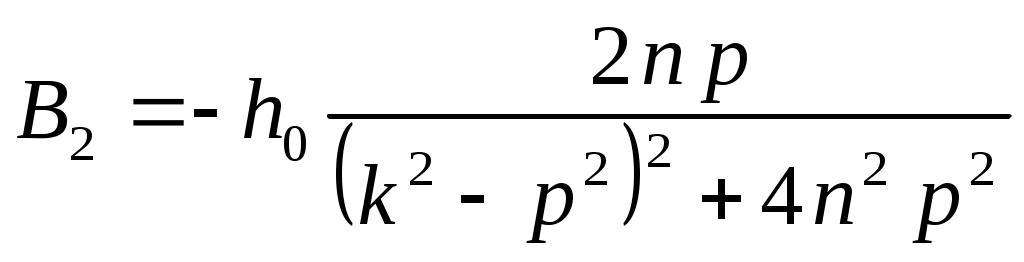 ;
;
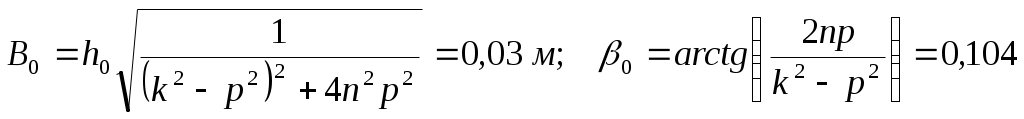 .
.
Таким образом, решение (Определение закона движения системы..0) найдено. Складывая (Определение закона движения системы..0) и (Определение закона движения системы..0), получаем общее решение неоднородного уравнения (Определение закона движения системы..0)
Подчинив (2.11) и (2.12) начальным условиям, получим систему уравнений относительно искомых констант
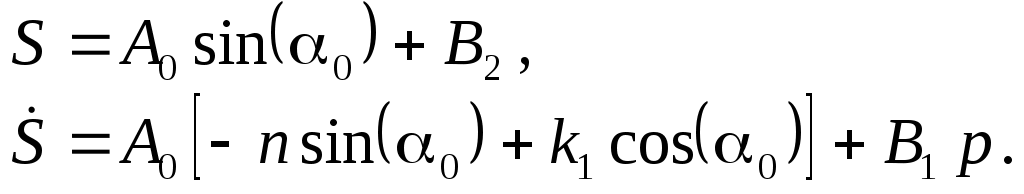
Решая эту систему, получаем:
И, подставляя (Определение закона движения системы..0) в (Определение закона движения системы..0), получаем закон движения механизма, выраженный через перемещение груза
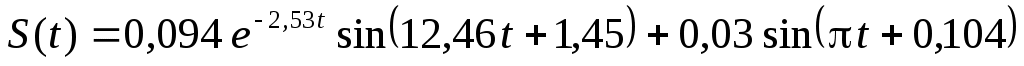 .
.
Для решения этой задачи расчленяем механизм на отдельные части и рисуем расчетные схемы отдельно для каждого тела (рис.3).
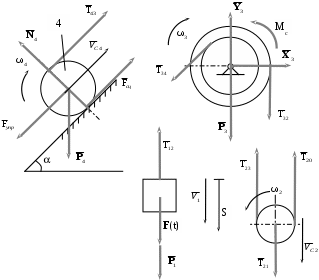
К каждому телу, изображенному на расчетной схеме (рис. 3.), применяем две из основных теорем механики материальной системы: теорему об изменении количества движения и теорему об изменении кинетического момента
Для каждого тела уравнения (3.1) и (З.2) записываем в проекциях на оси координат соответственно схемам рис. 3.:
С учетом кинематических соотношений (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) систему уравнений (Определение реакций внешних и внутренних связей..0) – (Определение реакций внешних и внутренних связей..0) преобразуем к виду:
Уравнения (Определение реакций внешних и внутренних связей..0) составляют систему алгебраических уравнений относительно функций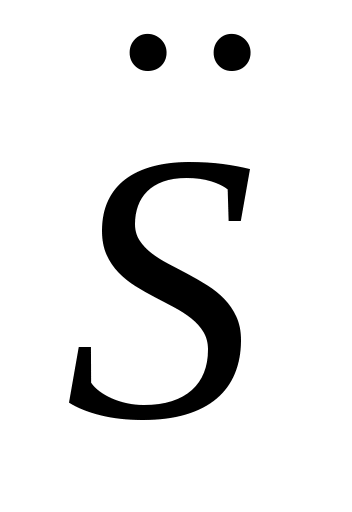 ,
, 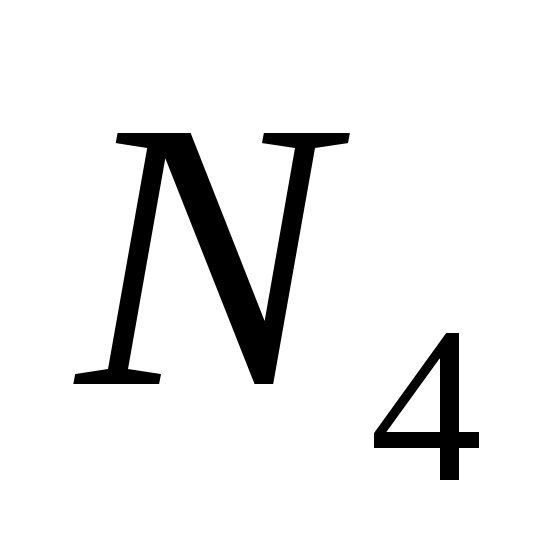 ,
, 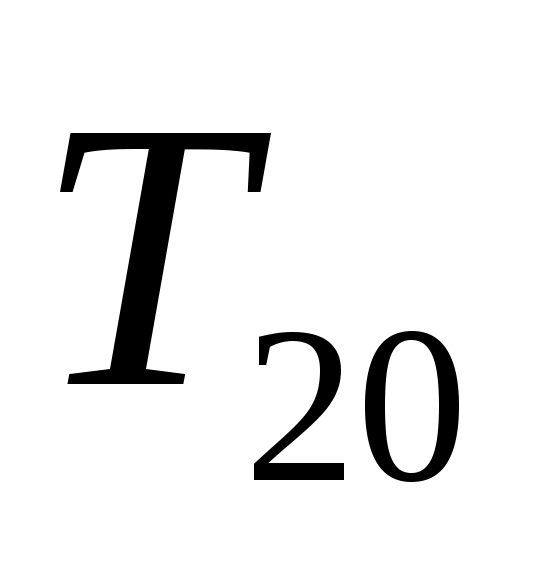 ,
, 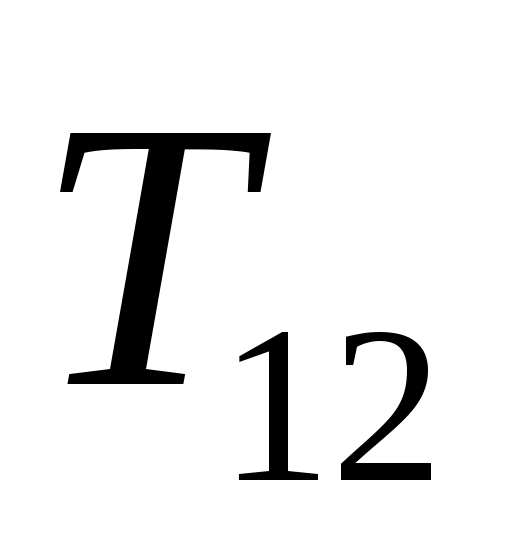 ,
, 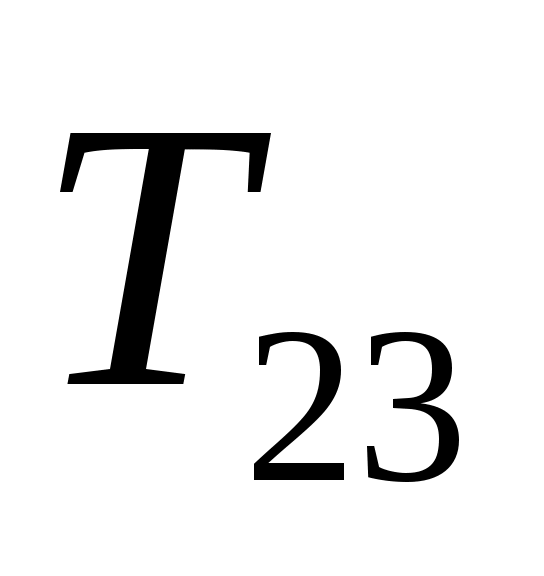 ,
, 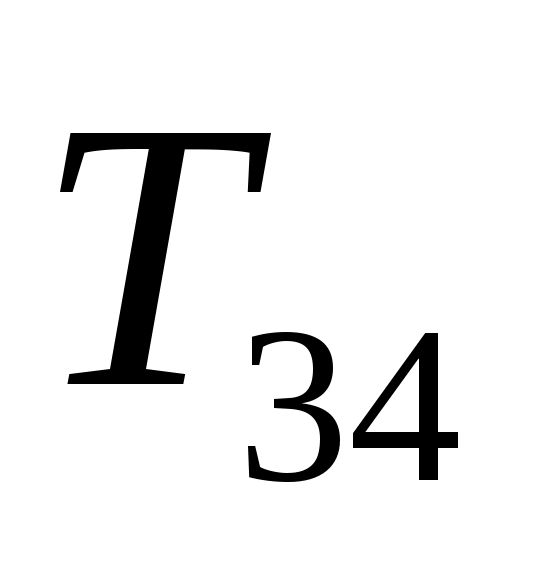 ,
, 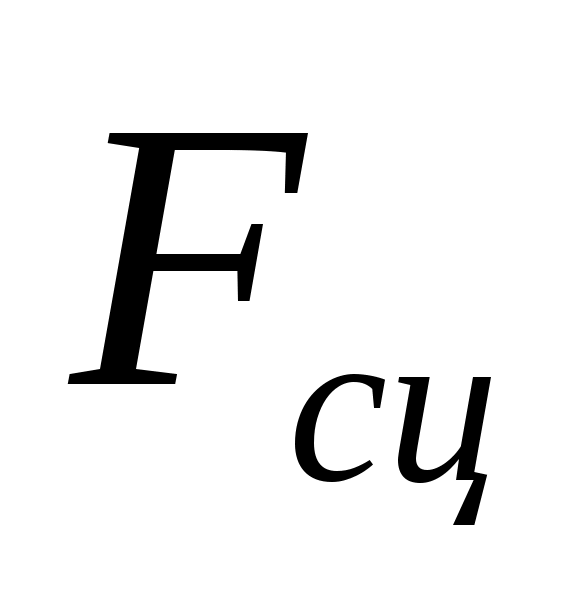 ,
, 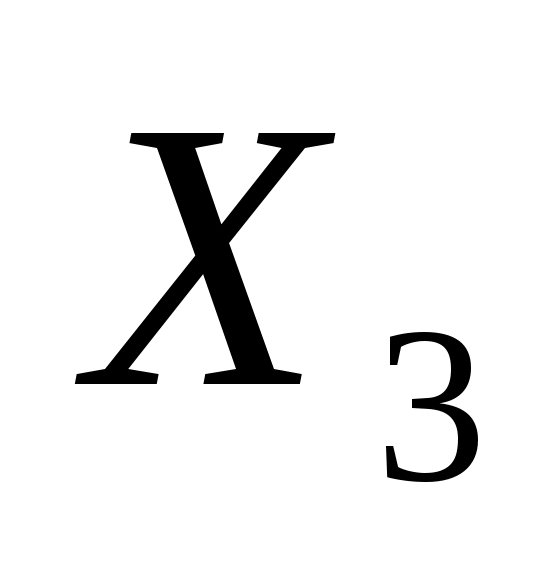 ,
, 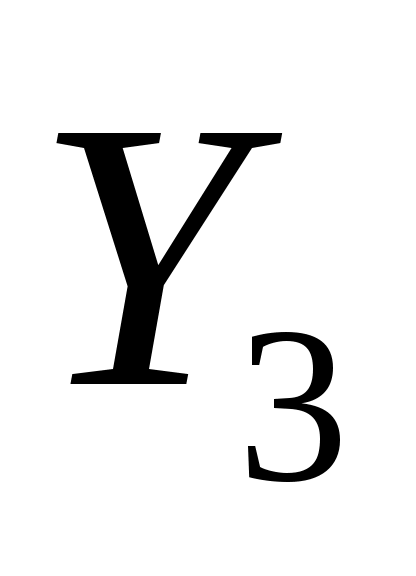 .
.
4.С
Общее уравнение динамики системы есть математическое выражение принципа Даламбера-Лагранжа
Здесь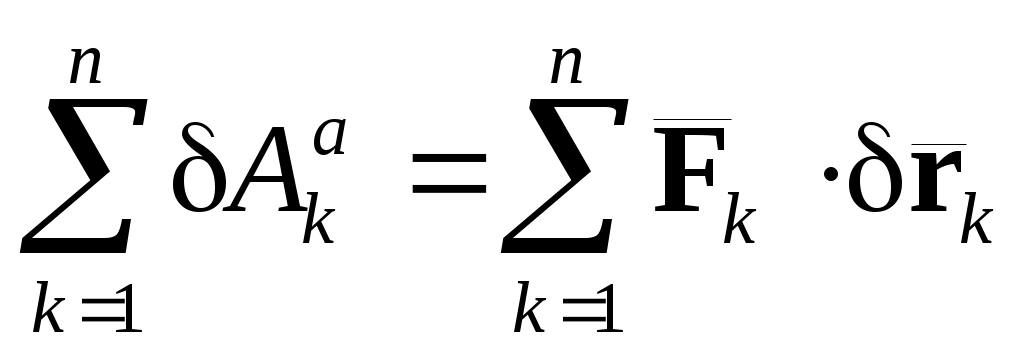 – сумма элементарных работ всех активных сил на возможном перемещении системы;
– сумма элементарных работ всех активных сил на возможном перемещении системы; 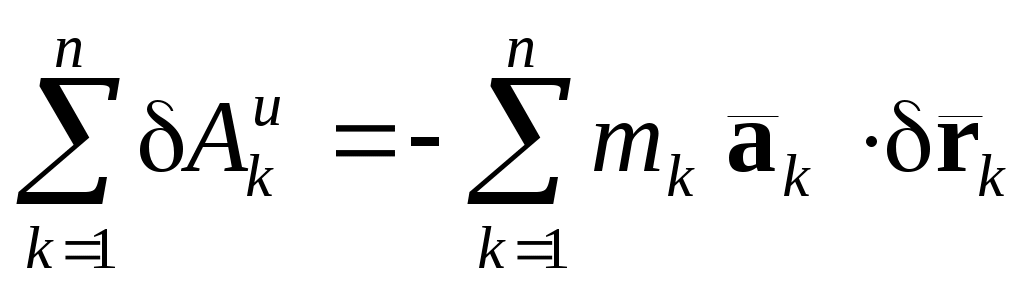 – сумма элементарных работ всех сил инерции на возможном перемещении системы.
– сумма элементарных работ всех сил инерции на возможном перемещении системы.
Изобразим на рисунке активные силы и силы инерции (рис. 4).
Сообщим системе возможное перемещение. Возможная работа активных сил определяется как сумма следующих элементарных работ:
Сумма элементарных работ указанных сил вычисляется, как и мощность по формуле (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0)
Подставляя (Определение закона движения системы..0) в (Определение закона движения системы..0), после несложных преобразований получим
Сравнивая коэффициенты при соответствующих тригонометрических функциях справа и слева, получаем систему алгебраических уравнений для определения постоянных
Решая эту систему алгебраических уравнений, получаем выражения для коэффициентов
Таким образом, решение (Определение закона движения системы..0) найдено. Складывая (Определение закона движения системы..0) и (Определение закона движения системы..0), получаем общее решение неоднородного уравнения (Определение закона движения системы..0)
| | | (Определение закона движения системы..0) | |
| Константы | (Определение закона движения системы..0) | ||
Подчинив (2.11) и (2.12) начальным условиям, получим систему уравнений относительно искомых констант
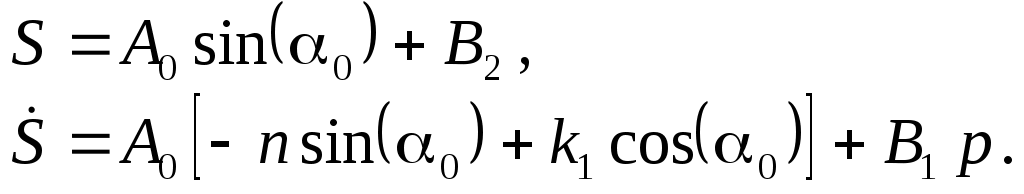
Решая эту систему, получаем:
| | 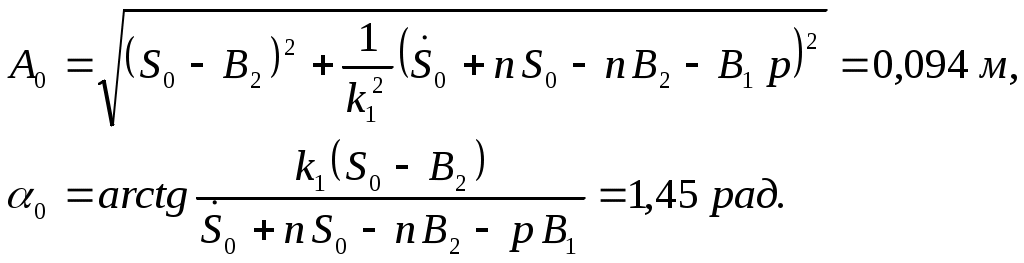 | (Определение закона движения системы..0) |
И, подставляя (Определение закона движения системы..0) в (Определение закона движения системы..0), получаем закон движения механизма, выраженный через перемещение груза
3.Определение реакций внешних и внутренних связей.
Для решения этой задачи расчленяем механизм на отдельные части и рисуем расчетные схемы отдельно для каждого тела (рис.3).

-
Расчетные схемы для каждого тела механизма.
К каждому телу, изображенному на расчетной схеме (рис. 3.), применяем две из основных теорем механики материальной системы: теорему об изменении количества движения и теорему об изменении кинетического момента
| | | (Определение реакций внешних и внутренних связей..0) |
| | | (Определение реакций внешних и внутренних связей..0) |
Для каждого тела уравнения (3.1) и (З.2) записываем в проекциях на оси координат соответственно схемам рис. 3.:
| тело 1: | | (Определение реакций внешних и внутренних связей..0) |
| тело 2: | | (Определение реакций внешних и внутренних связей..0) |
| тело3: | 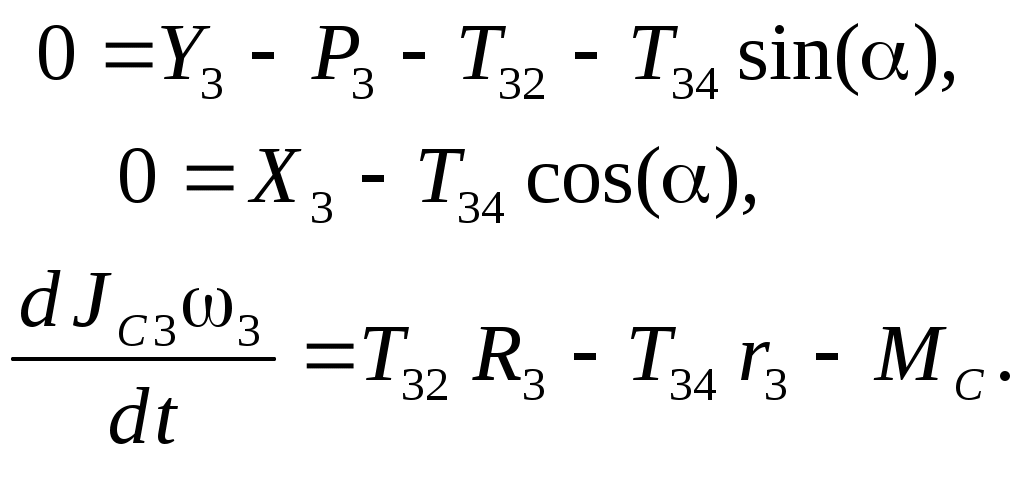 | (Определение реакций внешних и внутренних связей..0) |
| тело4: | 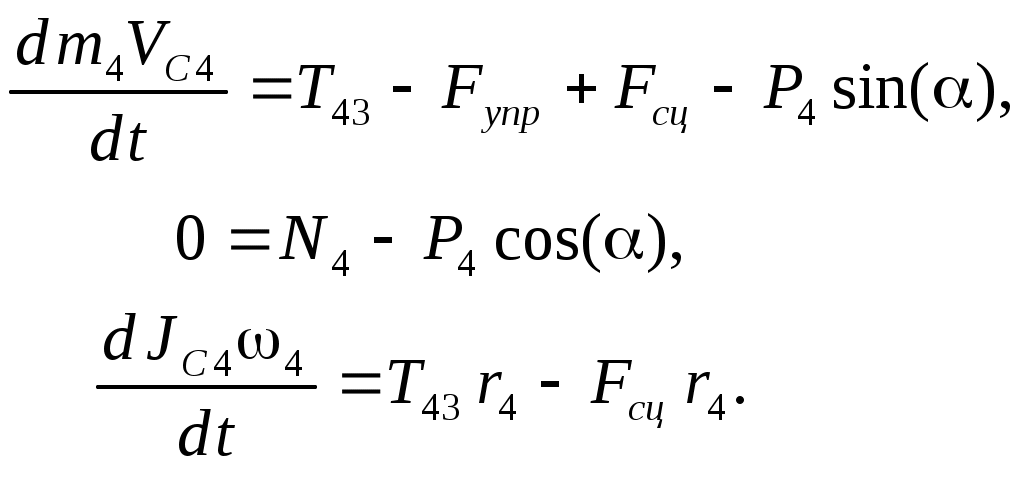 | (Определение реакций внешних и внутренних связей..0) |
С учетом кинематических соотношений (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) систему уравнений (Определение реакций внешних и внутренних связей..0) – (Определение реакций внешних и внутренних связей..0) преобразуем к виду:
| | (Определение реакций внешних и внутренних связей..0) |
Уравнения (Определение реакций внешних и внутренних связей..0) составляют систему алгебраических уравнений относительно функций
4.С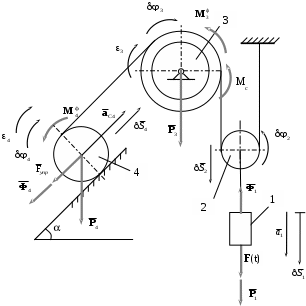 оставление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа.
оставление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа.
-
Расчетная схема.
Общее уравнение динамики системы есть математическое выражение принципа Даламбера-Лагранжа
| | | (Составление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа..0) |
Здесь
Изобразим на рисунке активные силы и силы инерции (рис. 4).
Сообщим системе возможное перемещение. Возможная работа активных сил определяется как сумма следующих элементарных работ:
| | | (Составление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа..0) |
Сумма элементарных работ указанных сил вычисляется, как и мощность по формуле (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0)
| | 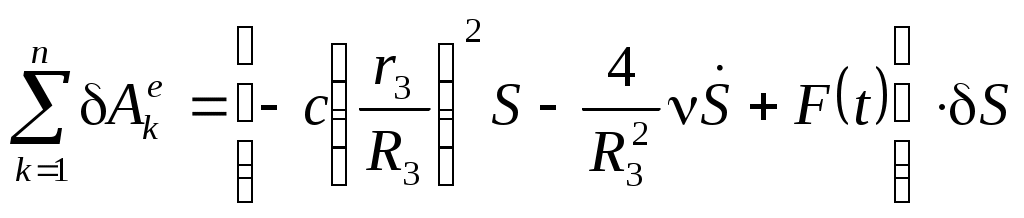 | (Составление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа..0) |