Файл: Курсовая работа по динамике исследование колебаний механической системы с одной степенью свободы.doc

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИИФГБОУ ВПО ТУЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТКафедра теоретической механикиКУРСОВАЯ РАБОТА ПО ДИНАМИКЕ«ИССЛЕДОВАНИЕ КОЛЕБАНИЙ МЕХАНИЧЕСКОЙ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ»Выполнил: Вдовин СергейРуководитель: Ткач О.А.Тула, 2022

ОГЛАВЛЕНИЕ

	Аннотация	3
	Схема механизма и данные для выполнения задания	4
1	Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы	7
2	Определение закона движения системы	10
3	Определение реакций внешних и внутренних связей	13
4	Составление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа	15
5	Составление дифференциального уравнения движения механизма с помощью уравнений Лагранжа 2-го рода	17
6	Построение алгоритма вычислений	19
	Результаты вычислений	22
	Выводы	26
	Литература	27

Аннотация.

---

Исследуется движение механической системы с одной степенью свободы, на которую действуют момент сопротивления и возмущающая гармоническая сила F(t) Трением качения и скольжения следует пренебречь. Качение катков происходит без скольжения, проскальзывание нитей на блоках отсутствует. Требуется, используя основные теоремы динамики системы и аналитические методы теоретической механики, определить закон движения первого тела и реакции внешних и внутренних связей.Схема механизма и данные для выполнения задания

1. 
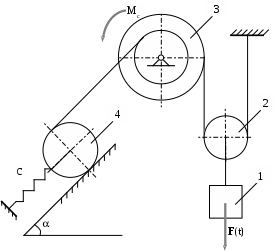
   Схема механизма.
   

Дано:

m1 = 1 кг	r2 = 0,1 м	m = 1,5 кг/с	s0 = 0,09 м
m2 = 0	r3 = 0,2 м	 = 1,25 Н м с	v0 = 0
m3 = 2 кг	R3 = 0,3 м	c = 4000 Н/м	 = 45o
m4 = 3 кг	i3 = 0,3 м	fсц = 0,10
	r4 = 0,15 м	F0 = 50 Н
	i4 = 0,15 м (*)	p =  рад/с

* – однородный сплошной цилиндр радиуса «r_k».

---

1.Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы.

Изобразим расчетную схему (рис. 2.)

2. 
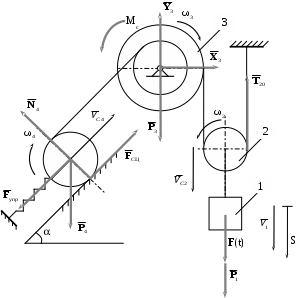
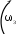
   Расчетная схема.
   

На рис. 2 обозначено: – силы тяжести, –нормальная реакция опорной плоскости, – сила натяжения нити, – упругая реакция пружины, – сила сцепления катка с опорной плоскостью, – реакции подшипника блока 3, – момент вязкого сопротивления, – возмущающая сила.Рассматриваемая механическая система имеет одну степень свободы. Будем определять положение системы с помощью координаты . Начало отсчета координат совместим с положением статического равновесия груза 1. Для построения дифференциального уравнения движения системы используем теорему об изменении кинетической энергии механической системы в форме:

,

(Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0)

где обозначено:Т – кинетическая энергия системы, – сумма мощностей внешних сил,

---

– сумма мощностей внутренних сил.

Вычислим кинетическую энергию системы как сумму кинетических энергий тел, образующих механическую систему.

Груз 1 совершает поступательное движение. Его кинетическая энергия равна:

(Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0)

Блок 2 и каток 4 совершают плоскопараллельное движение, поэтому

(Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0)

где – момент инерции катка 4. Поскольку блок 2 считаем невесомым, его кинетическая энергия равна нулю. Блок 3 совершает вращательное движение около неподвижной оси. Его кинетическая энергия определяется по формуле:

(Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0)

где – момент инерции блока 3. Кинетическая энергия всего механизма будет равна:

(Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0)

Так как система имеет одну степень свободы и в качестве координаты, определяющей ее положение, ранее принято перемещение груза 1, то кинематические характеристики всех тел механизма легко выражаются через кинематические параметры груза 1 соотношениями:

---

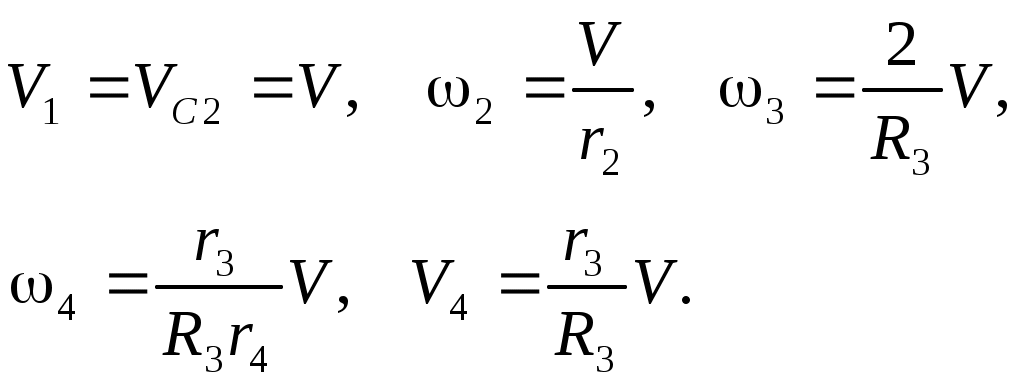(Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0)

Подставляя (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0), (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0), (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) в (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) с учетом (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0), окончательно получаем:

			(Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0)
где		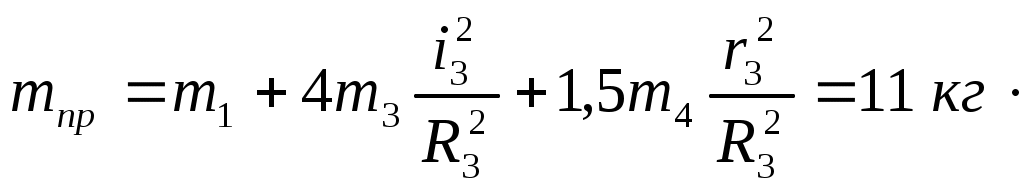	(Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0)

называется приведенной массой. Теперь вычислим правую часть уравнения (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) – сумму мощностей внешних и внутренних сил. Мощность силы равна скалярному произведению вектора силы на скорость точки приложения силы, а мощность момента силы – алгебраическому произведению момента силы на угловую скорость вращения тела, к которому приложен момент: Знак "+" берется в том случае

---