Файл: Курсовая работа по динамике исследование колебаний механической системы с одной степенью свободы.doc
Добавлен: 12.12.2023
Просмотров: 191
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2.Определение закона движения системы.
3.Определение реакций внешних и внутренних связей.
4.С оставление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа.
5.Составление дифференциального уравнения движения механизма с помощью уравнения Лагранжа 2-го рода.
6.ПОСТРОЕНИЕ АЛГОРИТМА ВЫЧИСЛЕНИЙ
, если направления момента и угловой скорости одинаковы, а знак "–" если их направления противоположны.
Рассматриваемая нами механическая система является неизменяемой, т.е. тела, входящие в систему, не деформируемы и скорости их точек относительно друг друга равны нулю. Поэтому мощности внутренних сил будут равняться нулю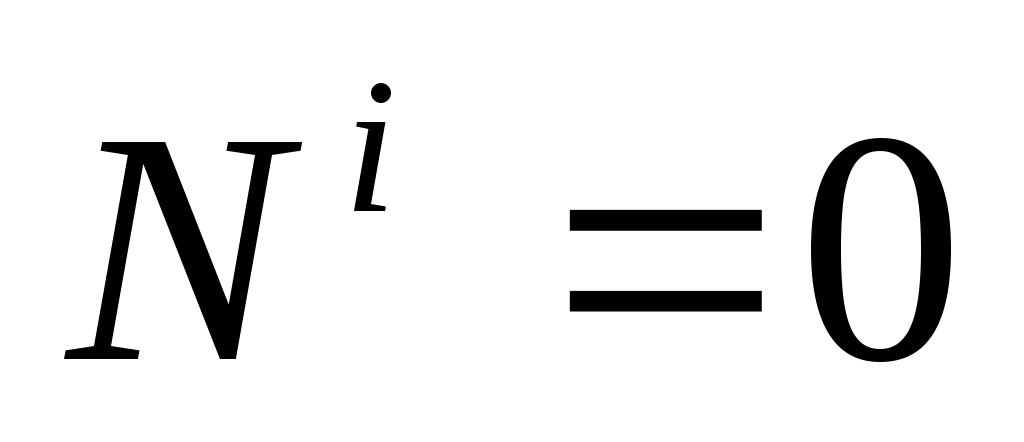 .
.
Будут равняться нулю и мощности некоторых внешних сил, приложенных в точках, скорости которых равны нулю. Как видно из расчетной схемы, таковыми являются силы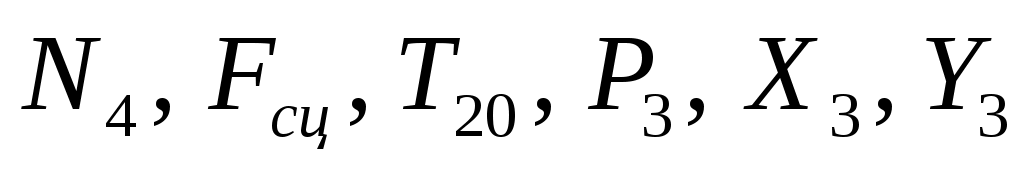
Сумма мощностей остальных сил равна:
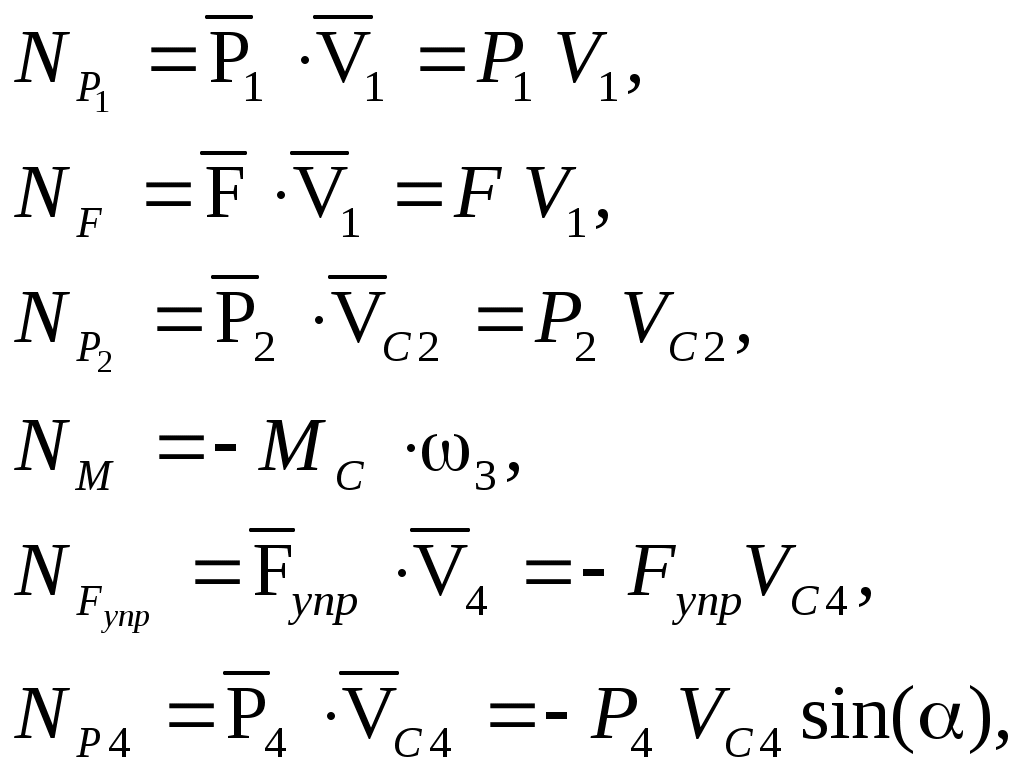
или
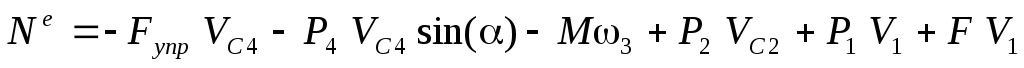 .
.
С учетом кинематических соотношений (1.6) сумму мощностей внешних сил преобразуем к виду:
называется приведенной силой.
Упругую силу считаем пропорциональной удлинению пружины. Полное удлинение пружины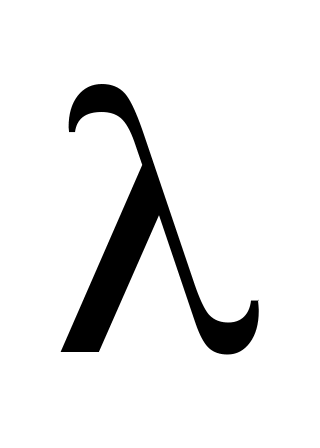 равно сумме статического
равно сумме статического 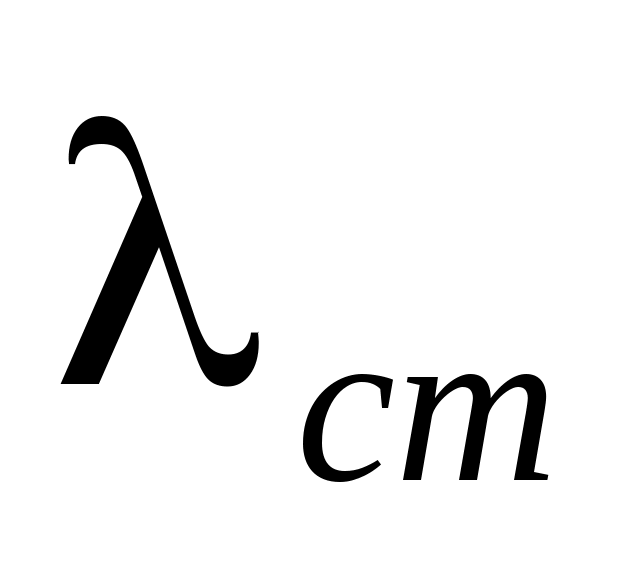 и динамического
и динамического 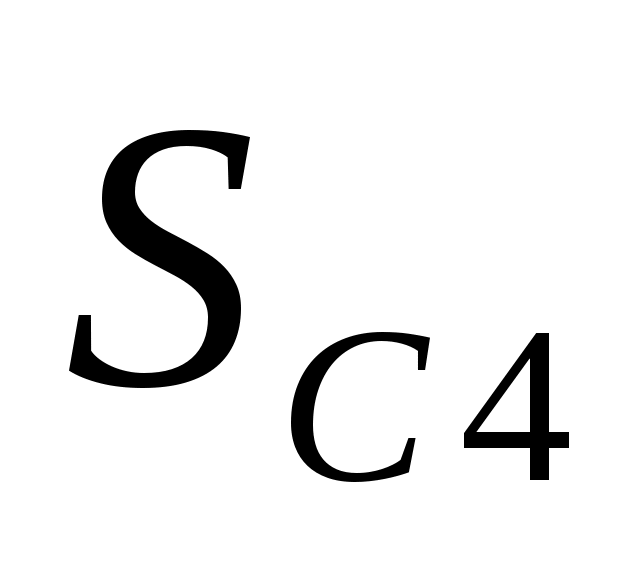 удлинений
удлинений
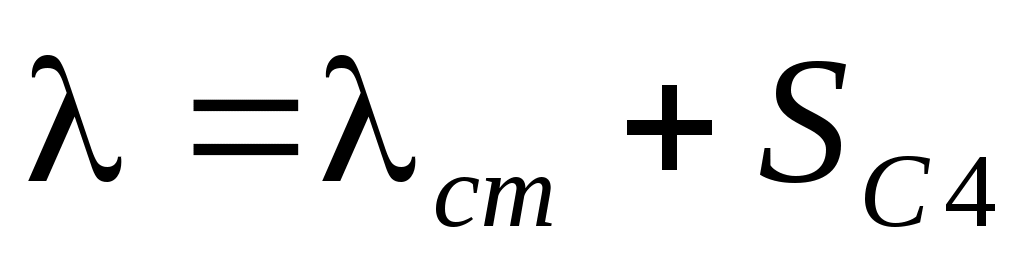 .
.
Тогда упругая сила будет равна:
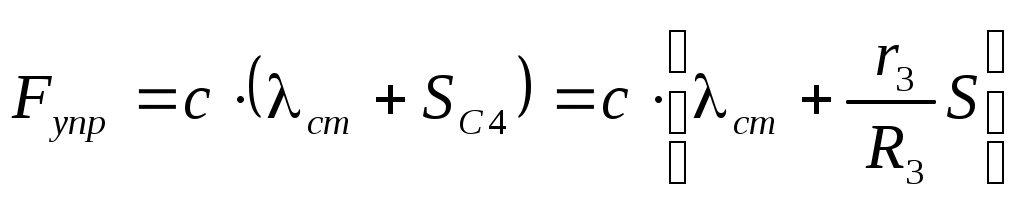 .
.
Момент вязкого сопротивления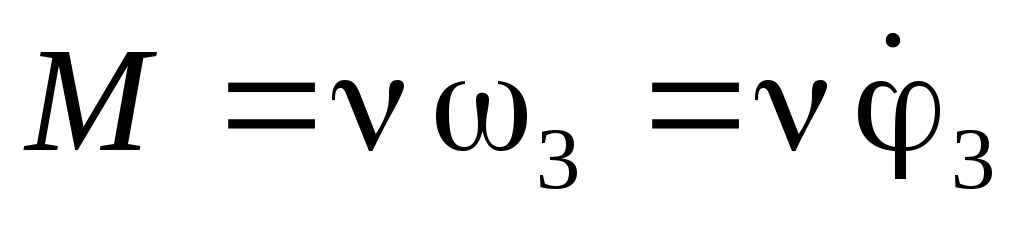 . Тогда приведенная сила (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) в развернутой форме будет определяться выражением:
. Тогда приведенная сила (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) в развернутой форме будет определяться выражением:
В состоянии покоя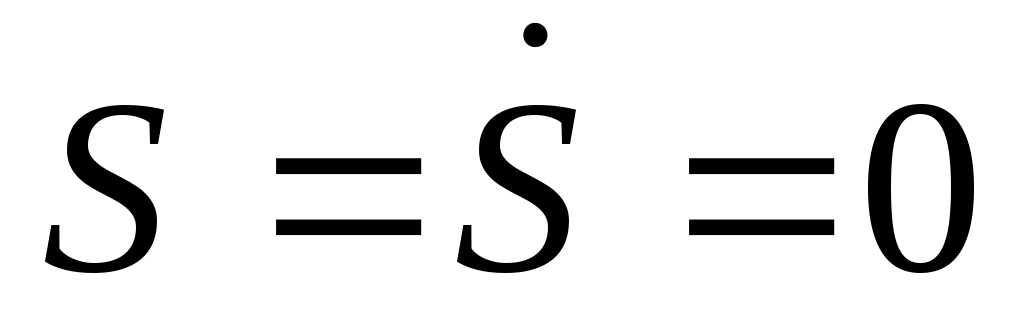 и условиемравновесия системы будет служить уравнение
и условиемравновесия системы будет служить уравнение
Из уравнения (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) определяется статическое удлинение пружины
Таким образом, окончательное выражение для приведенной силы (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) будет иметь вид:
Подставим выражения для кинетической энергии (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) и сумму мощностей всех сил (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0)с учетом (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) в уравнение (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0). Тогда, после дифференцирования, получаем дифференциальное уравнение движения системы:
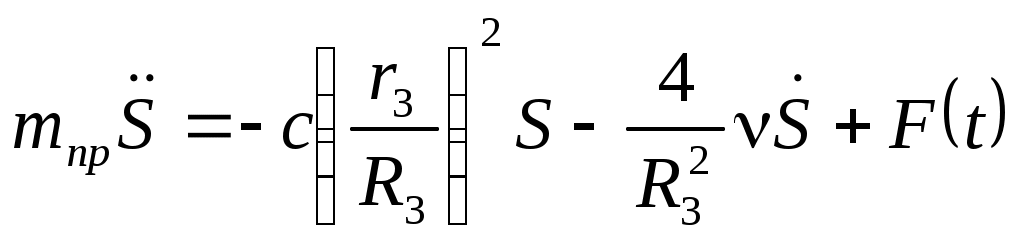
Общепринято такие уравнения представлять в виде:
где введены коэффициенты, имеющие определенный физический смысл:
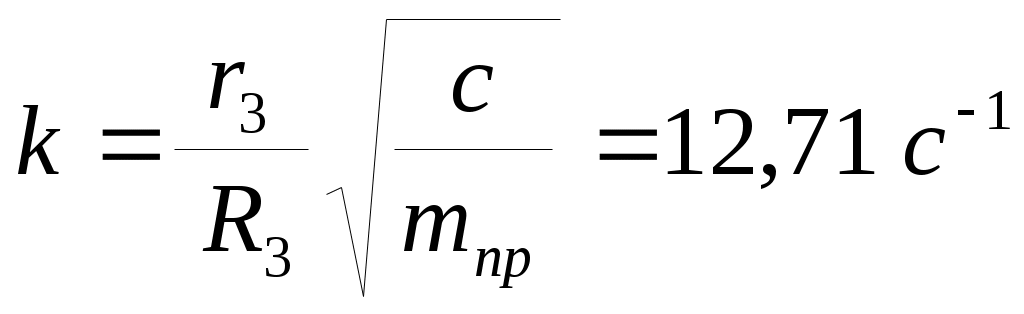 – частота собственных колебаний,
– частота собственных колебаний,
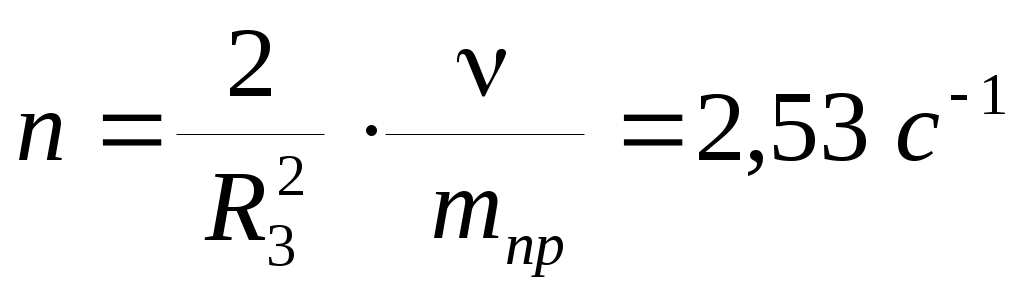 – показатель степени затухания колебаний.
– показатель степени затухания колебаний.
Начальные условия:
Уравнения (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0), (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) представляют математическую модель для решения второй задачи динамики.
Возмущающая сила изменяется по гармоническому закону:
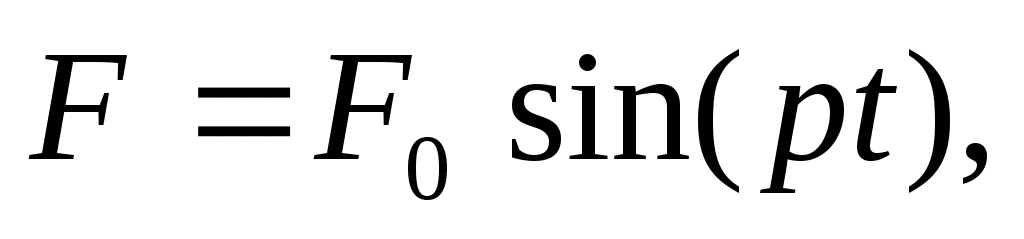
где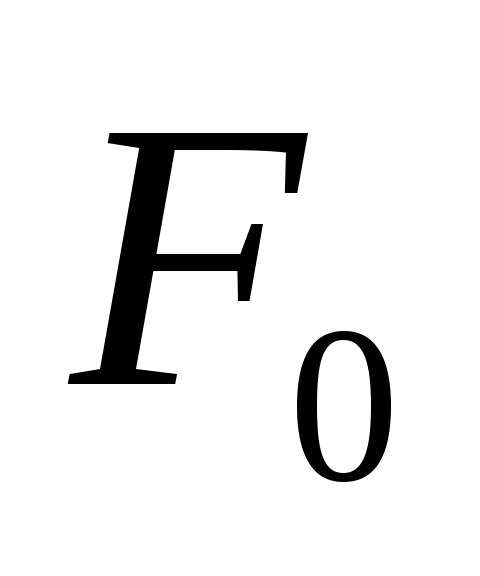 – амплитуда возмущающей силы,
– амплитуда возмущающей силы, 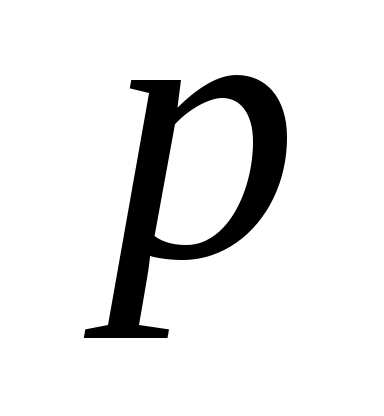 – циклическая частота возмущения.
– циклическая частота возмущения.
Дифференциальное уравнение движения механической системы (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) с учетом выражения для возмущающей силы примет вид:
где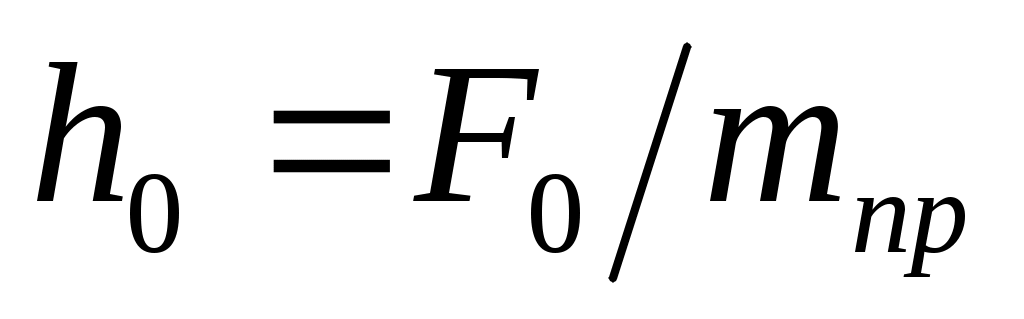 .
.
Общее решение неоднородного дифференциального уравнения (Определение закона движения системы..0) складывается из общего решения однородного уравнения и частного решения неоднородного. Однородное дифференциальное уравнение, соответствующее неоднородному уравнению (Определение закона движения системы..0), имеет вид:
Решение этого уравнения ищем в виде функции
где и
и 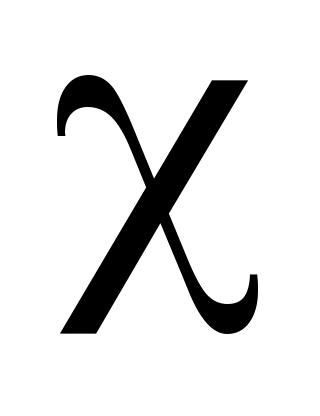 – неопределенные постоянные величины.
– неопределенные постоянные величины.
Подставляя (Определение закона движения системы..0) в (Определение закона движения системы..0), получим:
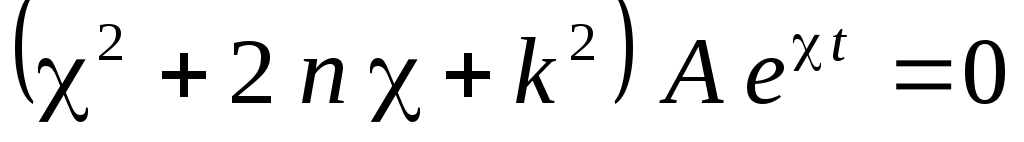
Так как мы ищем нетривиальное решение, то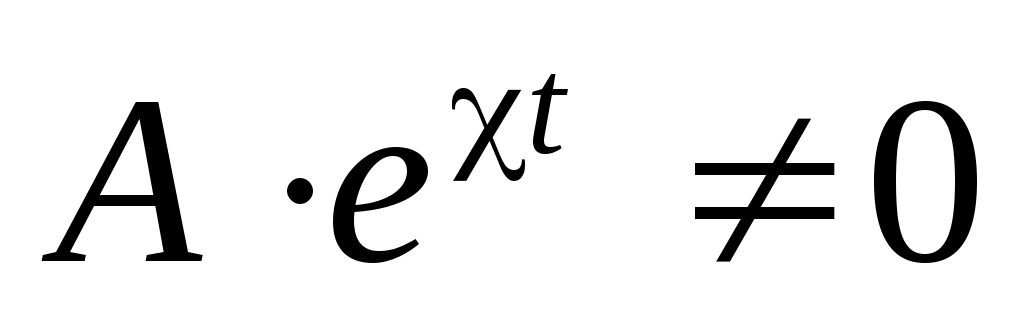 . Следовательно, должно выполняться условие
. Следовательно, должно выполняться условие
Уравнение (Определение закона движения системы..0) называется характеристическим уравнением дифференциального уравнения (Определение закона движения системы..0). Это уравнение имеет два корня:
где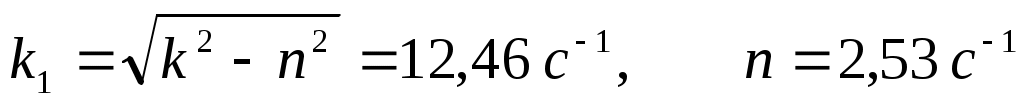 .
.
В этом случае (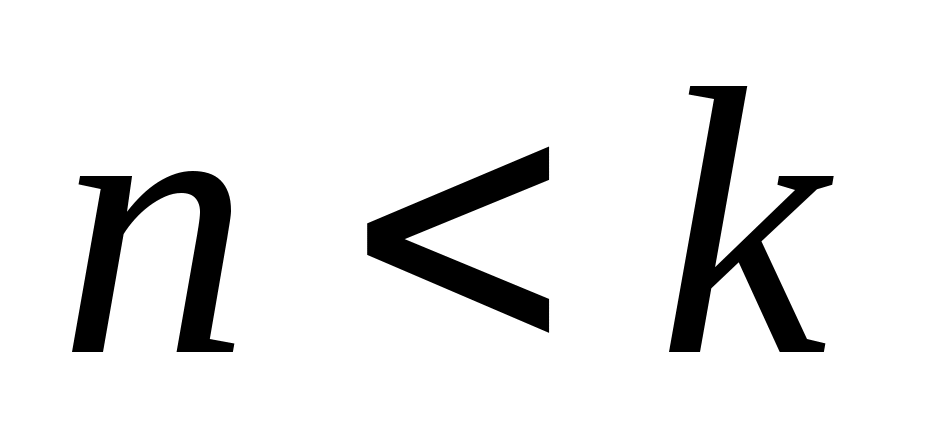 ) общее решение уравнения (2.2) имеет вид:
) общее решение уравнения (2.2) имеет вид:
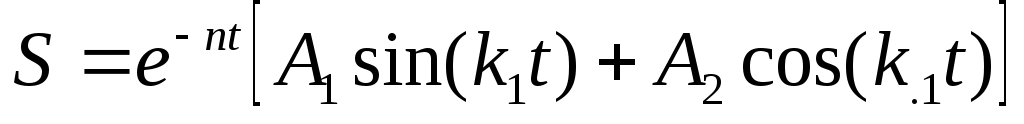
Данное выражение нетрудно представить в виде
где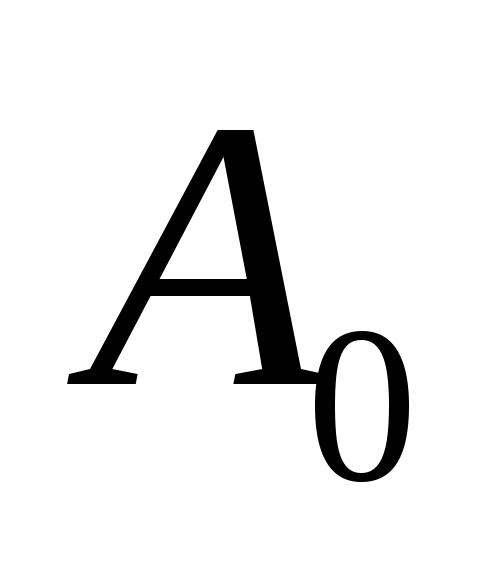 ,
, 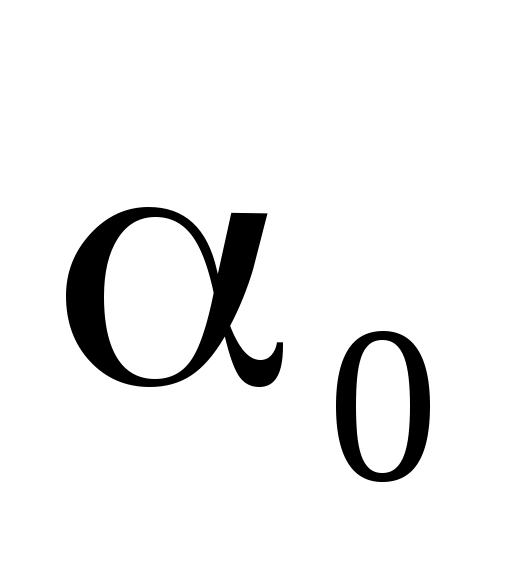 – постоянные интегрирования.
– постоянные интегрирования.
Определим частное решение неоднородного дифференциального уравнения (Определение закона движения системы..0). Частное решение ищем в виде правой части
где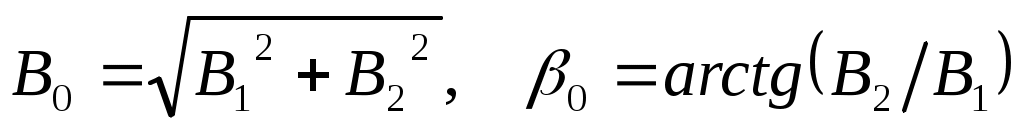
Рассматриваемая нами механическая система является неизменяемой, т.е. тела, входящие в систему, не деформируемы и скорости их точек относительно друг друга равны нулю. Поэтому мощности внутренних сил будут равняться нулю
Будут равняться нулю и мощности некоторых внешних сил, приложенных в точках, скорости которых равны нулю. Как видно из расчетной схемы, таковыми являются силы
Сумма мощностей остальных сил равна:
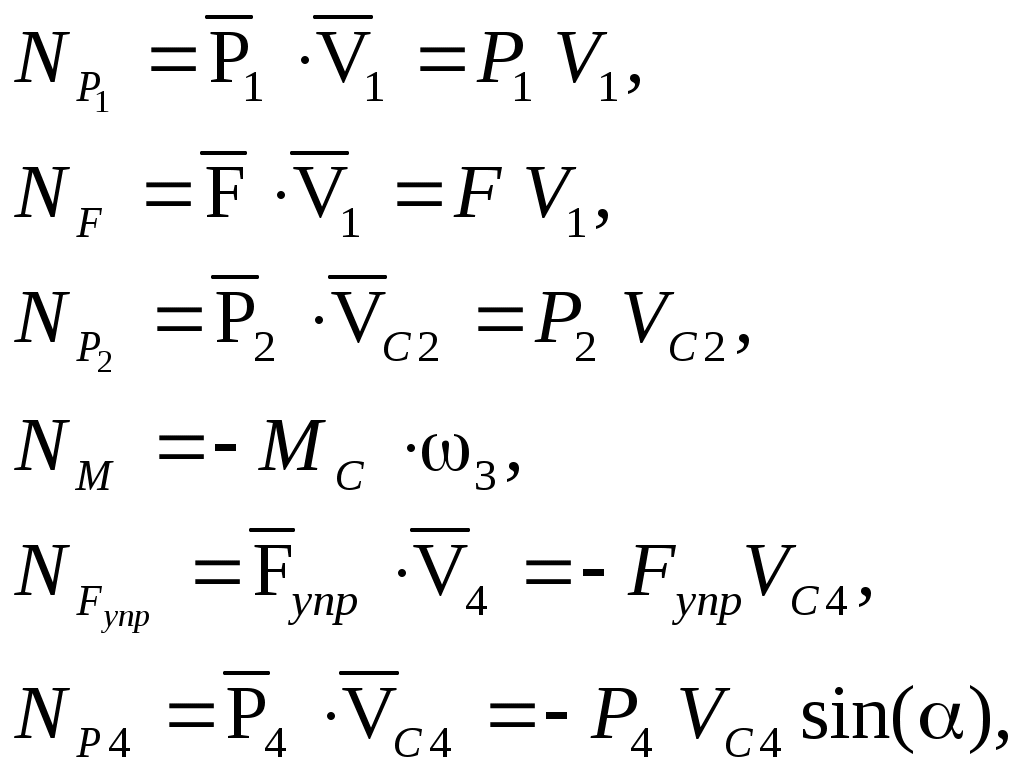
или
С учетом кинематических соотношений (1.6) сумму мощностей внешних сил преобразуем к виду:
| | | (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) |
| где | | (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) |
называется приведенной силой.
Упругую силу считаем пропорциональной удлинению пружины. Полное удлинение пружины
Тогда упругая сила будет равна:
Момент вязкого сопротивления
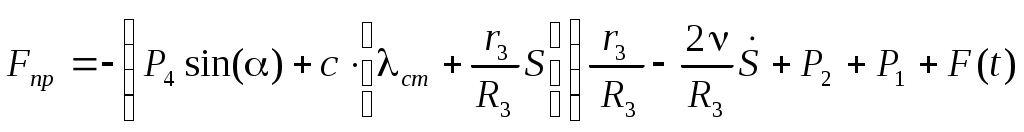 . . | (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) |
В состоянии покоя
| | | (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) |
Из уравнения (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) определяется статическое удлинение пружины
| | | (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) |
Таким образом, окончательное выражение для приведенной силы (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) будет иметь вид:
| | 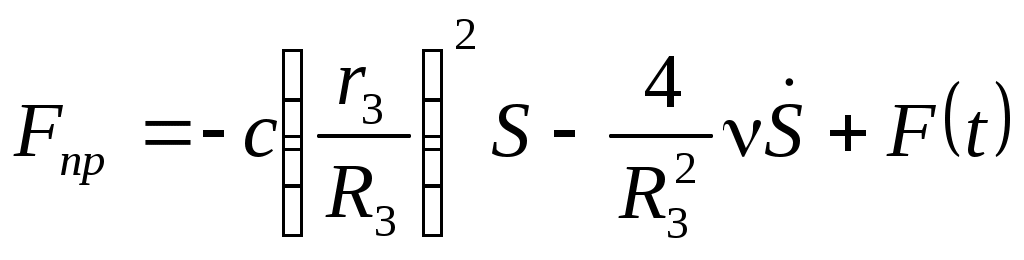 | (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) |
Подставим выражения для кинетической энергии (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) и сумму мощностей всех сил (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0)с учетом (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) в уравнение (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0). Тогда, после дифференцирования, получаем дифференциальное уравнение движения системы:
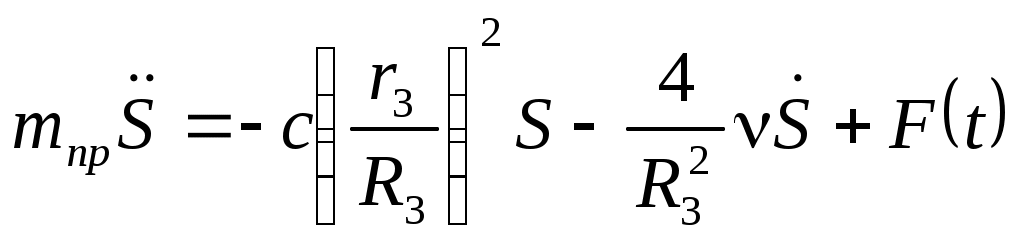
Общепринято такие уравнения представлять в виде:
| | | (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) |
где введены коэффициенты, имеющие определенный физический смысл:
Начальные условия:
| | при | (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) |
Уравнения (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0), (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) представляют математическую модель для решения второй задачи динамики.
2.Определение закона движения системы.
Возмущающая сила изменяется по гармоническому закону:
где
Дифференциальное уравнение движения механической системы (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) с учетом выражения для возмущающей силы примет вид:
| | | (Определение закона движения системы..0) |
где
Общее решение неоднородного дифференциального уравнения (Определение закона движения системы..0) складывается из общего решения однородного уравнения и частного решения неоднородного. Однородное дифференциальное уравнение, соответствующее неоднородному уравнению (Определение закона движения системы..0), имеет вид:
| | | (Определение закона движения системы..0) |
Решение этого уравнения ищем в виде функции
| | | (Определение закона движения системы..0) |
где
Подставляя (Определение закона движения системы..0) в (Определение закона движения системы..0), получим:
Так как мы ищем нетривиальное решение, то
| | | (Определение закона движения системы..0) |
Уравнение (Определение закона движения системы..0) называется характеристическим уравнением дифференциального уравнения (Определение закона движения системы..0). Это уравнение имеет два корня:
| | | (Определение закона движения системы..0) |
где
В этом случае (
Данное выражение нетрудно представить в виде
| | | (Определение закона движения системы..0) |
где
Определим частное решение неоднородного дифференциального уравнения (Определение закона движения системы..0). Частное решение ищем в виде правой части
| | | (Определение закона движения системы..0) |
где