ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 518
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- высокая нагрузочная способность (до N=50000 кВт);
- высокий КПД (до 0,97-0,99 для одной пары колес);
- большая надежность в работе, простота обслуживания;
К недостаткам зубчатых передачследует отнести:
- невозможность бесступенчатого изменения передаточного числа;
- высокие требования к точности изготовления и монтажа;
- шум при больших скоростях; плохие амортизирующие свойства;
- высокая жесткость, не позволяющая компенсировать динамические нагрузки;
Основные элементы зубчатой передачи.
Одноступенчатая зубчатая передача состоит из двух зубчатых колес - ведущего и ведомого. Меньшее по числу зубьев из пары колес называют шестерней, а большее колесом. Зубчатое зацепление характеризуется следующими основными параметрами:
da— диаметр вершин зубьев;
dr— диаметр впадин зубьев;
da— начальный диаметр;
d — делительный диаметр;
рt— окружной шаг;
h — высота зуба;
ha— высота ножки зуба;
с — радиальный зазор;
b — ширина венца (длина зуба);
еt — окружная ширина впадины зуба;
st— окружная толщина зуба;
a???? — межосевое расстояние;
а — делительное межосевое расстояние;
Z — число зубьев.
Делительная окружность - окружность, по которой обкатывается инструмент при нарезании. Делительная окружность связана с колесом и делит зуб на головку и ножку.
Основные элементы зубчатых колес представлены на рис.15.
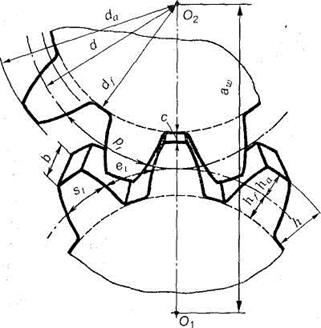
Рис. 15. Геометрические параметры цилиндрических зубчатых колес
Модулем зубьев т называется часть диаметра делительной окружности, приходящаяся на один зуб.
Модуль является основной характеристикой размеров зубьев. Для пары зацепляющихся колес модуль должен быть одинаковым.
Линейную величину, в ???? раз меньшую окружного шага зубьев, называют окружным модулем зубьев и обозначают т:
Размеры цилиндрических прямозубых колес вычисляют по окружному модулю, который называют расчетным модулем зубчатого колеса, или просто модулем; обозначают буквой т. Модуль измеряют в миллиметрах. Модули стандартизованы (табл. 3).
Таблица 3. Стандартные значения модулей
| 1-й ряд | 2-й ряд | 1-й ряд | 2-й ряд | 1-й ряд | 2-й ряд | 1-й ряд | 2-й ряд |
| 1 | 1,125 | 3 | 3,5 | 10 | 11 | 32 | 36 |
| 1,25 | 1,375 | 4 | 4,5 | 12 | 14 | 40 | 45 |
| 1,5 | 1,75 | 5 | 5,5 | 16 | 18 | 50 | 55 |
| 2 | 2,25 | 6 | 7 | 20 | 22 | 60 | 70 |
| 2,5 | 2,75 | 8 | 9 | 25 | 28 | 80 | 90 |
Примечание. При назначении модулей первый ряд значений следует предпочитать второму.
Основная теорема зубчатого зацепления.
Пусть имеется пара зубчатых колес с центрами О1и О2,вращающихся соответственно с угловыми скоростями и На рис.18, а показаны сложения, которые последовательно занимает пара сопряженных (эвольвентных) зубьев в процессе их зацепления; прямую О1О2называют межосевой линией зубчатой передачи. Проведем в точках касания зубьев К1, К2, К3, ... общие нормали к профилям. Все эти нормали NN должны пересекать межосевую линию О1О2в постоянной точке Р. Эту точку называют полюсом зацепления;ее положение на межосевой линииопределяется отношением угловых скоростей колес, т.е. их отношением:
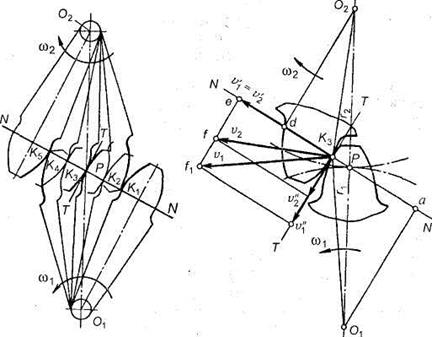
а)б)
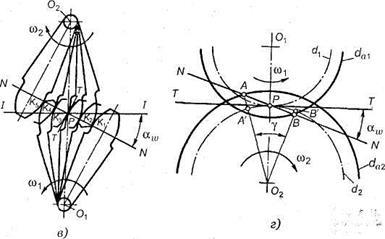
Рис. 18. Элементы зубчатого зацепления
Основную теорему зацепленияможно сформулировать так: общая нормаль к профилям зубьев в точке их касания пересекает межосевую линию в точке Р, называемой полюсом зацепления и делящей межосевое расстояние на отрезки, обратно пропорционально угловым скоростям.
Следствие: для обеспечения постоянного передаточного отношения положение полюса Р на линии центров должно быть постоянным.
В процессе работы сопряженных (эвольвентных) профилей точка их касания все время перемещается по прямой NN. Эту прямую называют линией зацепления.
Место (точку) входа в зацепление и выхода из него сопряженных зубьев можно определить при следующем геометрическом построении.
Длина линии зацепления qa— отрезок линии зацепления, отсекаемый окружностями вершин зубьев сопряженных колес. Он определяет начало иконец зацепления пары сопряженных зубьев. Длина зацепления — активная часть линии зацепления.
Коэффициент торцового перекрытия — отношение длины линии зацепления к шагу:
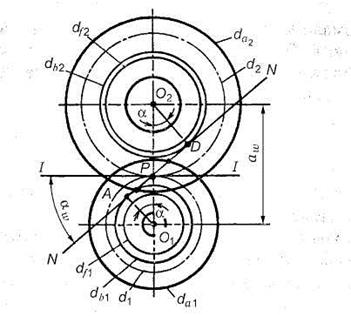
Рис. 19. Геометрические параметры зубчатой передачи
В современном машиностроении для построения сопряженных профилей применяют ограниченное число кривых.
Профили зубьев должны быть технологичными, т.е. такими, чтобы их можно было получить в производственных условиях наиболее простыми методами. Из теоретически возможных профилей преимущественное применение получили эвольвентные профили(см. рис. 18, б). Это обусловлено тем, что эвольвентное зацепление, будучи достаточно простым геометрически, имеет существенные технологические и эксплуатационные преимущества: эвольвентные зубья могут быть весьма точно нарезаны относительно простым инструментом с прямолинейными режущими кромками, причем одним инструментом можно нарезать колеса с различным числом зубьев; эвольвентные передачи нечувствительны к отклонениям межосевого расстояния от его теоретического значения; они допускают модификацию профиля зубьев, сводящуюся к выбору оптимальных участков эвольвенты, обеспечивающих наилучшие работоспособность, к.п.д. и другие. Это зацепление может быть использовано и в сменных колесах. Эвольвентное зацепление предложено Эйлером более 200 лет назад в 1760 г.
В зацеплении М.Л. Новикова, предложенном в 1954 г., рабочие профили зубьев очерчены дугами окружностей (рис. 20, 21). Передачи Новикова имеют повышенную (в 1,5...2 раза), по сравнению с эвольвентными, контактную несущую способность, но пониженную изгибную выносливость. Ввиду сложности изготовления и монтажа передачи с зацеплением Новикова пока нашли применение только в специальном машиностроении.
Рис. 20. Колесо с зацеплением М. Л. Новикова
Краткие сведения о корригировании зацеплений
Форма эвольвентного профиля зубьев при заданном угле инструмента и модуле зависит от числа зубьев