Файл: Пинигина Дарья Леонидовна задание задача 1 Пассажир может уехать на любом из двух маршрутов автобусов закон.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 75
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задача №3
1.1
Исходные данные и отформатированная для удобства выборка предоставлены в Приложении 1, т.к. очень объемны.
1.1.1
Максимальное и минимальное значение выборки:
По правилу Стёрджеса определим количество интервалов, на которые мы разобьём интервал с границами
Рассмотрим выборку через интервальный вариационный ряд по
Рассчитаем в таблице 3.1 начало и конец интервала:
Таблица 3.1 интервальный вариационный ряд
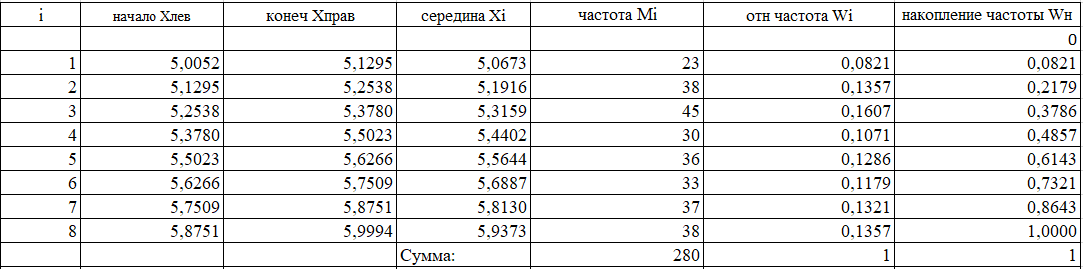
1.1.2 Графическое представление выборки
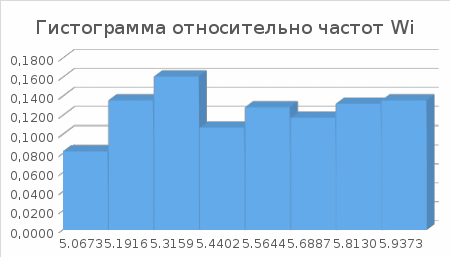
Рис. 3.1 Гистограмма относительных частот
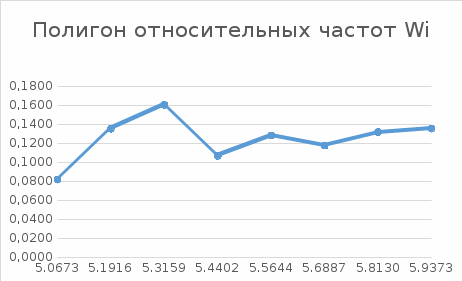
Рис. 3.2 Полигон относительных частот
Остальные графики приведены в Приложении 1.
1.1.3 Описательные характеристики [5]:
-
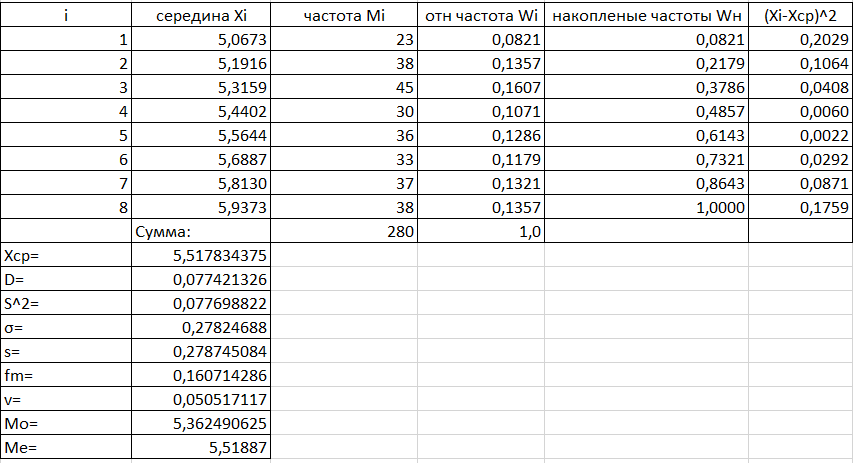
Выборочное среднее значение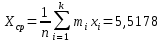
-
Выборочная дисперсия: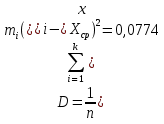
-
Несмещенная (исправленная) оценка дисперсии: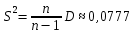
-
Выборочное среднеквадратичное отклонение: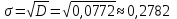
-
Стандартное отклонение выборки: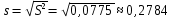
-
Модальный интервал: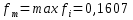
-
Коэффициент вариации: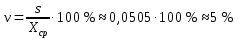
-
Мода: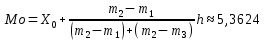
-
Медиана: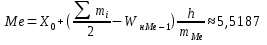
Таблица 3.2 Расчёт описательных характеристик
1.2.
Гипотеза о законе распределения СВ
Мода, медиана и выборочное среднее значение близки.
Применяя в качестве нулевой гипотезу Ho: генеральная совокупность, из которой извлечена выборка, имеет не равномерное распределение. Тогда H1: совокупность, из которой извлечена выборка, имеет равномерное распределение.
Построим график эмпирической функции поверх теоретического графика равномерного распределения:
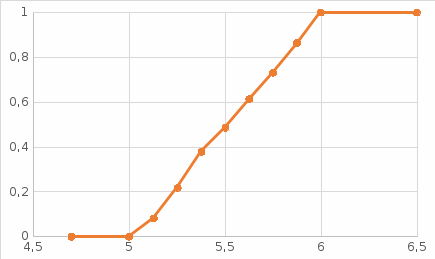
Рис 3.3 график эмпирической функции поверх теоретического графика равномерного распределения
Из графика видно , что они схожи.
Найдем оценки параметров равномерного распределения:
Найдем плотность равномерного распределения:
Найдем теоритические частоты
Применим критерий согласия Пирсона:
Проверим гипотезу о распределении наблюдаемой случайной величины на 5% уровне значимости по хи-квадрат
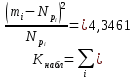
Таблица 3.3 Гипотеза о равномерном распределении
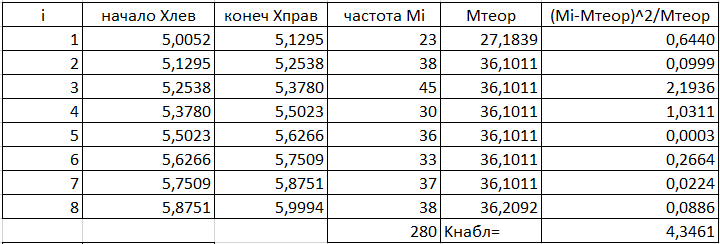
Для уровня значимости
Для уровня значимости
1.3.1. Определение погрешности
При определении среднего, если воспользоваться несгруппированными данными получим:
Различие со значением по группированным данным:
1.3.2. Построить 95% доверительные интервалы для параметров (параметра) «теоретического» распределения.
2. Проверка статистических гипотез [8]
1) Проверим гипотезу о соответствии нормального распределения
Используем критерий согласия Пирсона:
Таблица 3.4 нормальное распределение
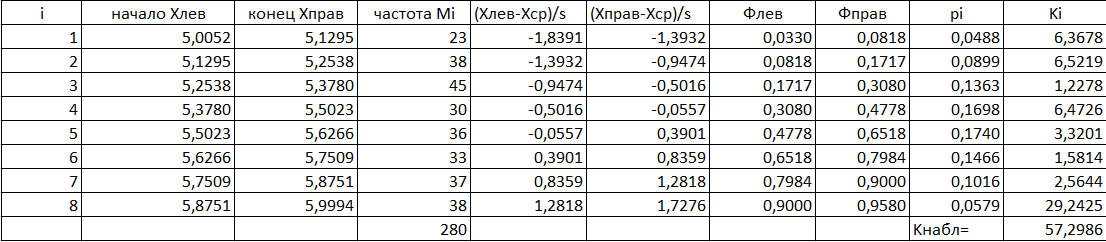
Проверим гипотезу о распределении наблюдаемой случайной величины на 5% уровне значимости по критерию хи-квадрат
Для уровня значимости
2) Проверим гипотезу генеральное среднее
H0: генеральное среднее
H1: генеральное среднее
Определим критическое значение по таблице функции Лапласа:
3) Проверим гипотезу что случайная величина распределена по закону Пуассона
Вероятность попадания в i-й интервал случайной величины, распределённой по гипотетическому закону:
Примем в качестве оценки параметра
Отсюда
Таблица 3.5 Распределение Пуссона
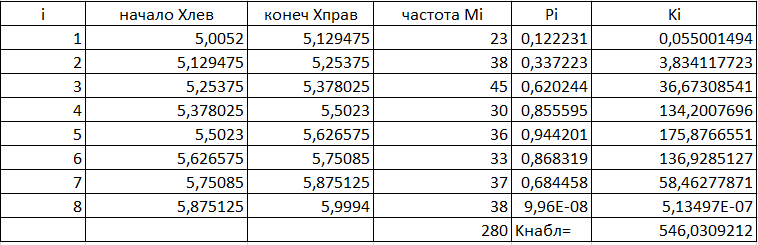
Проверим гипотезу о распределении наблюдаемой случайной величины на 5% уровне значимости по критерию хи-квадрат
Для уровня значимости
3.
Таблица 3.6 для вычисления пункта 3
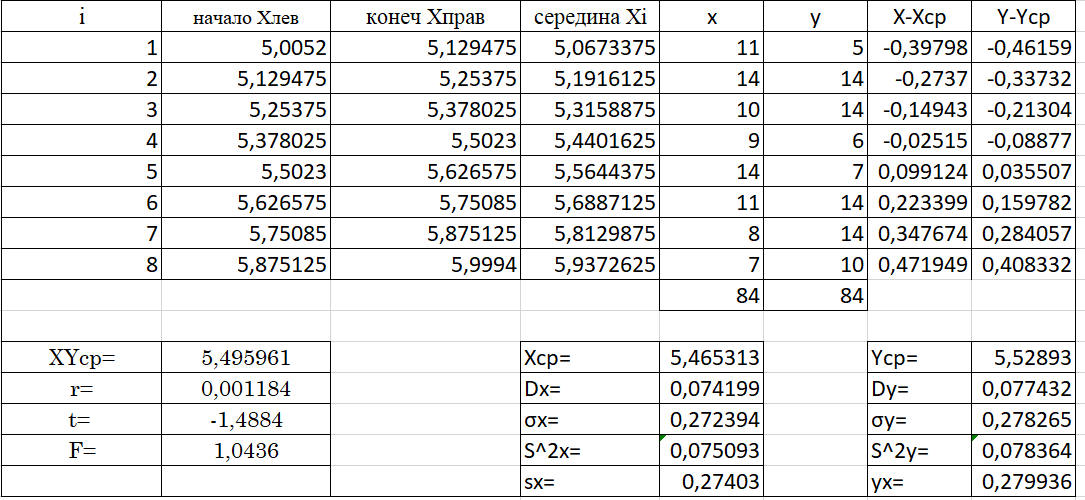
3.1. Гипотеза об однородности
Выдвинем гипотезу, что рассматриваемые выборки однородны. Воспользуемся критерием Фишера:
Критическое значение F для степеней свободы k1 = k2 = n – 1 = 83:
Значит, что выборки однородны, отсюда можно сделать вывод что рассматриваемые выборки извлечены из одной и той же генеральной совокупности.
3.2. Гипотеза о равенстве средних [8]
Выдвинем гипотезу Xср = Yср.
Воспользуемся t-критерием Стьюдента:
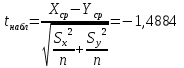
Критическое значение по таблице для m = 2n – 1 = 167,