Файл: Пинигина Дарья Леонидовна задание задача 1 Пассажир может уехать на любом из двух маршрутов автобусов закон.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 77
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| | | | | | | |
| 1 | 1 | 0,38 | | 1 | 2 | 0,19 |
| 2 | 3 | 0,35 | | 2 | 5 | 0,29 |
| 3 | 7 | 0,27 | | 3 | 8 | 0,23 |
| | | | | 4 | 11 | 0,29 |
Математические ожидания случайных величин
Дисперсии случайных величин
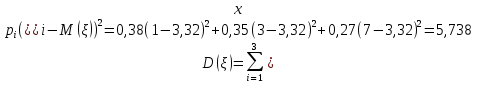
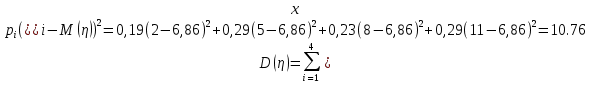
Среднеквадратическое отклонение случайных величин
Совместная функция распределения дискретной двухмерной случайной велечины (
Таблица 2.4 Совместная функция распределения дискретной двухмерной случайной велечины (
| | y1 | y2 | y3 | y4 |
| x1 | 0,1 | 0,11 + 0,1 = 0,21 | 0,07 + 0,21 = 0,28 | 0,1 + 0,29 = 0,38 |
| x2 | 0,08 + 0,38 = 0,46 | 0,11 + 0,46 = 0,57 | 0,05 + 0,57 = 0,62 | 0,11 + 0,62 = 0,73 |
| x3 | 0,00 + 0,73 = 0,73 | 0,08 + 0,73 = 0,81 | 0,11 + 0,81 = 0,92 | 0,08 + 0,92 = 1 |
Рис 2.1 График совместная функция распределения дискретной двухмерной случайной велечины (
1.2
Условный закон распределения случайной величины
Таблица 2.5. Условный закон распределения
| | | | | |
| | | 1 | 3 | 7 |
| | 2 | | | 0 |
| | 5 | | | |
| | 8 | | | |
| | 11 | | | |
Условное математическое ожидание:
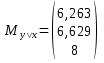
Условная дисперсия:
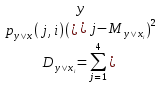
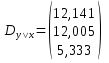
Условное среднеквадратичное отклонение:
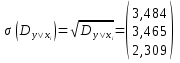
1.3
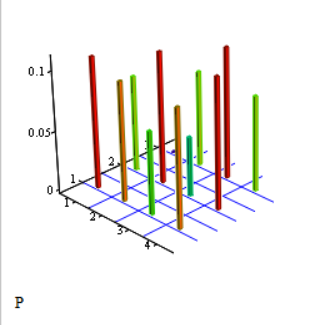
Рис 2.2 Графическое изображение совместного закона распределения двухмерной СВ в виде диаграммы рассеивания
1.4
Ковариация случайной величины
Коэффициент корреляции (линейный) случайной величины
Корреляционное отношение:
Функция линейной регрессии:
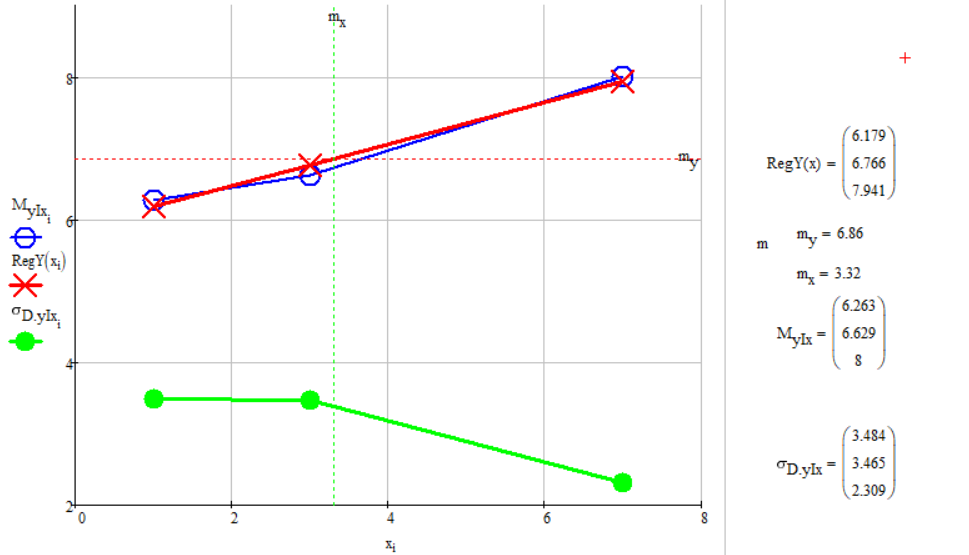
Рис 2.3 График функции линейной регрессии, условного математического ожидания, условного среднеквадратичного отклонения.
Вывод:
Ковариация случайной величины
Мы определили степень связи случайных величин по средствам вычисления генерального корреляционного отношения 0,1< ρ= 0,217 < 0,3 , значит, связь между величинами (по шкале Чеддока) слабая.