Файл: Пинигина Дарья Леонидовна задание задача 1 Пассажир может уехать на любом из двух маршрутов автобусов закон.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 72
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра Вычислительной техники
Расчётно-графическая работа
По дисциплине
«Теория вероятности и математическая статистика»
Тема: Анализ вероятностных свойств одномерных и двухмерных случайных величин средствами теории вероятностей и математической статистики.
Вариант 4
| Факультет: АВТФ Группа: Студент: | Преподаватель: Пинигина Дарья Леонидовна |
ЗАДАНИЕ
Задача №1
Пассажир может уехать на любом из двух маршрутов автобусов. Закон времени ожидания прихода этих автобусов задается графиком плотности распределения вероятности случайной величины ξ:
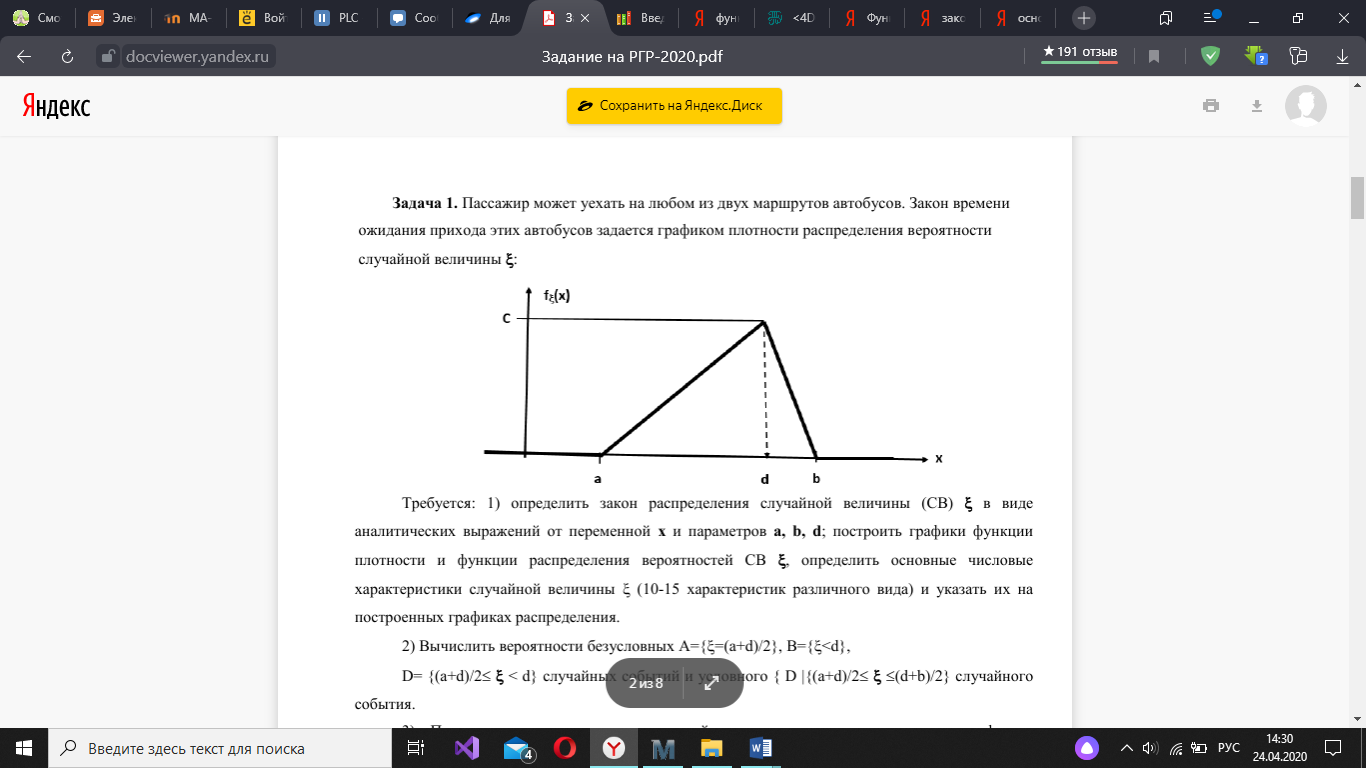
Требуется:
1) определить закон распределения случайной величины (СВ) в виде
аналитических выражений от переменной x и параметров a, b, d; построить графики функции плотности и функции распределения вероятностей СВ , определить основные числовые характеристики случайной величины (10-15 характеристик различного вида) и указать их на построенных графиках распределения.
2) Вычислить вероятности безусловных A={=(a+d)/2}, B={
D= {(a+d)/2 < d} случайных событий и условного { D |{(a+d)/2 (d+b)/2} случайного
события.
3) Проверить правильность вычислений и на основании установленных фактов сформулировать выводы об основных вероятностных свойствах закона распределения вероятностей СВ .
Исходные данные
| Вариант | a | b | d |
| 4 | 0 | 15 | 8 |
Задача №2
Дана двухмерная дискретная случайная величина (ДСВ) (ξ,ƞ) таблицей распределения в виде вероятностной матрицы:
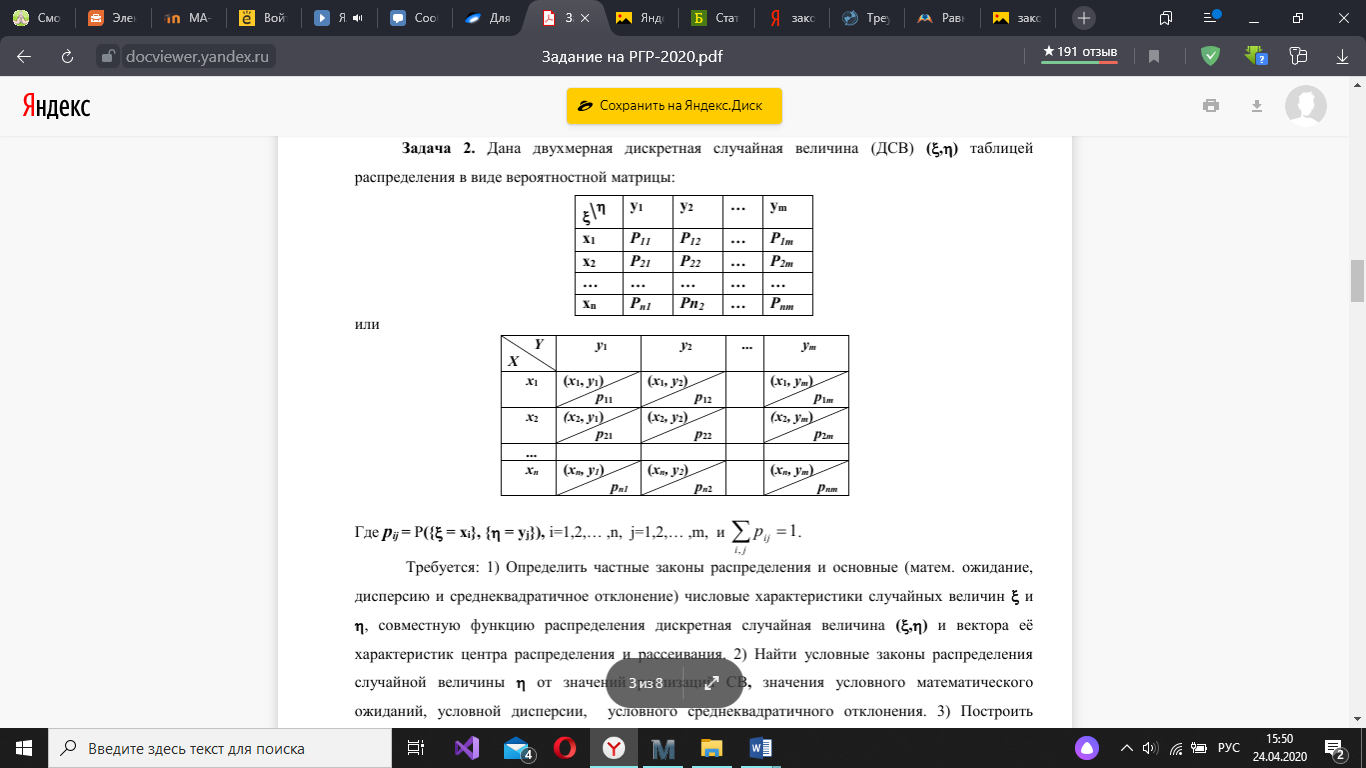
Где pij = P({ = xi}, { = yj}), i=1,2,… ,n, j=1,2,… ,m, и pij 1.
Требуется:
1) Определить частные законы распределения и основные (матем. ожидание,
дисперсию и среднеквадратичное отклонение) числовые характеристики случайных величин и , совместную функцию распределения дискретная случайная величина (,) и вектора её характеристик центра распределения и рассеивания.
2) Найти условные законы распределения случайной величины от значений реализаций СВ, значения условного математического ожиданий, условной дисперсии, условного среднеквадратичного отклонения.
3) Построить графическое изображение совместного закона распределения двухмерной СВ в виде диаграммы рассеивания и наложенными на неё линями условного математического ожиданий и условного среднеквадратичного отклонения СВ | {=xi}.
4) Определить ковариацию, корреляцию, генеральное корреляционное отношение, функцию линейной регрессии и построить её график, совмещенный с графиками условного среднеквадратичного отклонения СВ | {=xi}.
Исходные данные:
| ξƞ | y1 | y2 | y3 | y4 |
| x1 | 0,11 | 0,1 | 0,07 | 0,1 |
| x2 | 0,08 | 0,11 | 0,05 | 0,11 |
| x3 | 0,09 | 0,08 | 0,11 | 0,08 |
P=1, X={ 1, 3, 7}, Y={ 2, 5, 8 ,11}.
| Y X | y1 | y2 | … | ym |
| x1 | (x1, y1) p11 | (x1, y2) p12 | … | (x1, ym) p1m |
| x2 | (x2, y1) P21 | (x2, y2) P22 | … | (x2, ym) P2m |
| … | … | … | … | … |
| xn | (xn, y1) Pn1 | (xn, y2) Pn2 | … | (xn, ym) Pnm |
Задача №3
Дана выборка из непрерывной генеральной совокупности.
1 «Восстановить» распределение генеральной совокупности.
1.1. Подготовить исходные данные (выборку) к виду, удобному для обработки и анализа статистических данных задания в табличной и графической форме.
1.1.1. Описать выборку в виде вариационного, статистического и вероятностных рядов разного типа.
1.1.2. Представить выборку в графической форме (полигоном, гистограммой, круговой диаграммой, кумулятивной кривой и т.д., но не менее 5 видов графиков выборки).
1.1.3. Вычислить не менее 10 описательных статистик: характеристик центра,
рассеивания, коэффициенты формы выборочного распределения выборки и т.д.
1.2. Провести анализ полученных результатов описания выборки: выдвинуть и проверить гипотезу о законе распределения теоретической случайной величины.
1.2.1. Оценить параметры гипотетического распределения.
1.2.2. Построить на одном рисунке графики выборочного и гипотетического закона распределения и оценить степень сходства (различия) между ними.
1.2.3. Проверить по выбранному критерию согласия выдвинутую гипотезу о
распределении наблюдаемой случайной величины на 5% уровне значимости. Что изменится, если уровень значимости 1%?
1.3. Оценить качество оценок параметров закона распределения генеральной совокупности.
1.3.1. Определить погрешность в вычислении параметров (хотя бы одного параметра) распределения за счет группировки исходной выборки.
1.3.2. Построить 95% доверительные интервалы для параметров (параметра)
«теоретического» распределения.
2. Сформулировать и проверить на выбранном (5% уровне) значимости не менее 3 статистических гипотез (по выбору студента) о параметрах и свойствах исследуемой выборки генеральной совокупности.
3. Выберем из заданной в варианте выборки первые три и три последних столбцов и будем считать их независимыми выборками - наблюдениями за С.В. ξ и ƞ соответственно.
3.1. Проверить гипотезу об однородности этих выборок.
3.2. Проверить гипотезу о равенстве средних ξ и ƞ.
3.3. Построить диаграмму рассеяния величин (ξ, ƞ), вычислить выборочный коэффициент корреляции ρ(ξ, ƞ) и аппроксимировать зависимость между ξ и ƞ прямой линией.
Содержание
Введение 6
Задача №1 7
Задача 2 12
Задача №3 18
Заключение 27
Список использованных источников 28
Приложение 29
Введение
Цель работы:
-
Выполняя практические задания закрепить теоретические знания вероятностного и статистического анализа случайных величин, описывающих свойства и закономерности вероятностных экспериментов на основе законов распределений и статистических моделей.
-
Применяя разные способы описания (законов распределения) заданной случайной величины и случайного вектора, установить основные их свойства и дать рекомендации по практическому применению соответствующих функций и характеристик вероятностных экспериментов и статистических моделей.
-
Осуществляя статистическую обработку эмпирических данных, приобрести навыки практического применения основных методов математической статистики для оценки характеристик выборок, определения законов распределения, проверки простых статистических гипотез о свойствах выборки и генеральной совокупности, а также построения и анализа регрессионных моделей вероятностных экспериментов.
-
Реализуя вычислительные эксперименты с разработанными программами анализа свойств одномерных и двухмерных случайных величин, получить те или иные факты, подтверждающие основные положения теории вероятностей и математической статистики, а также общепринятые эмпирические правила вероятностного и статистического моделирования вероятностных экспериментов, распределения вероятностей исследуемой случайной величины.
Выбор инструментальных средств:
MathCad, Microsoft Excel, Microsoft Word.
Задача №1
1.1
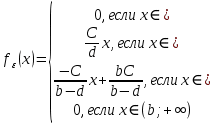
Пропишем условие нормировки:
Найдём С по этому условию:
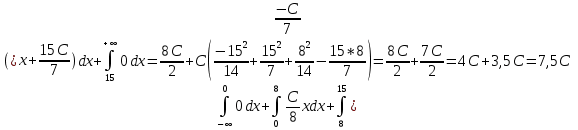
Найдем плотность распределение вероятности
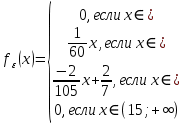
Найдем функцию распределения вероятности по формулам
при
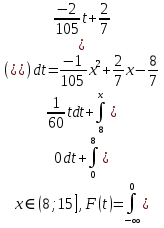
при
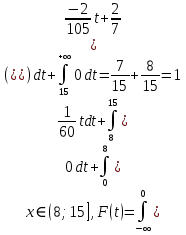
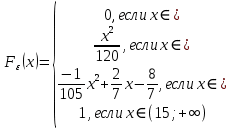
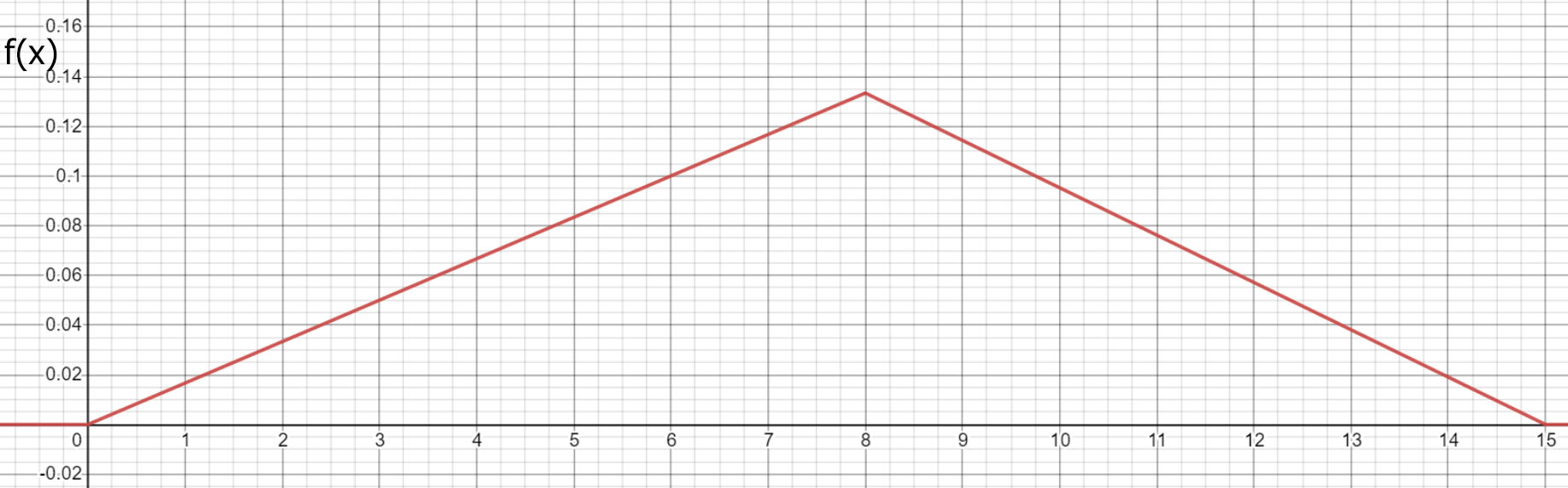
Рис 1.1 График функции плотности распределения [1]
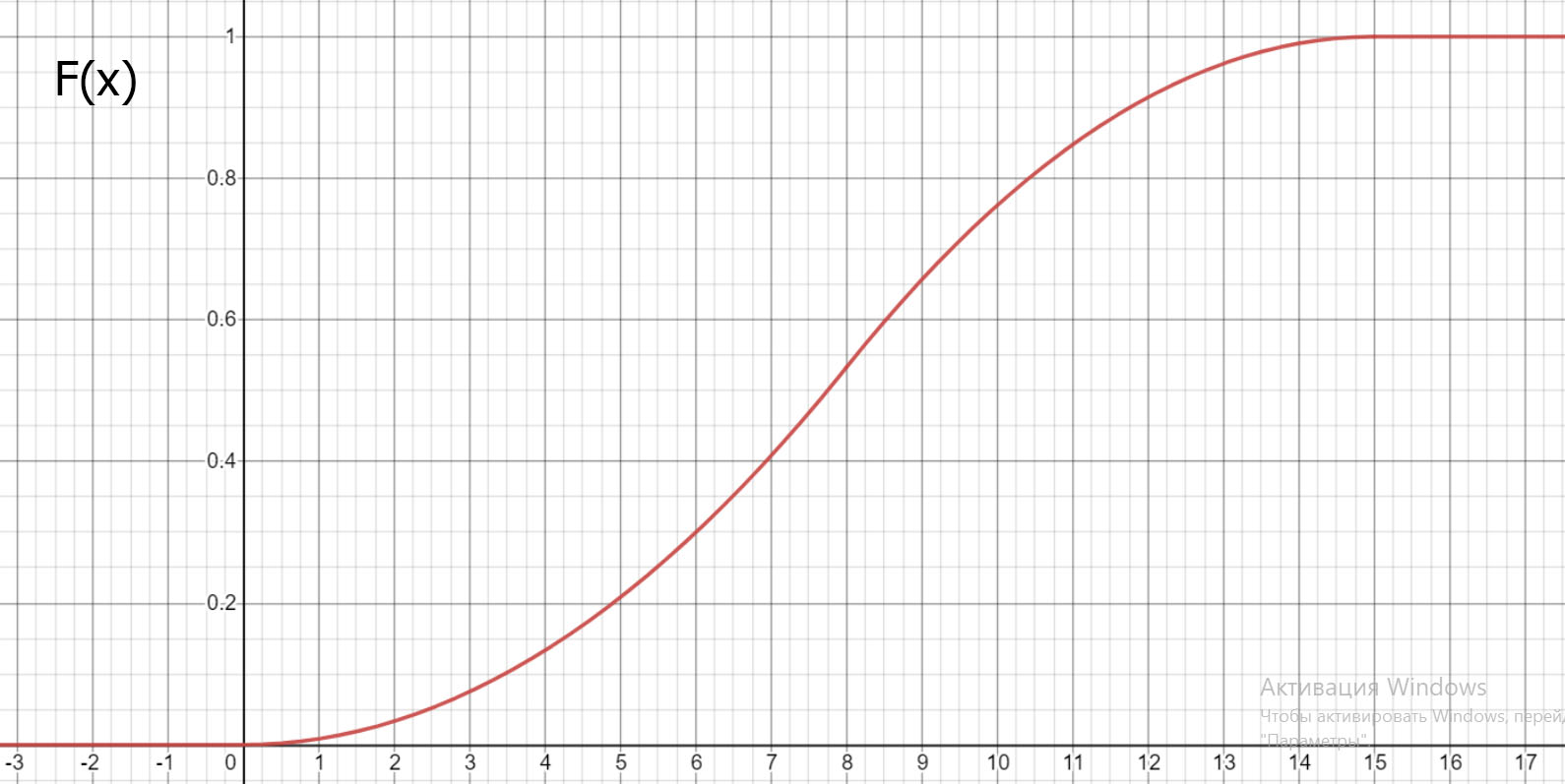
Рис 1.2 График функции распределения вероятностей
Найдём математическое ожидание непрерывной случайной величины
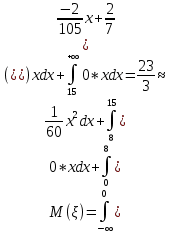 7,66
7,66Найдём дисперсию непрерывной случайной величины
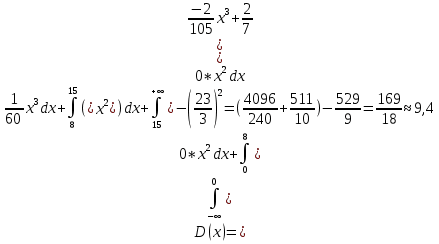
Найдём среднеквадратическое отклонение случайной величины