Файл: Пинигина Дарья Леонидовна задание задача 1 Пассажир может уехать на любом из двух маршрутов автобусов закон.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 76
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
:
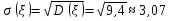
Коэффициент вариации случайной величины :
:
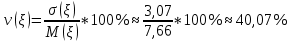
Найдём моду случайной величины :
:
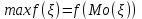
По графику максимуму функции соответствует x = 8, тогда
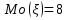
Найдём медиану случайной величины :
:
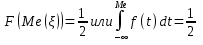
Так как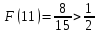 , то
, то 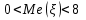 , следовательно
, следовательно
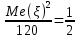
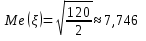
Найдём третий центральный момент случайной величины :
:
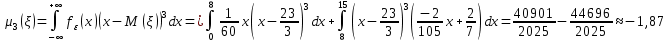
Найдём четвёртый центральный момент случайной величины :
:
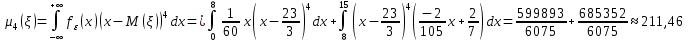
Коэффициент асимметрии случайной величины :
:
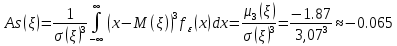
Коэффициент эксцесса случайной величины :
:
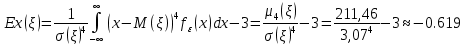
Найдём 25%-ю квантиль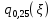 случайной величины
случайной величины  :
:
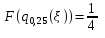
Так как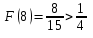 , то
, то 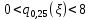 , следовательно
, следовательно
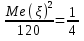
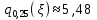
Найдём 75%-ю квантиль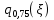 случайной величины
случайной величины  :
:
Так как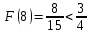 , то
, то 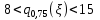 , следовательно
, следовательно
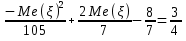
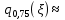 14,11
14,11
1.2
Искомые вероятности:
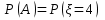 т.к. нету интервала, то определённый интеграл будут с одинаковыми границами значит
т.к. нету интервала, то определённый интеграл будут с одинаковыми границами значит 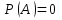
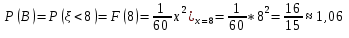
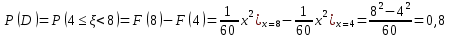
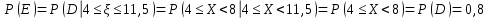
1.3
Среднее время ожидания: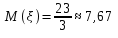
Среднеквадратическое отклонение: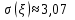
Коэффициент вариации: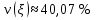
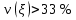 следовательно распределение не является однородным, т.е. среднее значение времени ожидания автобусов
следовательно распределение не является однородным, т.е. среднее значение времени ожидания автобусов 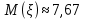
не является характерным значением для рассматриваемой случайной величины
.
Вывод
По графику плотности - треугольный закон распределения (Симпсона)
Исследуемая величина непрерывна (видно по графику плотности). Поскольку коэффициент вариации v( )>33%), распределение не является однородным,
)>33%), распределение не является однородным,  не является характерным значением для рассматриваемой случайной величины
не является характерным значением для рассматриваемой случайной величины  . По графику функции плотности распределения можно заметить, что она непрерывна.
. По графику функции плотности распределения можно заметить, что она непрерывна.
Унимодальное – мода единственна. Асимметрия отрицательна – распределение скошено влево.
Таблица 2.1 Исходные данные
Т.к. сумма вероятностей = 1,09 > 1 то одно из значение изменим на 0
Таблица 2.2 измененные данные
Пусть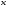 и
и 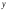 – значения рассматриваемых случайных величин
– значения рассматриваемых случайных величин  и
и  соответственно и
соответственно и 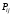 – коэффициенты (
– коэффициенты (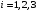 ,
, 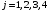 ).
).
1.1
Определение вероятностей значений двухмерной случайной величины (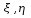 ) [10]
) [10]
Закон распределения случайной величины :
:
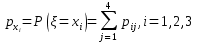 [3]
[3]
или
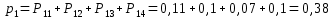
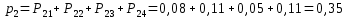
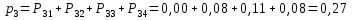
Проверка:
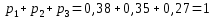
Закон распределения случайной величины :
:
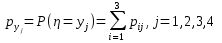
Или
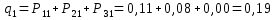
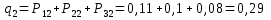
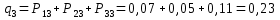
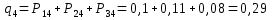
Проверка:
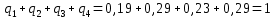
Таблица 2.3 частный закон распределения случайных величин
Коэффициент вариации случайной величины
Найдём моду случайной величины
По графику максимуму функции соответствует x = 8, тогда
Найдём медиану случайной величины
Так как
Найдём третий центральный момент случайной величины
Найдём четвёртый центральный момент случайной величины
Коэффициент асимметрии случайной величины
Коэффициент эксцесса случайной величины
Найдём 25%-ю квантиль
Так как
Найдём 75%-ю квантиль
Так как
1.2
Искомые вероятности:
1.3
Среднее время ожидания:
Среднеквадратическое отклонение:
Коэффициент вариации:
не является характерным значением для рассматриваемой случайной величины
.
Вывод
По графику плотности - треугольный закон распределения (Симпсона)
Исследуемая величина непрерывна (видно по графику плотности). Поскольку коэффициент вариации v(
Унимодальное – мода единственна. Асимметрия отрицательна – распределение скошено влево.
Задача 2
Таблица 2.1 Исходные данные
| \ | y1 | y2 | y3 | y4 |
| x1 | 0,11 | 0,1 | 0,07 | 0,1 |
| x2 | 0,08 | 0,11 | 0,05 | 0,11 |
| x3 | 0. 09 | 0,08 | 0,11 | 0,08 |
| | | | | |
| | | | | |
Т.к. сумма вероятностей = 1,09 > 1 то одно из значение изменим на 0
Таблица 2.2 измененные данные
| | | | | | |
| | | 2 | 5 | 8 | 11 |
| | 1 | 0,11 | 0,1 | 0,07 | 0,1 |
| | 3 | 0,08 | 0,11 | 0,05 | 0,11 |
| | 7 | 0,00 | 0,08 | 0,11 | 0,08 |
Пусть
1.1
Определение вероятностей значений двухмерной случайной величины (
Закон распределения случайной величины
или
Проверка:
Закон распределения случайной величины
Или
Проверка:
Таблица 2.3 частный закон распределения случайных величин