Файл: Пинигина Дарья Леонидовна задание задача 1 Пассажир может уехать на любом из двух маршрутов автобусов закон.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 74
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
– гипотеза принимается для уровня значимости 
Значит средние СВ равны.
3.3.
Выборочный линейный коэффициент корреляции :
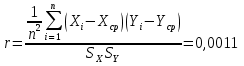
Корреляция крайне мала, связь очень слабая.
Для линейной аппроксимации посчитаем коэффициенты y=ax+b:
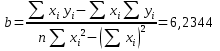
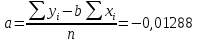
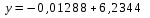
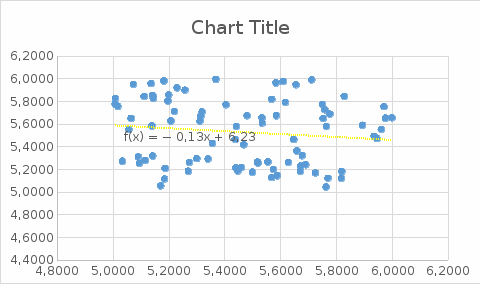
Рис. 3.4 Диаграмма рассеяния величин
Вывод:
Выборочный линейный коэффициент корреляции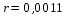
значит связь очень слабая.
Доказав гипотезу, установили, что выборка имеет равномерное распределение
Погрешность Xср = 0,0007 – незначительная.
Коэффициент вариации: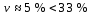
значит выборка однородна
В ходе проделанной работы были закреплены теоретические знания вероятностного и статистического анализа случайных величин.
В задаче №1 определили треугольный закон распределения (Симпсона) случайной величины, вычислили вероятности безусловных случайных событий и условного случайного события.
В задаче №2 была исследована двумерная случайная величина, заданная в виде вероятностной матрицы. Были определены частные законы распределения, и по ним рассчитаны основные числовые характеристики маргинальных случайных величин. Была построена совместная функция распределения и рассчитаны вектора её характеристик центра распределения и рассеивания. Затем были найдены условные законы распределения случайной величины h от значений реализаций СВ ξ, значения условного математического ожиданий, условной дисперсии, условного среднеквадратичного отклонения. Была определена слабая степень связи маргинальных случайных величин и построена линейная регрессия.
В задаче №3 исходная выборка была отформатирована, преобразована в интервальный вариационный ряд и представлена в виде 5 различных графиков. Были вычислены 10 описательных статистик для полученного ряда и исходной выборки. Далее, была выдвинута и доказана при помощи статистики Пирсона гипотеза о равномерном распределении ряда. Построен теоретический график равномерного распределения поверх исходного ряда для сравнения эмпирических функций распределений. Была определена погрешность в вычислении генерального среднего за счёт группировки исходной выборки, а также построен доверительный интервал для него же. Были сформулированы и проверены 3 статистические гипотезы о параметрах и свойствах исследуемой выборки генеральной совокупности. Были отобраны две другие выборки из генеральной совокупности, на них были проверены гипотезы об однородности и равенстве средних, а также построена диаграмма рассеяния величин, вычислен коэффициент корреляции и линейно аппроксимирована зависимость между ними.
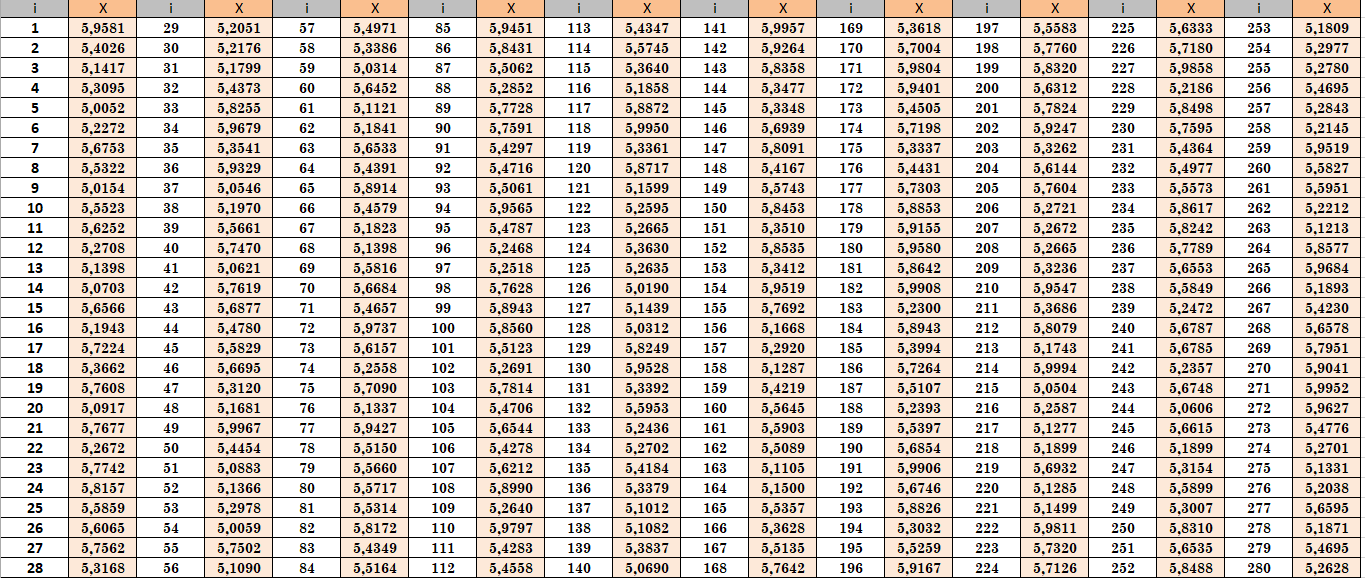
Приложение 1. Выборка
Таблица 1 исходные данные
Таблица 2 Отредактированные данные
Приложение 2. Графики
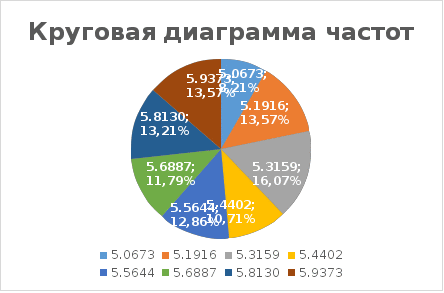
Рис 1 Круговая диаграмма относительных частот
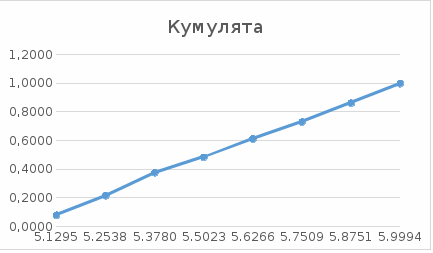
Рис 2 Кумулята
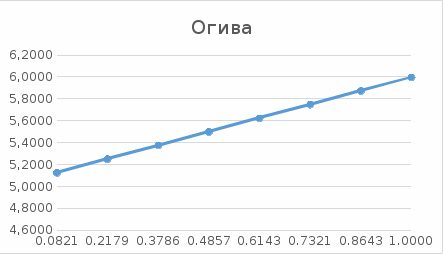
Рис 3 Огива
Приложение 3. Выборка из трёх первых последних столбцов.
Таблица 1. Три первых и последних столбца
Электронные приложения:
Приложение 4. “3 задание.xlsx”
В нём проводятся вычисления и строятся графики для 3 задания.
Приложение 5. “2 задание.xmcd”
В нем проводятся вычисления и строятся графики для 2 задания.
Значит средние СВ равны.
3.3.
Выборочный линейный коэффициент корреляции :
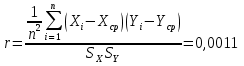
Корреляция крайне мала, связь очень слабая.
Для линейной аппроксимации посчитаем коэффициенты y=ax+b:
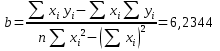
Рис. 3.4 Диаграмма рассеяния величин
Вывод:
Выборочный линейный коэффициент корреляции
значит связь очень слабая.Доказав гипотезу, установили, что выборка имеет равномерное распределение
Погрешность Xср = 0,0007 – незначительная.
Коэффициент вариации:
значит выборка однороднаЗаключение
В ходе проделанной работы были закреплены теоретические знания вероятностного и статистического анализа случайных величин.
В задаче №1 определили треугольный закон распределения (Симпсона) случайной величины, вычислили вероятности безусловных случайных событий и условного случайного события.
В задаче №2 была исследована двумерная случайная величина, заданная в виде вероятностной матрицы. Были определены частные законы распределения, и по ним рассчитаны основные числовые характеристики маргинальных случайных величин. Была построена совместная функция распределения и рассчитаны вектора её характеристик центра распределения и рассеивания. Затем были найдены условные законы распределения случайной величины h от значений реализаций СВ ξ, значения условного математического ожиданий, условной дисперсии, условного среднеквадратичного отклонения. Была определена слабая степень связи маргинальных случайных величин и построена линейная регрессия.
В задаче №3 исходная выборка была отформатирована, преобразована в интервальный вариационный ряд и представлена в виде 5 различных графиков. Были вычислены 10 описательных статистик для полученного ряда и исходной выборки. Далее, была выдвинута и доказана при помощи статистики Пирсона гипотеза о равномерном распределении ряда. Построен теоретический график равномерного распределения поверх исходного ряда для сравнения эмпирических функций распределений. Была определена погрешность в вычислении генерального среднего за счёт группировки исходной выборки, а также построен доверительный интервал для него же. Были сформулированы и проверены 3 статистические гипотезы о параметрах и свойствах исследуемой выборки генеральной совокупности. Были отобраны две другие выборки из генеральной совокупности, на них были проверены гипотезы об однородности и равенстве средних, а также построена диаграмма рассеяния величин, вычислен коэффициент корреляции и линейно аппроксимирована зависимость между ними.
Список использованных источников
-
Зыбарев В.М. Лекция “Непрерывные случайные величины”, конспекты лекций. -
Зыбарев В.М. Лекция “Системы случайных величин”, конспекты лекций. -
Зыбарев В.М. Лекция “Случайные величины (числа). (Основы теории распределений вероятностей)”, конспекты лекций. -
Зыбарев В.М. Лекция “Математическая статистика. Описательная (дескриптивная) статистика”, конспекты лекций. -
Зыбарев В.М. Лекция “Математическая статистика. Статистическое оценивание”, конспекты лекций. -
Зыбарев В.М. Лекция “Интервальное оценивание”, конспекты лекций. -
Зыбарев В.М. Лекция “Проверка непараметрических гипотез”, конспекты лекций. -
Зыбарев В.М. Лекция 13 «Математическая статистика. Проверка статистических гипотез»: конспекты лекции -
Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для втузов. Изд. 9-е, стер. – М: Высш. шк. 2003. – 479 с. -
Калинина В.Н. Математическая статистика: Учеб. для студ. сред. спец. учеб. заведений / В.Н. Калинина, В.Ф. Панкин. – 4-е изд. испр. – М.: Дрофа, 2002. – 336 с. -
Кремер Н.Ш. Теория вероятностей и математическая статистика: учебник для студентов вузов, обучающихся по экономическим специальностям / Н.Ш. Кремер. – 3-е изд., перераб. и доп. – М.: ЮНИТИ-ДАНА, 2010. – 551 с.
Приложение
Приложение 1. Выборка
Таблица 1 исходные данные
| 5,9581 | 5,2051 | 5,4971 | 5,9451 | 5,4347 | 5,9957 | 5,3618 | 5,5583 | 5,6333 | 5,1809 |
| 5,4026 | 5,2176 | 5,3386 | 5,8431 | 5,5745 | 5,9264 | 5,7004 | 5,7760 | 5,7180 | 5,2977 |
| 5,1417 | 5,1799 | 5,0314 | 5,5062 | 5,3640 | 5,8358 | 5,9804 | 5,8320 | 5,9858 | 5,2780 |
| 5,3095 | 5,4373 | 5,6452 | 5,2852 | 5,1858 | 5,3477 | 5,9401 | 5,6312 | 5,2186 | 5,4695 |
| 5,0052 | 5,8255 | 5,1121 | 5,7728 | 5,8872 | 5,3348 | 5,4505 | 5,7824 | 5,8498 | 5,2843 |
| 5,2272 | 5,9679 | 5,1841 | 5,7591 | 5,9950 | 5,6939 | 5,7198 | 5,9247 | 5,7595 | 5,2145 |
| 5,6753 | 5,3541 | 5,6533 | 5,4297 | 5,3361 | 5,8091 | 5,3337 | 5,3262 | 5,4364 | 5,9519 |
| 5,5322 | 5,9329 | 5,4391 | 5,4716 | 5,8717 | 5,4167 | 5,4431 | 5,6144 | 5,4977 | 5,5827 |
| 5,0154 | 5,0546 | 5,8914 | 5,5061 | 5,1599 | 5,5743 | 5,7303 | 5,7604 | 5,5573 | 5,5951 |
| 5,5523 | 5,1970 | 5,4579 | 5,9565 | 5,2595 | 5,8453 | 5,8853 | 5,2721 | 5,8617 | 5,2212 |
| 5,6252 | 5,5661 | 5,1823 | 5,4787 | 5,2665 | 5,3510 | 5,9155 | 5,2672 | 5,8242 | 5,1213 |
| 5,2708 | 5,7470 | 5,1398 | 5,2468 | 5,3630 | 5,8535 | 5,9580 | 5,2665 | 5,7789 | 5,8577 |
| 5,1398 | 5,0621 | 5,5816 | 5,2518 | 5,2635 | 5,3412 | 5,8642 | 5,3236 | 5,6553 | 5,9684 |
| 5,0703 | 5,7619 | 5,6684 | 5,7628 | 5,0190 | 5,9519 | 5,9908 | 5,9547 | 5,5849 | 5,1893 |
| 5,6566 | 5,6877 | 5,4657 | 5,8943 | 5,1439 | 5,7692 | 5,2300 | 5,3686 | 5,2472 | 5,4230 |
| 5,1943 | 5,4780 | 5,9737 | 5,8560 | 5,0312 | 5,1668 | 5,8943 | 5,8079 | 5,6787 | 5,6578 |
| 5,7224 | 5,5829 | 5,6157 | 5,5123 | 5,8249 | 5,2920 | 5,3994 | 5,1743 | 5,6785 | 5,7951 |
| 5,3662 | 5,6695 | 5,2558 | 5,2691 | 5,9528 | 5,1287 | 5,7264 | 5,9994 | 5,2357 | 5,9041 |
| 5,7608 | 5,3120 | 5,7090 | 5,7814 | 5,3392 | 5,4219 | 5,5107 | 5,0504 | 5,6748 | 5,9952 |
| 5,0917 | 5,1681 | 5,1337 | 5,4706 | 5,5953 | 5,5645 | 5,2393 | 5,2587 | 5,0606 | 5,9627 |
| 5,7677 | 5,9967 | 5,9427 | 5,6544 | 5,2436 | 5,5903 | 5,5397 | 5,1277 | 5,6615 | 5,4776 |
| 5,2672 | 5,4454 | 5,5150 | 5,4278 | 5,2702 | 5,5089 | 5,6854 | 5,1899 | 5,1899 | 5,2701 |
| 5,7742 | 5,0883 | 5,5660 | 5,6212 | 5,4184 | 5,1105 | 5,9906 | 5,6932 | 5,3154 | 5,1331 |
| 5,8157 | 5,1366 | 5,5717 | 5,8990 | 5,3379 | 5,1500 | 5,6746 | 5,1285 | 5,5899 | 5,2038 |
| 5,5859 | 5,2978 | 5,5314 | 5,2640 | 5,1012 | 5,5357 | 5,8826 | 5,1499 | 5,3007 | 5,6595 |
| 5,6065 | 5,0059 | 5,8172 | 5,9797 | 5,1082 | 5,3628 | 5,3032 | 5,9811 | 5,8310 | 5,1871 |
| 5,7562 | 5,7502 | 5,4349 | 5,4283 | 5,3837 | 5,5135 | 5,5259 | 5,7320 | 5,6535 | 5,4695 |
| 5,3168 | 5,1090 | 5,5164 | 5,4558 | 5,0690 | 5,7642 | 5,9167 | 5,7126 | 5,8488 | 5,2628 |
Таблица 2 Отредактированные данные
Приложение 2. Графики
Рис 1 Круговая диаграмма относительных частот
Рис 2 Кумулята
Рис 3 Огива
Приложение 3. Выборка из трёх первых последних столбцов.
Таблица 1. Три первых и последних столбца
| первые 3 | последние 3 | ||||
| 5,9581 | 5,2051 | 5,4971 | 5,5583 | 5,6333 | 5,1809 |
| 5,4026 | 5,2176 | 5,3386 | 5,7760 | 5,7180 | 5,2977 |
| 5,1417 | 5,1799 | 5,0314 | 5,8320 | 5,9858 | 5,2780 |
| 5,3095 | 5,4373 | 5,6452 | 5,6312 | 5,2186 | 5,4695 |
| 5,0052 | 5,8255 | 5,1121 | 5,7824 | 5,8498 | 5,2843 |
| 5,2272 | 5,9679 | 5,1841 | 5,9247 | 5,7595 | 5,2145 |
| 5,6753 | 5,3541 | 5,6533 | 5,3262 | 5,4364 | 5,9519 |
| 5,5322 | 5,9329 | 5,4391 | 5,6144 | 5,4977 | 5,5827 |
| 5,0154 | 5,0546 | 5,8914 | 5,7604 | 5,5573 | 5,5951 |
| 5,5523 | 5,1970 | 5,4579 | 5,2721 | 5,8617 | 5,2212 |
| 5,6252 | 5,5661 | 5,1823 | 5,2672 | 5,8242 | 5,1213 |
| 5,2708 | 5,7470 | 5,1398 | 5,2665 | 5,7789 | 5,8577 |
| 5,1398 | 5,0621 | 5,5816 | 5,3236 | 5,6553 | 5,9684 |
| 5,0703 | 5,7619 | 5,6684 | 5,9547 | 5,5849 | 5,1893 |
| 5,6566 | 5,6877 | 5,4657 | 5,3686 | 5,2472 | 5,4230 |
| 5,1943 | 5,4780 | 5,9737 | 5,8079 | 5,6787 | 5,6578 |
| 5,7224 | 5,5829 | 5,6157 | 5,1743 | 5,6785 | 5,7951 |
| 5,3662 | 5,6695 | 5,2558 | 5,9994 | 5,2357 | 5,9041 |
| 5,7608 | 5,3120 | 5,7090 | 5,0504 | 5,6748 | 5,9952 |
| 5,0917 | 5,1681 | 5,1337 | 5,2587 | 5,0606 | 5,9627 |
| 5,7677 | 5,9967 | 5,9427 | 5,1277 | 5,6615 | 5,4776 |
| 5,2672 | 5,4454 | 5,5150 | 5,1899 | 5,1899 | 5,2701 |
| 5,7742 | 5,0883 | 5,5660 | 5,6932 | 5,3154 | 5,1331 |
| 5,8157 | 5,1366 | 5,5717 | 5,1285 | 5,5899 | 5,2038 |
| 5,5859 | 5,2978 | 5,5314 | 5,1499 | 5,3007 | 5,6595 |
| 5,6065 | 5,0059 | 5,8172 | 5,9811 | 5,8310 | 5,1871 |
| 5,7562 | 5,7502 | 5,4349 | 5,7320 | 5,6535 | 5,4695 |
| 5,3168 | 5,1090 | 5,5164 | 5,7126 | 5,8488 | 5,2628 |
Электронные приложения:
Приложение 4. “3 задание.xlsx”
В нём проводятся вычисления и строятся графики для 3 задания.
Приложение 5. “2 задание.xmcd”
В нем проводятся вычисления и строятся графики для 2 задания.