ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 157
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, МПа;
SH – коэффициент запаса прочности;
ZN – коэффициент долговечности;
ZR – коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев;
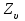 – коэффициент, учитывающий окружную скорость;
– коэффициент, учитывающий окружную скорость;
ZL – коэффициент, учитывающий влияние вязкости масла;
ZX – коэффициент, учитывающий размер зубчатого колеса.
В проектировочном расчете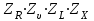 = 0,9.
= 0,9.
В качестве допускаемого контактного напряжения для косозубой передачи при проектировочном расчете принимают условное допускаемое контактное напряжение, определяемое по формуле
для косозубой передачи при проектировочном расчете принимают условное допускаемое контактное напряжение, определяемое по формуле
 =
= 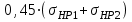 . (2.6)
. (2.6)
При этом должно выполняться условие < 1,23
< 1,23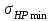 , где
, где 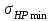 – меньшее из значений
– меньшее из значений 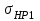 и
и 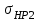 . В противном случае принимают
. В противном случае принимают  =
=
=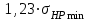 .
.
Предел контактной выносливости , соответствующий базовому числу циклов напряжений, принимают по табл. 2.5.
, соответствующий базовому числу циклов напряжений, принимают по табл. 2.5.
Таблица 2.5
Предел контактной выносливости при базовом числе циклов
При отсутствии необходимых фактических данных можно применить следующие минимальные коэффициенты запаса прочности SH:
– для зубчатых колес, выполненных из материала однородной структуры, принимаем SHmin = 1,1;
– для колес с поверхностным упрочнением зубьев SHmin = 1,2;
– для передач, выход из строя которых связан с тяжелыми последствиями, значения минимальных коэффициентов запасов прочности следует увеличить до SHmin = 1,25 и SHmin = 1,35 соответственно.
Коэффициент долговечности ZN принимают в зависимости от отношения суммарного и базового чисел циклов перемены напряжений в зубьях NK и NHlim по следующим формулам:
ZN =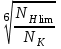 при
при 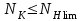 , (2.7)
, (2.7)
но не более 2,6 для однородной структуры материала и 1,8 для поверхностного упрочнения;
ZN =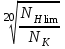 при NK >
при NK > 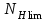 , (2.8)
, (2.8)
но не менее 0,75,
где NHlim – базовое число циклов перемены напряжений;
NК – суммарное число циклов перемены напряжений.
Суммарное число циклов перемены напряжений NК при постоянной нагрузке определяется следующим образом (и для шестерни, и для колеса):
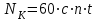 , (2.9)
, (2.9)
где с – число зубчатых колес, сцепляющихся с рассчитываемым зубчатым колесом (в данном задании с = 1);
n – частота вращения рассчитываемого зубчатого колеса, об/мин;
t – срок службы передачи, в часах.
Если не задано конкретное число часов работы передачи, а задан срок работы передачи в годах, то t определятся по формуле
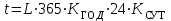 , (2.10)
, (2.10)
где L – срок службы в годах;
КГОД, КСУТ– коэффициенты использования передачи в течение года и суток соответственно.
Базовое число циклов перемены напряжений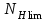 определяется по графику, представленному на рис. 2.6.
определяется по графику, представленному на рис. 2.6.
Используя все найденные параметры, определяют межосевое расстояние. Полученное межосевое расстояние при необходимости округляется до стандартного значения:
Значения первого ряда следует предпочитать значениям второго.
1. Ориентировочно значение модуля при проектировочном расчете зубчатых передач можно принять, мм:
– при твердости Н350НВ m= (0,01...0,02)aw; (2.11)
– при твердости H45HRCэ т = (0,016...0,0315)aw. (2.12)
По ГОСТ 9563–80 принимают стандартный нормальный модуль:
Значения первого ряда следует предпочитать значениям второго.
2. Определяется суммарное число зубьев и число зубьев шестерни и колеса:
– предварительно принимают угол наклона зубьев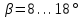 и определяют суммарное zC число зубьев шестерни z1 и колеса z2:
и определяют суммарное zC число зубьев шестерни z1 и колеса z2:
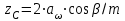 ; (2.13)
; (2.13)
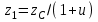 ; (2.14)
; (2.14)
– полученные значения чисел зубьев округляем до целого числа:
z2 = zС –z1. (2.15)
3. Определяются действительное передаточное число и его погрешность:
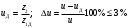 . (2.16)
. (2.16)
Погрешность передаточного числа не должна превышать 3 %.
4. Уточняем значение угла β:
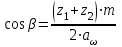 , (2.17)
, (2.17)
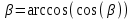 . (2.18)
. (2.18)
Значение угла наклона зубьев необходимо вычислять с точностью до секунд.
5. Далее определяются основные размеры шестерни и колеса.
Делительные диаметры шестерни и колеса:
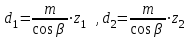 . (2.19)
. (2.19)
6. Проверку полученных диаметров можно провести с помощью формулы
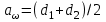 . (2.20)
. (2.20)
Проверкой должно быть установлено, что межосевое расстояние сходится со значением, принятым ранее.
7. Диаметры вершин зубьев определяются по формулам:
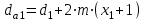 ,
, 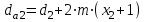 . (2.21)
. (2.21)
Диаметры впадин:
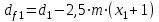 ,
, 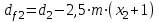 , (2.22)
, (2.22)
где
x – коэффициент смещения, мм.
8. Ширина колеса определяется по формуле, мм:
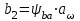 . (2.23)
. (2.23)
Полученное значение ширины колеса округляем до нормального линейного размера.
9. Ширина шестерни определяется по формуле, мм:
b1 = b2 + (5...10). (2.24)
Полученное значение ширины округляем до нормального линейного размера.
10. Определим окружную скорость зубчатых колес по формуле, м/с:
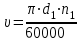 . (2.25)
. (2.25)
11. По окружной скорости колес с учетом рекомендации табл. 2.6 назначают степень точности зубчатых колес.
Таблица 2.6
Нормы точности зубчатых колес
2.3. Проверочный расчет на контактную выносливость активных поверхностей зубьев
Контактная выносливость устанавливается сопоставлением, действующим в полюсе зацепления расчетного и допускаемого контактного напряжений:
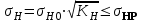 , (2.26)
, (2.26)
где KH – коэффициент нагрузки;
SH – коэффициент запаса прочности;
ZN – коэффициент долговечности;
ZR – коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев;
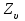 – коэффициент, учитывающий окружную скорость;
– коэффициент, учитывающий окружную скорость;ZL – коэффициент, учитывающий влияние вязкости масла;
ZX – коэффициент, учитывающий размер зубчатого колеса.
В проектировочном расчете
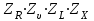 = 0,9.
= 0,9.В качестве допускаемого контактного напряжения
 для косозубой передачи при проектировочном расчете принимают условное допускаемое контактное напряжение, определяемое по формуле
для косозубой передачи при проектировочном расчете принимают условное допускаемое контактное напряжение, определяемое по формуле =
= 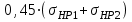 . (2.6)
. (2.6)При этом должно выполняться условие
 < 1,23
< 1,23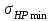 , где
, где 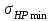 – меньшее из значений
– меньшее из значений 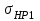 и
и 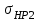 . В противном случае принимают
. В противном случае принимают  =
= =
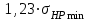 .
.Предел контактной выносливости
 , соответствующий базовому числу циклов напряжений, принимают по табл. 2.5.
, соответствующий базовому числу циклов напряжений, принимают по табл. 2.5.Таблица 2.5
Предел контактной выносливости при базовом числе циклов

| Способ термической и химико-термической обработки зубьев | Средняя твердость поверхности зубьев | Сталь | Формула для расчета значений  |
| Отжиг, нормализация или улучшение | Менее НВ 350 | Углеродистая и легированная |  = = 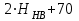 |
| Объемная и поверхностная закалка | HRC 38…50 |  = =  | |
| Цементация и нитроцементация | Более HRC 56 | Легированная |  = = 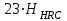 |
| Азотирование | HV 550…750 |  = 1050 = 1050 |
При отсутствии необходимых фактических данных можно применить следующие минимальные коэффициенты запаса прочности SH:
– для зубчатых колес, выполненных из материала однородной структуры, принимаем SHmin = 1,1;
– для колес с поверхностным упрочнением зубьев SHmin = 1,2;
– для передач, выход из строя которых связан с тяжелыми последствиями, значения минимальных коэффициентов запасов прочности следует увеличить до SHmin = 1,25 и SHmin = 1,35 соответственно.
Коэффициент долговечности ZN принимают в зависимости от отношения суммарного и базового чисел циклов перемены напряжений в зубьях NK и NHlim по следующим формулам:
ZN =
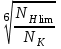 при
при 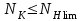 , (2.7)
, (2.7)но не более 2,6 для однородной структуры материала и 1,8 для поверхностного упрочнения;
ZN =
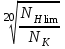 при NK >
при NK > 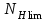 , (2.8)
, (2.8)но не менее 0,75,
где NHlim – базовое число циклов перемены напряжений;
NК – суммарное число циклов перемены напряжений.
Суммарное число циклов перемены напряжений NК при постоянной нагрузке определяется следующим образом (и для шестерни, и для колеса):
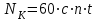 , (2.9)
, (2.9)где с – число зубчатых колес, сцепляющихся с рассчитываемым зубчатым колесом (в данном задании с = 1);
n – частота вращения рассчитываемого зубчатого колеса, об/мин;
t – срок службы передачи, в часах.
Если не задано конкретное число часов работы передачи, а задан срок работы передачи в годах, то t определятся по формуле
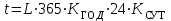 , (2.10)
, (2.10)где L – срок службы в годах;
КГОД, КСУТ– коэффициенты использования передачи в течение года и суток соответственно.
Базовое число циклов перемены напряжений
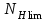 определяется по графику, представленному на рис. 2.6.
определяется по графику, представленному на рис. 2.6.
 , млн циклов , млн циклов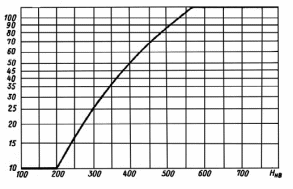 |
| Рис. 2.6. График для определения базового числа циклов перемены напряжений  |
Используя все найденные параметры, определяют межосевое расстояние. Полученное межосевое расстояние при необходимости округляется до стандартного значения:
-
РЯД 1 – 40, 50, 63, 80, 100, 125, 160, 200, 250, 315, 400; -
РЯД 2 – 71, 90, 112, 140, 180, 225, 280, 355, 450.
Значения первого ряда следует предпочитать значениям второго.
2.2. Проектирование передачи
1. Ориентировочно значение модуля при проектировочном расчете зубчатых передач можно принять, мм:
– при твердости Н350НВ m= (0,01...0,02)aw; (2.11)
– при твердости H45HRCэ т = (0,016...0,0315)aw. (2.12)
По ГОСТ 9563–80 принимают стандартный нормальный модуль:
-
РЯД 1 – 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; -
РЯД 2 – 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14.
Значения первого ряда следует предпочитать значениям второго.
2. Определяется суммарное число зубьев и число зубьев шестерни и колеса:
– предварительно принимают угол наклона зубьев
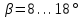 и определяют суммарное zC число зубьев шестерни z1 и колеса z2:
и определяют суммарное zC число зубьев шестерни z1 и колеса z2: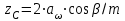 ; (2.13)
; (2.13)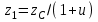 ; (2.14)
; (2.14)– полученные значения чисел зубьев округляем до целого числа:
z2 = zС –z1. (2.15)
3. Определяются действительное передаточное число и его погрешность:
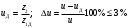 . (2.16)
. (2.16)Погрешность передаточного числа не должна превышать 3 %.
4. Уточняем значение угла β:
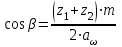 , (2.17)
, (2.17)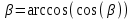 . (2.18)
. (2.18)Значение угла наклона зубьев необходимо вычислять с точностью до секунд.
5. Далее определяются основные размеры шестерни и колеса.
Делительные диаметры шестерни и колеса:
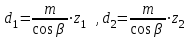 . (2.19)
. (2.19)6. Проверку полученных диаметров можно провести с помощью формулы
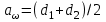 . (2.20)
. (2.20)Проверкой должно быть установлено, что межосевое расстояние сходится со значением, принятым ранее.
7. Диаметры вершин зубьев определяются по формулам:
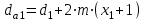 ,
, 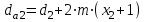 . (2.21)
. (2.21)Диаметры впадин:
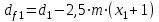 ,
, 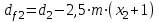 , (2.22)
, (2.22)где
x – коэффициент смещения, мм.
8. Ширина колеса определяется по формуле, мм:
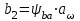 . (2.23)
. (2.23)Полученное значение ширины колеса округляем до нормального линейного размера.
9. Ширина шестерни определяется по формуле, мм:
b1 = b2 + (5...10). (2.24)
Полученное значение ширины округляем до нормального линейного размера.
10. Определим окружную скорость зубчатых колес по формуле, м/с:
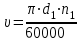 . (2.25)
. (2.25)11. По окружной скорости колес с учетом рекомендации табл. 2.6 назначают степень точности зубчатых колес.
Таблица 2.6
Нормы точности зубчатых колес
| Степень точности по ГОСТ 1643–81 | Окружная скорость, м/с | |
| Прямые зубья | Непрямые зубья | |
| 5 и выше | 15 | 30 |
| 6 | 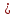 15 15 | 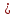 30 30 |
| 7 | 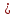 10 10 | 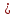 15 15 |
| 8 | 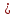 6 6 | 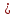 10 10 |
| 9 | 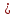 2 2 | 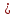 4 4 |
2.3. Проверочный расчет на контактную выносливость активных поверхностей зубьев
А. Определение расчетного контактного напряжения
Контактная выносливость устанавливается сопоставлением, действующим в полюсе зацепления расчетного и допускаемого контактного напряжений:
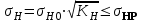 , (2.26)
, (2.26)где KH – коэффициент нагрузки;