Файл: Спецификация суммативного оценивания за четверть по предмету Геометрия.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 220
Скачиваний: 1
СОДЕРЖАНИЕ
Уровни мыслительных навыков по предмету «Геометрия»
Распределение проверяемых целей по уровням мыслительных навыков в разрезе четвертей
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 1 ЧЕТВЕРТЬ
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 1 четверть
Образец заданий и схема выставления баллов
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 2 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 2 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 2 четверть
Образец заданий и схема выставления баллов
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 3 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 3 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 3 четверть
Образец заданий и схема выставления баллов
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 4 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 4 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 4 четверть
| № | Ответ | Балл | Дополнительная информация |
| 1 a | 27,84 (м) | 1 | |
| 1 b | 1948,8 ( м2 ) | 1 | |
| 2 | Рассмотрена равнобедренная трапеция с основаниями 8 и 10 и углом при основании 45 | 1 | |
| Высота боковой грани равна 2 | 1 | | |
| S 1 2 32 40 36 2 бок 2 | 1 | | |
| 3 | 2 1 5 0 13 5 | 1 | |
| cos 5 5 1 4 25 1 1 0 9 10 3 2 3 | 1 | | |
| arccos 1 2 3 | 1 | | |
| 4 a) | 6 3 2 4 p1 p 2 | 1 | |
| p 1 2 | 1 | | |
| 4 b) | 64 p1 3 p 2 2 1 0 | 1 | |
| p 2 3 | 1 | | |
| 5 | 0; 2; 2 - направляющий вектор прямой, 2; 4; 2 - вектор-нормаль к плоскости | 1 | Видно или подразумевается |
| cos 0 8 4 3 4 4 4 16 4 2 | 1 | | |
| 150 - тупой угол между нормалью и прямой | 1 | | |
| 60 - острый угол между прямой и плоскостью | 1 | | |
| 6 | MN CC1 F | 1 | |
| | 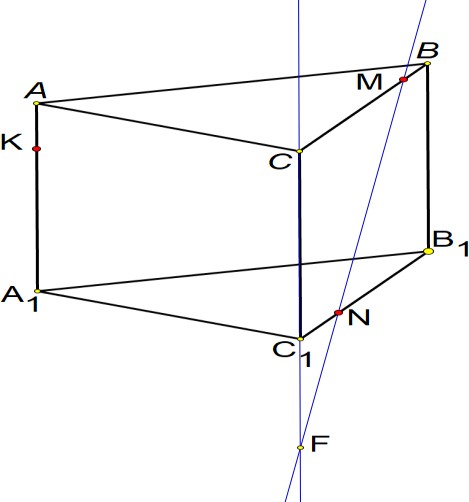 | | |
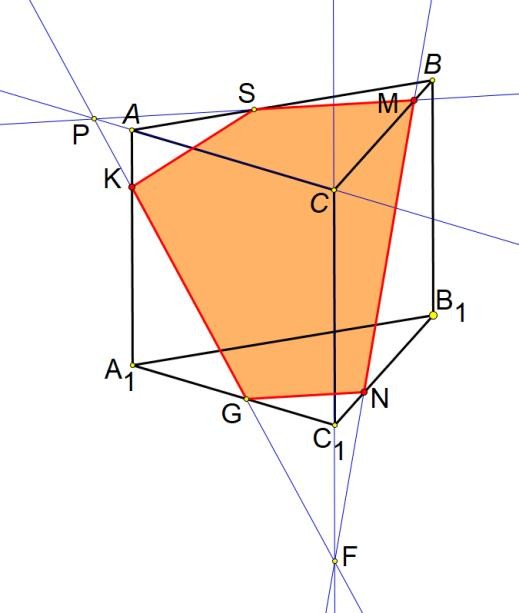
| KF A1C1 G, KF AC P | 1 | | |
| PM AB S | 1 | | |
| KSMNG— искомое сечение | 1 | |
| |  | | |
| Итого: | 20 | | |
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 3 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 3 четверть
Продолжительность – 40 минут
Количество баллов – 20
Типы заданий:
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 5 заданий, включающих вопросы с кратким и развернутым ответами.
В вопросах, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.
В вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов.
19
Характеристика заданий суммативного оценивания за 3 четверть
| Раздел | Проверяемая цель | Уровень мыслительных навыков | Кол. заданий* | № задания* | Тип задани я* | Время на выполнение, мин* | Балл* | Балл за раздел |
| Тела вращения и их элементы | 11.3.4 - выводить формулы площади боковой и полной поверхности цилиндра и применять их при решении задач | Применение | 1 | 3 | РО | 8 мин | 4 | 20 |
| 11.3.5 - решать задачи на нахождение элементов тел вращения (цилиндра, конуса, усеченного конуса, шара) | Применение | 1 | 5 | РО | 10 мин | 5 | ||
| 11.3.6 - выводить формулы площади боковой и полной поверхности конуса и применять их при решении задач | Применение | 1 | 2 | КО/РО | 8 мин | 4 | ||
| 11.3.7 - выводить формулы площади боковой и полной поверхности усеченного конуса и применять их при решении задач | Применение | 1 | 4 | РО | 8 мин | 4 | ||
| 11.1.10 - знать определение сферы, шара; уметь изображать их на плоскости | Знание и понимание | 1 | 1 a,b | КО/РО | 2 мин | 1 | ||
| 11.3.10 - решать задачи, связанные с сечениями шара и сферы плоскостью | Применение | 4 мин | 2 | |||||
| ИТОГО: | | | 5 | | | 40 мин | 20 | 20 |
| Примечание:*-разделы,вкоторыеможновноситьизменения | ||||||||
20
Образец заданий и схема выставления баллов
Задания суммативного оценивания за 3 четверть по предмету «Математика»
-
Вершины прямоугольного треугольника лежат на сфере радиусом 6 см.-
Выполните рисунок по условию задачи.
-
-
Найдите расстояние от центра сферы до плоскости треугольника, если его гипотенуза равна 4 см.
[1]
[2]
2.
-
 Круговой сектор радиуса 12 ограничен дугой с градусной мерой 135 . Вычислите площадь данногосектора.
Круговой сектор радиуса 12 ограничен дугой с градусной мерой 135 . Вычислите площадь данногосектора.
[2]
-
Сектор свернули в конус. Используя результат предыдущего пункта, найдите радиус конуса.
[2]
-
Мячик для настольного тенниса имеет радиус 20 мм. Мячи плотно укладывают в пластиковый контейнер по 6 штук, как показано на рисунке. (Мячи касаются дна, стенок и крышки контейнера)

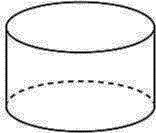 Крышка контейнера также имеет форму цилиндра радиусом 21 мм, высотой 15 мм. Рассчитайте площадь пластика, необходимого для изготовления одного контейнера.
Крышка контейнера также имеет форму цилиндра радиусом 21 мм, высотой 15 мм. Рассчитайте площадь пластика, необходимого для изготовления одного контейнера.[4]
-
 Диагональ осевого сечения усеченного конуса является биссектрисой острого угла при основании этого сечения. Образующая равна 8 и образует угол 60 с плоскостью основания. Выполнив рисунок, найдите площадь полной поверхности усеченного конуса.
Диагональ осевого сечения усеченного конуса является биссектрисой острого угла при основании этого сечения. Образующая равна 8 и образует угол 60 с плоскостью основания. Выполнив рисунок, найдите площадь полной поверхности усеченного конуса.
[4]
21