Файл: Спецификация суммативного оценивания за четверть по предмету Геометрия.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 12.01.2024

Просмотров: 213

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

СОДЕРЖАНИЕ

Уровни мыслительных навыков по предмету «Геометрия»

Распределение проверяемых целей по уровням мыслительных навыков в разрезе четвертей

СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 1 ЧЕТВЕРТЬ

Количество баллов – 20

Структура суммативного оценивания

Характеристика заданий суммативного оценивания за 1 четверть

Образец заданий и схема выставления баллов

СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 2 ЧЕТВЕРТЬ

Обзор суммативного оценивания за 2 четверть

Количество баллов – 20

Структура суммативного оценивания

Характеристика заданий суммативного оценивания за 2 четверть

Образец заданий и схема выставления баллов

СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 3 ЧЕТВЕРТЬ

Обзор суммативного оценивания за 3 четверть

Количество баллов – 20

Структура суммативного оценивания

Характеристика заданий суммативного оценивания за 3 четверть

Образец заданий и схема выставления баллов

СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 4 ЧЕТВЕРТЬ

Обзор суммативного оценивания за 4 четверть

Количество баллов – 20

Структура суммативного оценивания

Характеристика заданий суммативного оценивания за 4 четверть

Образец заданий и схема выставления баллов



5 a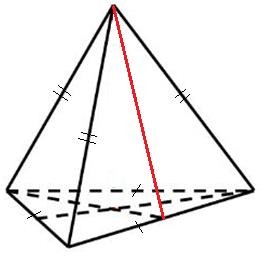


1







1




5 b
Высота основания 3 3
1



Использовано 2 3 ( 2 высоты основания)

3
1



8
1



Итого:
20





СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 2 ЧЕТВЕРТЬ

Обзор суммативного оценивания за 2 четверть



Продолжительность – 40 минут

Количество баллов – 20


Типы заданий:

КО – задания, требующие краткого ответа;

РО – задания, требующие развернутого ответа.

Структура суммативного оценивания



Данный вариант состоит из 6 заданий, включающих вопросы с кратким и развернутым ответами.

В вопросах, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.

В вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов.

12

Характеристика заданий суммативного оценивания за 2 четверть





Раздел

Проверяемая цель
Уровень мыслительных навыков
Кол.

заданий*
№

задания*
Тип

задания*
Время на выполнение, мин*

Балл*
Балл за

раздел



Многогранни ки
11.3.2 выводить формулы площади боковой и полной поверхности пирамиды (усеченной пирамиды) и применять их при решении задач

Применение

2
1
КО/РО
4 мин
2


9

2
РО
6 мин
3

11.2.1 уметь строить сечения многогранника плоскостью
Применение
1
6
РО
8 мин
4



Применение уравнений прямой и плоскости в пространстве
11.4.2 находить угол между прямыми (по заданным уравнениям

прямых)

Применение

1

3

КО/РО

6 мин

3

11

11.4.3 применять условие параллельности и

перпендикулярности прямых в пространстве при решении задач

Применение

1

4

РО

8 мин

4

11.4.5 находить угол между прямой и плоскостью
Применение
1
5
РО
8 мин
4

ИТОГО:






6






40 мин
20
20

Примечание:*-разделы,вкоторыеможновноситьизменения


13

Образец заданий и схема выставления баллов


Задания суммативного оценивания за 2 четверть по предмету «Математика»


  1. Большая пирамида Лувра в Париже имеет форму правильной четырехугольной пирамиды высотой 21,65 м и длиной стороны основания 35 м.



    1. Найдите апофему пирамиды.

Ответокруглитедосотых.


    1. Найдите площадь стеклянной поверхности пирамиды.



[1]
[1]




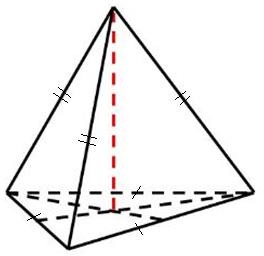
  1. В правильной усеченной четырехугольной пирамиде стороны оснований равны 8 и 10, а боковые грани наклонены к плоскости основания под углом 45 .

Найдите площадь боковой поверхности пирамиды.

[3]


x 3 2,



  1. Найдите угол между прямыми, заданными уравнениями y 5,



z 3  

x 5 ,



и y 5, .



z 2  3

[3]



x 2 4 p1 ,

  1. Прямая l1 задана уравнением y 5 p 2,



z 1 

x 1 6,
где p— некоторое число.

Прямая lзадана уравнением y 4 3, .

2



z 3  2

Найдите значение р, при котором:

    1. прямые l1 и l2 параллельны;



[2]


    1. прямые l1 и l2 перпендикулярны.


[2]

x 1,



  1. Найдите острый угол между прямой y 3  2,



z 4  2
и плоскостью 2x 4y 2z 7 0 .

[4]




  1. Постройте сечение многогранника плоскостью, проходящей через точки K, Mи N. Кратко опишите построение.




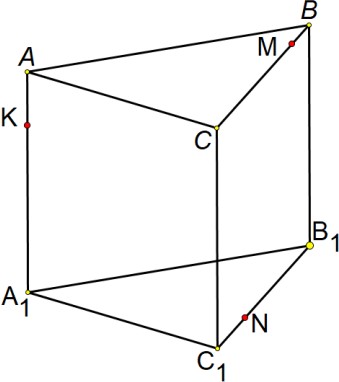
[4]
Схема выставления

Смотрите также файлы