Файл: Спецификация суммативного оценивания за четверть по предмету Геометрия.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 222
Скачиваний: 1
СОДЕРЖАНИЕ
Уровни мыслительных навыков по предмету «Геометрия»
Распределение проверяемых целей по уровням мыслительных навыков в разрезе четвертей
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 1 ЧЕТВЕРТЬ
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 1 четверть
Образец заданий и схема выставления баллов
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 2 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 2 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 2 четверть
Образец заданий и схема выставления баллов
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 3 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 3 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 3 четверть
Образец заданий и схема выставления баллов
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 4 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 4 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 4 четверть
После окончания времени, отведенного на суммативное оценивание, обучающиеся должны вовремя прекратить работу и положить свои ручки/ карандаши на парту.
-
Модерация и выставление баллов
Учителя проводят стандартизацию схемы выставления баллов, которую используют в проверке суммативного оценивания за четверть. В процессе модерации необходимо проверять образцы работ с выставленными баллами для того, чтобы не допускать отклонения от единой схемы выставления баллов.
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 1 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 1 четверть
Продолжительность – 40 минут
Количество баллов – 20
Типы заданий:
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 9 заданий, включающих вопросы с кратким и развернутым ответами.
В вопросах, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.
В вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов.
6
Характеристика заданий суммативного оценивания за 1 четверть
| Раздел | Проверяемая цель | Уровень мыслительных навыков | Кол. заданий* | № задания* | Тип задания* | Время на выполнение, мин* | Балл* | Балл за раздел |
| Многогранни ки | 11.1.2 знать определение многогранника и его элементов | Знание и понимание | 1 | 1 | КО | 2 мин | 1 | 20 |
| 11.3.3 решать задачи на нахождение элементов многогранников | Применение | 4 | 2 | РО | 6 мин | 3 | ||
| 3 c | КО | 4 мин | 2 | |||||
| 4 c | КО | 4 мин | 2 | |||||
| 5 b | РО | 6 мин | 3 | |||||
| 11.3.1 выводить формулы площади боковой и полной поверхности призмы и применять их при решении задач | Применение | 1 | 4 a,b | РО | 6 мин | 3 | ||
| РО | 4 мин | 2 | ||||||
| 11.1.4 знать определение пирамиды, ее элементов, виды пирамид; уметь изображать их на плоскости | Знание и понимание | 2 | 3 a | КО | 2 мин | 1 | ||
| 5 a | КО | 4 мин | 2 | |||||
| 11.2.4 определять расположение проекции вершины пирамиды на плоскость основания | Применение | 1 | 3 b | КО | 2 мин | 1 | ||
| ИТОГО: | | | 9 | | | 40 мин | 20 | 20 |
| Примечание:*-разделы,вкоторыеможновноситьизменения | ||||||||
7
Образец заданий и схема выставления баллов
Задания суммативного оценивания за 1 четверть по предмету «Математика»
-
Известно, что n-угольная пирамида имеет 48 ребер. Чему равно n?
-
 В основании прямой призмы лежит ромб с острым углом 60 и стороной 8 см. Найдите диагонали призмы, если ее боковое ребро равно 4 см.
В основании прямой призмы лежит ромб с острым углом 60 и стороной 8 см. Найдите диагонали призмы, если ее боковое ребро равно 4 см.
[1]
[3]
-
 Строители собрали конструкцию в форме пирамиды, две равные боковые грани которой перпендикулярны основанию, а третья грань образует с ней угол в 60 .
Строители собрали конструкцию в форме пирамиды, две равные боковые грани которой перпендикулярны основанию, а третья грань образует с ней угол в 60 .
Основание конструкции расположено горизонтально на поверхности земли.
-
Постройте изображение конструкции.
[1]
-
Из вершины конструкции, находящейся над землей, опустили отвес (груз на веревочке) до основания. Укажите на изображении точку, в которую попадёт отвес.
[1]
-
Две равные стороны основания равны 10 м, а третья сторона 12 м. Найдите высоту конструкции.
[2]
-
Палатка туристов имеет форму треугольной призмы, как показано на рисунке.
Известно, что
AB AC 1, 4 м,
BC 1, 6 м,
BB1 2, 5 м, высота палатки 1,2 м.
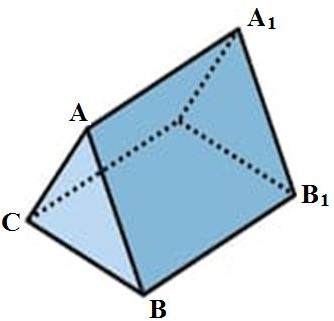
-
Найдите площадь материала, необходимого для изготовления всей палатки, включая днище.
[3]
8
-
Материал для изготовления палатки продается в рулонах шириной 3,7 м.
Ни одна из граней палатки не должна быть сшита из кусков, швы только по ребрам палатки. Нарисуйте схематично, как расположить на ткани выкройку палатки, чтобы расход ткани был наименьшим. (Не учитывать припуски на швы)
Сколько метров ткани потребуется?
-
Каркас палатки изготовлен из алюминиевых трубок.
Сколько метров трубок потребовалось для палатки? (Не учитывать стыки)
5.
[2]
[2]
-
Нарисуйте изображение правильной треугольной пирамиды. Изобразите апофему и высоту пирамиды.
[2]
-
Сторона основания правильной треугольной пирамиды равна 6 см, а боковое ребро –
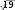 2 см.
2 см.Найдите высоту пирамиды.
[3]



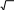 Схема выставления баллов
Схема выставления баллов | № | Ответ | Балл | Дополнительная информация |
| 1 | 24 | 1 | |
| 2 | Длина меньшей диагонали призмы 42 82 4 5 | 1 | |
| 82 42 4 3 Длина большей диагонали ромба 8 3 | 1 | Принимается альтернаттинвое решение | |
| Длина большей диагонали призмы ( 192 )2 42 4 13 или эквивалент | 1 | | |
| 3 a |  | 1 | |
| 3 b | Указана точка В | 1 | |
| 3 c | Высота основания 8 (м) | 1 | |
| 8 3 | 1 | | |
| 4 a | 1, 4 2,5 или1, 6 2,5 | 1 | |
| 1 1, 6 1, 2 2 | 1 | | |
| 12,92 м2 | 1 | | |
| 4 b | 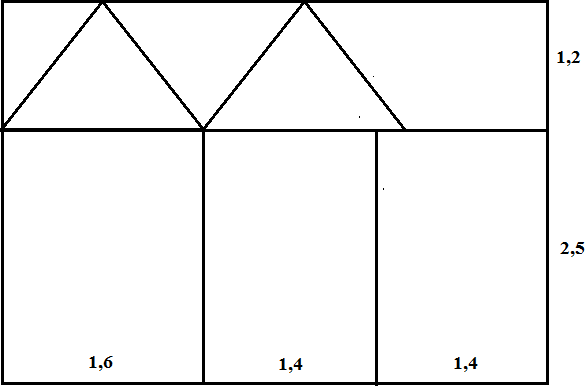 | 1 | |
| 4,4 м | 1 | | |
| 4 c | 2,53 или1, 4 4 или1, 6 2 | 1 | За любое из произведений |
| 16,3 | 1 | |