Файл: Спецификация суммативного оценивания за четверть по предмету Геометрия.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 224
Скачиваний: 1
СОДЕРЖАНИЕ
Уровни мыслительных навыков по предмету «Геометрия»
Распределение проверяемых целей по уровням мыслительных навыков в разрезе четвертей
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 1 ЧЕТВЕРТЬ
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 1 четверть
Образец заданий и схема выставления баллов
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 2 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 2 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 2 четверть
Образец заданий и схема выставления баллов
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 3 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 3 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 3 четверть
Образец заданий и схема выставления баллов
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 4 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 4 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 4 четверть
-
Параллельно оси цилиндра проведено сечение, площадь которого равна S, а диагональ сечения образует с плоскостью основания угол . Сечение пересекает нижнее основание цилиндра по хорде, которую видно из центра этого основания под углом .
Выполните рисунок по условию задачи. Найдите:
-
высоту цилиндра;
-
радиус основания цилиндра.
[3]
[2]


 Схема выставления баллов
Схема выставления баллов | № | Ответ | Балл | Дополнительная информация |
| 1 a | 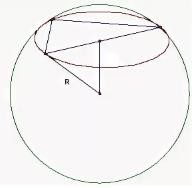 | 1 | Выполнен рисунок по условию задачи |
| 1 b | Показано, что центр сечения совпадает с серединой гипотенузы треугольника. Показан метод нахождения искомого расстояния. | 1 | |
| 4 2 | 1 | | |
| 2 | 135 122 360 | 1 | За использование формулы площади кругового сектора |
| 54 | 1 | | |
| r12 54 | 1 | Балл выставляется со своимзначением площади кругового сектора | |
| r 4, 5 | 1 | | |
| 3 | Высота цилиндра 24 см, радиус основания 2 см | 1 | |
| 4 24 4 | 1 | За использование формулы площадей круга и прямоугольника | |
| 2,12 1, 5 4, 2 | 1 | ||
| 110, 71 | 1 | | |
| 4 | Выполнен рисунок по условию задачи | 1 | |
| Радиус верхнего основания равен 4 | 1 | | |
| Радиус нижнего основания равен 8 | 1 | | |
| Sполн. 176 | 1 | | |
| 5 a | Выполнен рисунок по условию задачи, указаны углы из условия задачи | 1 | |
| Показан метод нахождения высоты цилиндра | 1 | | |
| S tg | 1 | | |
| 5 b | Показан метод нахождения радиуса цилиндра | 1 | |
| S ctg 2 sin 2 | 1 | | |
| Итого: | 20 | | |
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 4 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 4 четверть
Продолжительность – 40 минут
Количество баллов – 20
Типы заданий:
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 5 заданий, включающих вопросы с кратким и развернутым ответами.
В вопросах, требующих краткого ответа, обучающийсяз аписывает ответ в виде численного значения, слова или короткого предложения.
В вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов.
24
Характеристика заданий суммативного оценивания за 4 четверть
| Раздел | Проверяемая цель | Уровень мыслительных навыков | Кол. заданий * | № задания* | Тип задани я* | Время на выполнение, мин* | Балл* | Балл за раздел | |
| Объемы тел | 11.3.18 - решать задачи практического содержания на комбинации геометрических тел | Применение | 2 | 1 a,b,c | КО/РО | 10 мин | 5 | 20 | |
| 3 | РО | 10 мин | 5 | ||||||
| 11.3.15 - знать формулы нахождения объемов конуса и усеченного конуса и применять их при решении задач | Применение | 1 | 1 c | РО | 4 мин | 2 | |||
| 11.3.13 - знать формулы нахождения объема пирамиды и усеченной пирамиды и применять их при решении задач | Применение | 1 | 2 | РО | 8 мин | 4 | |||
| 11.3.12 - знать формулу нахождения объема призмы и применять ее при решении задач | Применение | 1 | 4 | РО | 8 мин | 4 | |||
| ИТОГО: | | | 5 | | | 40 мин | 20 | 20 | |
| Примечание:*-разделы,вкоторыеможновноситьизменения | |||||||||
25
Образец заданий и схема выставления баллов
Задания суммативного оценивания за 4 четверть по предмету «Математика»
-
Дан металлический шар радиусом 15 см. а) Найдите объем данного шара.
[1]
-
Этот шар положили в цилиндрический контейнер радиусом 25 см и высотой 60 см. После этого контейнер наполнили водой.
Рассчитайте объем воды, потребовавшейся для наполнения контейнера.
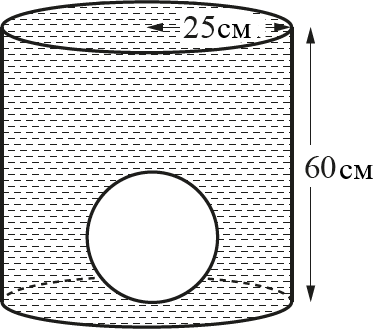
[2]
-
Затем шар достали из контейнера. Какова глубина воды, оставшейся в контейнере?
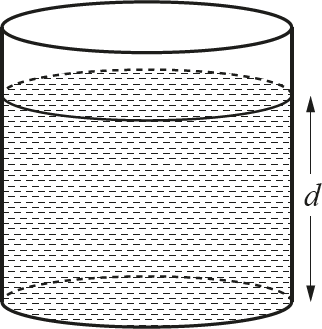
[2]
-
Металлический шар переплавили в конус высотой 54 см. Найдите радиус конуса.
(Ответокруглитедодесятых)
-
SABC- пирамида.
SA ABC ,
SA 4
см,
[2]
BC 8 см, двугранный угол при ребре
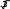 BC равен 45 . Выполнив рисунок, вычислите объем пирамиды.
BC равен 45 . Выполнив рисунок, вычислите объем пирамиды.[4]
3.
-
Садовник вырыл траншею шириной 1,4 м, длиной 200 м и глубиной 0,8 м. Найдите объем траншеи.
[1]
26
-
В траншею поместили трубу, радиусом 0,25 м и длиной 200 м. Найдите объем трубы