Файл: Diskretnaya_matematika.doc

.

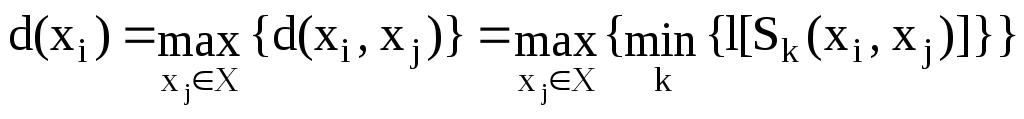В качестве примера рассмотрим схему первой (1870 г.) сети связи для почтовых голубей (рис. 3.29).

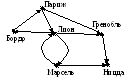
Рис. 3.29. Схема первой сети связи для почтовых голубей

Граф, пред­став­ляющий ее, изображен на рис. 3.29, а матрица отклонений и вектор отклоненностей – в табл. 3.2 и табл. 3.3 соответственно.

Таблица 3.2. Отклонения d(x_i,x_j)

Таблица 3.3. Вектор отклонений

Для неориентированного графа, соответствующего графу, изо­браженному на рис. 3.29, можно найти аналогичные характеристики, но без учета ориентации дуг. При этом матрица d(x_i,x_j) оказывается симметричной.

В связном неориентированном графе понятиям отклонения и отклоненности соответствуют понятия: расстояниеиудаленность.

Пусть G(X) – связный неориентированный граф. В соответст­вии с определением связности для вершинx_iиx_jграфа существует элементарная цепьS(x_i,x_j) с концамиx_iиx_j, причемl(S)0.

Расстояниемd(x_i,x_j) между вершинамиx_iиx_jназывается дли­на цепиS(x_i,x_j) наименьшей длины

.

Удаленность вершины x_i графа G(X) есть число

.

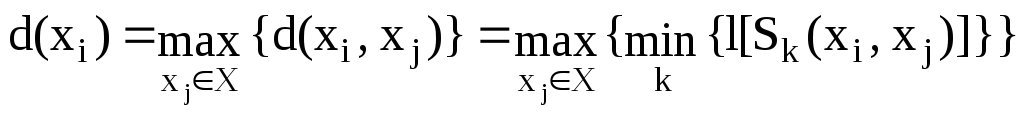Центромграфа называется вершина, в которой достигается наименьшая из отклоненностей (удаленностей), если таковая являет­ся конечным числом. В графе может быть несколько центров (Париж, Лион), а может не быть ни одного.

Периферийной вершинойграфа называется вершина с наи­большей отклоненностью или удаленностью (Гренобль, Ницца).

Радиусомp(G) ориентированного графа называется отклоненность его центра.

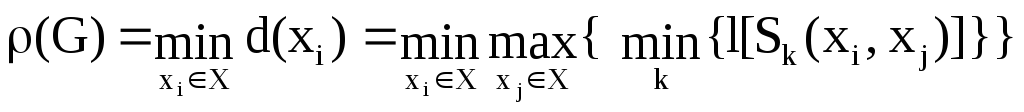
В примере (рис. 3.29) (G) = 2 (d(П) =d(Л) = 2). Если в графе нет центров, то полагают, что(G) =. В неориентированном графе(G) – удаленность центра.

Диаметромнеориентированного графа называется удален­ность периферийной вершины.

3.6.2. Характеристические числа графов

Решение многих технических задач методами теории графов сводится к определению тех или иных характеристик графов, поэто­му полезно знакомство со следующими характеристиками.

Цикломатическое число. Пусть G(X) – неориен­тирован­ный граф, имеющий n вершин, m ребер и k компонент связности. Цикломатическим числом графа G называется число µ(G) = m - n + k.

Это число имеет интересный физический смысл: оно равно наибольшему числу базисных (независимых) циклов в графе. При расчете элек­трических цепей цикломатическим числом можно пользоваться дляопределения числа независимых контуров.

Хроматическое число. Пусть р – натуральное число. Граф G(X) называется р-хроматическим, если его вершины можно рас­красить различными цветами так, чтобы никакие две смежные вер­шины не были раскрашены одинаково. Наименьшее число р, прикотором граф является р‑хроматическим, называется хроматическим числом графа и обозначается γ(G).

Если γ(G) = 2, то граф называется бихроматическим. Необходимым и достаточным условием того, чтобы граф был бихроматическим, является отсутствие в нем циклов нечетной длины.

Хроматическое число играет важную роль при решении задачи наиболее экономичного использования ячеек памяти при програм­мировании. Однако его определение, за исключением γ(G) = 2, пред­ставляет собой довольно трудную задачу, требующую применения ЭВМ.

Множество внутренней устойчивости. Множество S  X графа G(X) называется внутренне устойчивым, если никакие две вершины из S не являются смежными, то есть для любого х  S имеет место:

G(x)  S = .

Множество внутренней устойчивости, содержащее наибольшее число элементов, называется наибольшим внутренне устойчивым множеством, а число элементов этого множества называется чис­лом внутренней устойчивости графа G. Наибольшее внутренне устойчивое множество играет важную роль в теории связи.

Множество внешней устойчивости. Множество Т  X графа G(X) называется внешне устойчивым, если любая вершина, не при­надлежащая Т, соединена дугами с вершинами из Т, то есть для лю­бого х  Т имеет место: G(x)  Т  .

Множество внешней устойчивости, содержащее наименьшее число элементов, называется наименьшимвнешне устойчивым множеством, а число элементов этого множества называетсячис­лом внешней устойчивостиграфаG(X).

3.7. Циклы и разрезы графа

3.7.1. Остов и кодерево

ОстовомT графаGназывается называется подграф графа в виде дерева, содержащий все его вершины. Остов определяет каркас графа.Кодеревом T^* остова Т называется подграф графаG, содержащий все вершины и только те ребра, которые не входят в остов Т. Ребра остова называют ветвями, а ребра кодерева - хордами.

Из определений остова и кодерева следует:

1. Объединение остова T и кодерева T^* есть граф G:

Т T^* = G.

2. Кодерево есть дополнение остова T до графа G:

T^*=G\ Т =Т.

Рассмотрим пример графа, изображенного на рис. 3.30.

Р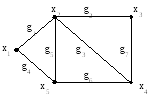ис. 3.30. Граф

Выберем остов графа в виде связного дерева (рис. 3.31).

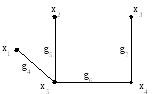
Рис. 3.31. Остов графа

Кодерево для данного остова имеет вид несвязного графа (рис. 3.32), но он может быть и связным.

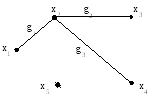
Рис. 3.32. Кодерево графа