ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.08.2024
Просмотров: 411
Скачиваний: 0
СОДЕРЖАНИЕ
Теории управления квантовыми системами.
1. Основные понятия и определения квантовой механики
1.1. Чистые и смешанные состояния
2. Элементы квантовой теории информации
2. 3. Преобразование одного кубита
2.5. Перепутывание и квантовая неразличимость
2.6. Логический элемент «управляемое не»
3. Парадокс эйнштейна – подольского – розена (эпр)
5.4 Понятие о квантовой криптографии
5.4.1. Защита посредством неортогональных состояний
5.4.2. Защита посредством перепутывания
5.4.3. Практическая реализация квантово – криптографических систем
6.2. Протокол квантовой телепортации
6. 3. Обзор некоторых экспериментальных результатов по квантовой телепортации
6.4. Заключительные замечания: возможна ли телепортация макрообъекта?
7. Квантовые вычисления. Квантовые компьютеры.
7.4.2. Моделирование вероятности
7.4.3. Алгоритм разложения на простые множители или алгоритм Шора
7.5. Общие требования к квантовым компьютерам Практическая реализация
Таким образом,
если было бы возможным копирование, то
Боб мог бы идентифицировать с произвольно
высокой вероятностью успеха какое из
двух состояний
![]() или
или![]() было приготовлено Алисой и, таким
образом, достижимая информация была быН(p).
было приготовлено Алисой и, таким
образом, достижимая информация была быН(p).
Скрытая природа квантовой информации играет центральную роль в мощности квантовых вычислений и достижимая информация есть количественное проявление природы квантовой информации. К сожалению, не существует общего рецепта вычисления достижимой информации. В то же время имеется ряд важных достижимых границ, которые строго обоснованы. Наиболее важная из них - граница Холево. Она играет очень важную роль в теории квантовой информации.
Теорема о границе Холево
Предположим, что Алиса приготавливает состояние Х, где Х = 0,...n с вероятностями p0,...pn. Пусть Боб выполняет некое измерение этого состояния, дающее максимальное относительно всех вероятностных мер значение взаимной информации описываемое множеством элементов {Ey} = {E0,...,Em}. Результат измерения Боба есть Y. Граница Холево утверждает, что при любых измерениях Боб может достигнуть:
![]()
где
![]()
Таким образом, граница Холево является верхней границей достижимой информации.
Граница Холево играет ключевую роль при доказательстве многих положений квантовой теории информации. Рассмотрим несколько примеров.
Пример 1. В теории квантовой информации доказывается теорема (см.**), что
![]() (2.23)
(2.23)
где равенство
достигается только для тех состояний
![]() ,
которые имеют ортогональные основания
(т.е. определены на множестве ортогональных
состояний). Здесь
,
которые имеют ортогональные основания
(т.е. определены на множестве ортогональных
состояний). Здесь![]() аpx
- набор вероятностей для состояний
аpx
- набор вероятностей для состояний
![]() (
т.е.
(
т.е.![]() ).
Предположим, что неравенство в (2.23) -
строгое. Тогда, из теоремы о границе
Холево сразу следует, чтоH(X:Y)
строго меньше H(X).
Следовательно невозможно достоверно
определить X,
исходя из результатов измерений Y.
Это обобщает наше понимание того, что
если состояния, приготавливаемые Алисой
неортогональны, то Боб не может определить
с достоверностью, какое состояние было
приготовлено Алисой.
).
Предположим, что неравенство в (2.23) -
строгое. Тогда, из теоремы о границе
Холево сразу следует, чтоH(X:Y)
строго меньше H(X).
Следовательно невозможно достоверно
определить X,
исходя из результатов измерений Y.
Это обобщает наше понимание того, что
если состояния, приготавливаемые Алисой
неортогональны, то Боб не может определить
с достоверностью, какое состояние было
приготовлено Алисой.
Пример 2.
Пусть Алиса
приготавливает единичный кубит в одном
из двух квантовых состояний, в соответствии
с результатом подбрасывания монеты.
При выпадении орла Алиса готовит
состояние |0>, если же выпадает решка,
то она готовит состояние
![]() ,
где
- некоторый действительный параметр.
Цель Боба - определить какое из двух
состояний было послано.
,
где
- некоторый действительный параметр.
Цель Боба - определить какое из двух
состояний было послано.
В базисе |0>, |1> состояние можно записать следующим образом:
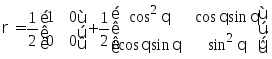
Чтобы вычислить
границу
![]() ,
найдемS().
Для этого найдем собственные значения
матрицы :
,
найдемS().
Для этого найдем собственные значения
матрицы :
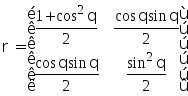
Уравнение на собственные значения:
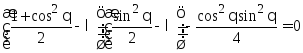
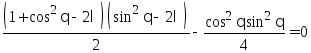
![]()
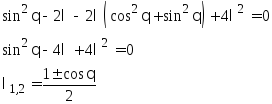
Тогда
![]() :
:
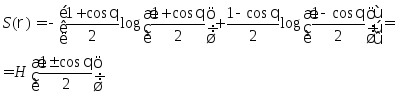
Теперь найдем
величину
![]() .
Собственные значения каждой из двух
матриц плотности равны
.
Собственные значения каждой из двух
матриц плотности равны![]() (0,
1) и
(0,
1) и![]() ,
поэтому
,
поэтому
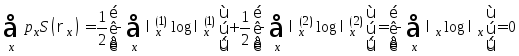
Отсюда, граница
Холево определяется бинарной энтропией
Шеннона
![]() .
Из рисунка видно, что максимум границы
достигается при
= /2
и отвечает уровню 1 бит.
.
Из рисунка видно, что максимум границы
достигается при
= /2
и отвечает уровню 1 бит.
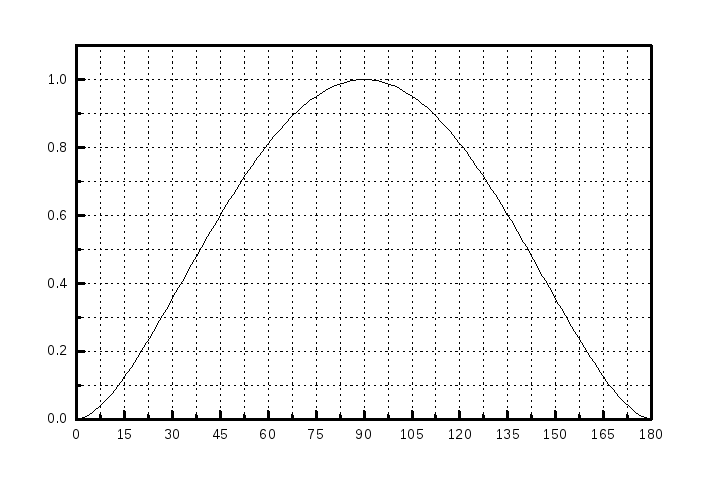
По вертикали отложено значение границы Холево (фактически - это бинарная энтропия), по горизонтали - значение параметра в град.
Это, в свою очередь, означает, что Алиса готовит состояния, которые выбирает из ортогонального набора |0> либо |1> с равной вероятностью. Значит, Боб может достоверно определить какое из состояний было приготовлено Алисой. Для других значений граница Холево строго меньше единицы, т.е. Боб не может определить достоверно, какое из неортогональных состояний было приготовлено. С другой стороны, ясно, что при = 90 два состояния неразличимы. Поэтому при этом значении параметра Боб может угадать, какое состояние было послано с вероятностью 50%.
Границу (или
информацию Холево) можно ввести несколько
по-другому. Переобозначим величины,
входящие в это определение:
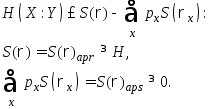
Первая величина называется априорной (безусловной) энтропией. Она описывается соответствующими диагональными элементами матрицы плотности. Апостериорная (условная) энтропия определяет вносимую каналом связи ошибку в классической схеме. В квантовой теории она отвечает за квантовую недетерминированность сигналов, связанную с соотношением неопределенности. В отсутствие классических шумов и помех апостериорная энтропия обращается в нуль. Сигналы на входе и на выходе канала при этом коррелированы и взаимная информация I() = S = H.
Достижимая информация определяется выражением Iacc = S() = H, что соответствует случаю, когда сигнал формируется из ортонормированных собственных состояний n, а операторы на выходе коммутируют с оператором плотности, т.е. когда S()aps = H()aps = 0.
В случае, когда
сигналы
![]() - это чистые состояния с нулевой энтропией,
граница Холево просто сводится к
утверждению, что
- это чистые состояния с нулевой энтропией,
граница Холево просто сводится к
утверждению, что
![]() ,
,
где
![]() - оператор плотности для ансамбля чистых
сигналов (состояний). И хотя Шенноновская
энтропияH(Х)
сообщения, посылаемого источником в
общем случае больше, чем энтропия фон
Неймана
- оператор плотности для ансамбля чистых
сигналов (состояний). И хотя Шенноновская
энтропияH(Х)
сообщения, посылаемого источником в
общем случае больше, чем энтропия фон
Неймана
![]() ансамбля сигналов, достижимая информация
(классическая) ограничена величиной
ансамбля сигналов, достижимая информация
(классическая) ограничена величиной![]() .
Таким образом ясно, что граница Холево
устанавливает связь между энтропией
фон Неймана квантового ансамбля и
(классической)
взаимной Шенноновской информацией
квантового
канала связи.
.
Таким образом ясно, что граница Холево
устанавливает связь между энтропией
фон Неймана квантового ансамбля и
(классической)
взаимной Шенноновской информацией
квантового
канала связи.
Такая связь, однако,
является довольно слабой. Дело в том,
что теорема Холево формулируется в виде
неравенства. Поэтому, в принципе, можно
сконструировать такой источник квантовых
сигналов, для которого взаимная информация
Н(X:Y)
и близко не достигает
![]() при любом выборе наблюдаемойY
при декодировании. Поэтому, хотя из
теоремы Холево и следует
информационно-теоретическое значение
величины
при любом выборе наблюдаемойY
при декодировании. Поэтому, хотя из
теоремы Холево и следует
информационно-теоретическое значение
величины
![]() ,
она не дает интерпретации
,
она не дает интерпретации![]() в терминах классической теории информации.
Например, мы не могли бы использовать
теорему Холево при интерпретации
квантовой теории некоторого макросостояния
термодинамической системы, как дающую
меру ресурсов, необходимых для
представления информации о микросостояниях
системы.
в терминах классической теории информации.
Например, мы не могли бы использовать
теорему Холево при интерпретации
квантовой теории некоторого макросостояния
термодинамической системы, как дающую
меру ресурсов, необходимых для
представления информации о микросостояниях
системы.
Ответ на этот
вопрос дает квантовая теорема кодирования
Б.Шумахера (1995). В ней классическая идея
о двоичной логике в терминах битов
заменяется моделью квантовых битов -
двухуровневых систем. Эти квантовые
биты являются фундаментальными единицами
квантовой информации. В теореме
утверждается, что энтропия
фон Неймана
![]() ансамбля является просто средним числом
кубитов, необходимых для кодирования
состояний ансамбля при помощи идеальной
кодирующей системы.
Теорему можно рассматривать как
краеугольный камень альтернативного
подхода в квантовой теории информации.
Вместо использования классической
теории информации к вероятностям,
вычисленным по законам квантовой
механики (подход Левитина и Холево), мы
пересмотрим понятия кодирования и мер
информации, которые сами по себе
определенно являются квантовыми
величинами.
ансамбля является просто средним числом
кубитов, необходимых для кодирования
состояний ансамбля при помощи идеальной
кодирующей системы.
Теорему можно рассматривать как
краеугольный камень альтернативного
подхода в квантовой теории информации.
Вместо использования классической
теории информации к вероятностям,
вычисленным по законам квантовой
механики (подход Левитина и Холево), мы
пересмотрим понятия кодирования и мер
информации, которые сами по себе
определенно являются квантовыми
величинами.
Теорема о квантовом кодировании при отсутствии шума
Пусть М
- источник квантового сигнала, который
представляется ансамблем. Этот ансамбль
описывается оператором плотности
![]() .
Пусть имеются два числа
.
Пусть имеются два числа
![]() .
.
Предположим, что имеется
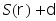 кубитов. Тогда для достаточно большого
N
(N
-это число
независимых испытаний с функцией
распределения pn)
группы из N
сигналов из источника М
могут быть переданы с помощью имеющегося
набора кубитов с качеством F
> 1 -
кубитов. Тогда для достаточно большого
N
(N
-это число
независимых испытаний с функцией
распределения pn)
группы из N
сигналов из источника М
могут быть переданы с помощью имеющегося
набора кубитов с качеством F
> 1 -
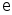 .
.Предположим, что имеется
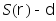 кубитов.
Тогда для достаточно большого N,
при передаче групп из N
сигналов от источника с помощью
имеющегося набора кубитов, качество
передачи будет F
<
кубитов.
Тогда для достаточно большого N,
при передаче групп из N
сигналов от источника с помощью
имеющегося набора кубитов, качество
передачи будет F
<
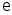 .
.
Энтропию фон
Неймана ансамбля сигналов (чистых
состояний) можно интерпретировать как
число кубитов на сигнал, необходимое
для передачи с качеством, близким к
единице. Если имеется больше, чем
![]() кубитов, при увеличении группы сигналов
можно добиться произвольно высокого
качестваF.
Если же доступно меньше, чем
кубитов, при увеличении группы сигналов
можно добиться произвольно высокого
качестваF.
Если же доступно меньше, чем
![]() кубитов, качествоF
стремиться к нулю.
кубитов, качествоF
стремиться к нулю.
Более того,
![]() является в некотором смысле количеством
кубитов, необходимым для передачи части
перепутанной системы при поддержании
качестваF
всего состояния близким к единице.
является в некотором смысле количеством
кубитов, необходимым для передачи части
перепутанной системы при поддержании
качестваF
всего состояния близким к единице.
Таким образом, энтропия S является мерой физических ресурсов, необходимых для представления информационного содержания о системе смешанных состояний. Неважно каким образом получена эта система смешанных состояний - из стохастического процесса или при выбрасывании части перепутанных состояний. Квантовая энтропия фон Неймана измеряется в кубитах.
Перенос квантовой информации. Понятие квантового канала связи.
В квантовой теории информации необходимо различать понятия копирования состояний и перенос информации из системы М в систему Х. При переносе состояние системы М передается к системе Х без сохранения копии начального состояния:
![]()
где
![]() и
и![]() - некоторые “нулевые” состояния системХ
и М.
После переноса сигнал полностью возникает
в кодирующей системе Х,
исчезая в системе М.
Одним из примеров переноса служит
явление квантовой телепортации.
- некоторые “нулевые” состояния системХ
и М.
После переноса сигнал полностью возникает
в кодирующей системе Х,
исчезая в системе М.
Одним из примеров переноса служит
явление квантовой телепортации.
Перенос является унитарной операцией для произвольных состояний из системы М. Это обеспечивает сохранение скалярного (внутреннего) произведения:
![]() для любых сигналов
(состояний)
для любых сигналов
(состояний)
![]() и
и![]() .
Это может происходить только, если
размерность гильбертова пространства
системыХ
X
не меньше
чем размерность гильбертова пространства
системы М
M.
Как происходит процесс переноса с
помощью унитарного преобразования U?
Для ответа на этот вопрос необходимо
понять как ортогональный базис из
гильбертова пространства системы М
переходит в ортогональный базис
гильбертова пространства системы Х.
После этого эволюция других состояний
будет очевидна из-за линейности.
.
Это может происходить только, если
размерность гильбертова пространства
системыХ
X
не меньше
чем размерность гильбертова пространства
системы М
M.
Как происходит процесс переноса с
помощью унитарного преобразования U?
Для ответа на этот вопрос необходимо
понять как ортогональный базис из
гильбертова пространства системы М
переходит в ортогональный базис
гильбертова пространства системы Х.
После этого эволюция других состояний
будет очевидна из-за линейности.
Перенос является обратимой операцией, поскольку состояние сигнала может быть передано назад из Х в М посредством унитарного преобразования U-1. Поэтому система связи, основанная на переносе, представляется в следующем виде. Со стороны кодирования, сигнал (квантовое состояние), исходящий из системы М, поступает в процессе унитарного преобразования U в кодирующую систему Х. Система Х переправляется от передатчика к получателю. С декодирующей стороны выполняется унитарное преобразование U-1 для возвращения сигнала из Х в М* - как идентичной копии системы М. В символьном виде: