Файл: Исаев Г Н Теоретико-методологические основы качества информационных систем.doc

Дефекты ИС могут быть заданы случайными величинами, каждая из которых характеризуется временем и (или) стоимостью обнаружения и исправления дефекта и отображаемые статистической структурой в соответствии с формулами (3.9) и (3.10). Исходя из характера ИС, наиболее приемлемым представляется провести сбор данных выборочно комбинированным методом. По каждому этапу должны быть взяты репрезентативные выборки серий обрабатываемых документов. В целях обеспечения репрезентативности, в частности, относительно запаздывания документов, сбор сведений можно выполнить с использованием технологических журналов регистрации поступления документов (пачек документов) по этапам, если таковые имеются в наличии. При условии сбора и регистрации сведений статистические данные о состоянии ИС подвергаются обработке на ЭВМ. Выбор пакета прикладных программ определяется целями оценки, характером решаемых задач, имеющимся парком ЭВМ и набором имеющихся пакетов.

Классификация дефектов и получение на этой основе состава и содержания показателей качества ИС могут быть выполнены методом агломеративного кластер-анализа посредством реализации соответствующих программ с применением ЭВМ. Исходя из существа кластер-анализа, дефекты, оказавшиеся в одной группе, должны быть сходными между собой, а дефекты, принадлежащие разным классам, разнородными, относящимися к различным ветвям дерева классификации. Критерием разнородности выберем некоторую метрику, посредством которой дефекты могут быть объединены в некоторый класс по количественному критерию сходства (различия) классифицируемых дефектов. Можно использовать различные критерии, например, евклидово расстояние [118,141,188]. Определение состава первичных показателей качества ИС выполним посредством агломеративного кластер-анализа. По существу кластер-анализа, дефекты, сходные между собой, должны быть в одной группе, а дефекты, принадлежащие разным классам, разнородными, относящимися к разным ветвям дерева классификации.

Пусть множество D={ } отображает выборку, состоящую из дефектов, регистрируемых по этапам ИС. Имеется некоторое множество характеристик G={ }, присущих каждому из . Количественное измерение j–ой характеристики дефекта обозначим , тогда вектор =[ ] размерности mx1 будет соответствовать каждому ряду измерений для каждого . Отсюда множество дефектов D располагает множеством векторов измерений , которые характеризуют множество D. Отметим, что множество D может быть отображено как n точек в p–мерном пространстве . Задача кластеризации дефектов заключается в том, чтобы для анализа некоторого целого числа S (s < n) на основе Х разбить множество D на конечное число подмножеств

(3.17)

где , так, чтобы
, i,j (3.18)

. (3.19)

Отправной точкой для определения состава и содержания показателей качества ИС является получение укрупненных классов дефектов, сформированных в результате кластеризации. Априори можно предположить, что в результате будут получены классы дефектов соответствующих оценкам по достоверности, полноте, своевременности и др.

Для дальнейшего рассмотрения существа иерархической агломеративной классификации статистической структуры дефектов ИС с учетом подходов к кластер-анализу, изложенных в [20,51,67,76,98], конкретизируем обозначения дефектов и процесс их кластеризации: - элементы (дефекты) матрицы исходных данных Х (ведомость дефектов), где i=1,2,..,n – номер строки (шифр, код дефекта), j=1,2,…,m - номер столбца (шифр, код признака - время и/или стоимость обнаружения и исправления дефекта); - среднее значение признака для n дефектов (среднее по столбцу j), определяемое по формуле

= (3.20)
-среднее квадратическое отклонение признака x_j, определяемое по формуле

(3.21)

затем определяется – нормированный элемент матрицы Х

=( )/ (3.22)
после чего матрица дефектов Х заменяется матрицей Z. Затем вычисляются всевозможные расстояния - квадрат евклидова расстояния между дефектами i и k.

= . (3.23)
После подсчета расстояния для всех пар дефектов матрица Z заменяется симметричной матрицей Q (матрица расстояний). На основе этой матрицы проводится кластеризация. Вначале кластеризации каждый дефект обозначается как отдельный кластер. На первом шаге кластеризации определяется пара дефектов, расстояние d_ij между которыми минимально. Эти дефекты объединяются в один кластер, в матрице расстояний «вычёркиваются» строка и столбец, соответствующие первому из этих дефектов. Затем матрица расстояний рассчитывается вновь, так как расстояние пары дефектов нового будущего кластера может измениться относительно оставшихся в матрице расстояний дефектов.

На втором шаге процедуры в матрице расстояний, уменьшенной на одну строку и один столбец, снова определяется минимальное расстояние и формируется новый кластер. Этот кластер может быть сформирован в результате объединения либо двух дефектов, либо одного дефекта с кластером, сформированном на первом (предыдущем) шаге. Снова в матрице расстояний вычёркивается одна строка и один столбец, снова пересчитывается матрица расстояний и т.д. После выполнения каждого шага число кластеров уменьшается на единицу, а матрица расстояний уменьшается на одну строку и один столбец.

Алгоритм заканчивает работу тогда, когда все дефекты будут объединены в один общий кластер, т.е. при условии сформирования ствола дерева классификации. При получении на ЭВМ распечатки дендрограммы можно будет путем анализа выявить состав и свойства классов дефектов. С учетом состава и свойств сформированных классов дефектов будут определяться показатели качества ИС. Более расширенное рассмотрение кластер-анализа статистической структуры дефектов ИС представлено в [98, 140].

Полученные в результате кластеризации однородные статистические структуры должны быть подвергнуты дальнейшей обработке на ЭВМ с целью получения статистических параметров, в частности, средних выборочных, среднеквадратических отклонений, оценок параметров в виде доверительных интервалов, выполняемых по векторам времени и стоимости. Кроме того, могут быть определены также типы эмпирических распределений случайных величин по времени и стоимости, наиболее согласующиеся с теоретическими [188].

В результате дальнейшей обработки должны быть получены оценки математического ожидания по времени и по стоимости относительно классов дефектов. Для этого потребуется определить также количество дефектов по их видам и этапам, на которых они зарегистрированы. Кроме того, на ЭВМ должны быть обработаны данные по причинам-факторам, обусловившим возникновение дефектов.

В результате измерения и обработки данных на ЭВМ получится определенный объем информации о качестве ИС. Затем, с целью рационализации дальнейшей работы, информацию о качестве необходимо представить в удобной для восприятия форме, т.е. в виде набора унифицированной технологической документации.

3.3. Модель расчета значений показателей оценки качества информационных систем

Исходной точкой для определения состава и содержания показателей качества ИС является получение укрупненных классов дефектов, задаваемых в результате кластер-анализа. Априори можно предположить, что в результате получены классы дефектов соответственно по достоверности, полноте, своевременности. Определение конкретных формул для расчета значений показателей оценки качества ИС можно выполнить с учетом методологических положений, концептуальной модели, а также формул (3.9-3.16) принципиальной модели СКИС.

Определим понятие «значение показателя достоверности информации - это величина противоположная вероятности ошибки в определенном объеме информации». В соответствии с вышерассмотренной математической моделью вероятность ошибки представляется как отношение числа дефектов к определенному объему информации. Отсюда значение достоверности можно рассчитать по формуле

(3.24)
где – значение единичного фактического показателя достоверности информации i–го вида на j–м этапе обработки ( ); - количество обнаруженных ошибочных символов (дефектов) в информации i–го вида на j–м этапе обработки; - объем информации в символах, содержащейся в информации i–го вида

на j–м этапе.

Теперь определим понятие «значение показателя полноты информации - это величина противоположная вероятности пропуска единицы информации в определенном объеме информации» и это значение рассчитаем по формуле

(3.25)

где – значение единичного фактического показателя полноты информации в документации i–го вида на j–м этапе обработки ( ); -количество отсутствующих показателей, регламентированных форматом документа i–го вида на j–м этапе; - количество показателей в документах i-го вида, обрабатываемых на j-м этапе.

Определим также и понятие «значение показателя своевременности информации - это величина противоположная вероятности запаздывания информации относительно регламентного объема информации, предназначенного к выдаче пользователю на заданное время». Значение этого показателя можно рассчитать по формуле

(3.26)
где – значение единичного фактического показателя своевременности обработки информации (документации) i–го вида на j–м этапе обработки ( ); -фактическое количество документов (пачек документов) i–го вида, выданных с опозданием, j-м этапе обработки; -общее количество документов (пачек документов) i-го вида, необходимое к выдаче по регламенту на заданное время на j–м этапе .

Тогда значения групповых показателей достоверности, или полноты, или своевременности по все этапам и/или по всем видам информации (документации) можно определить по формуле

(3.27)
где – значение группового фактического показателя 1-го вида ( ); -значение единичного фактического показателя 1-го вида (достоверность, полнота, своевременность и др.); l, i, j, - индексы соответственно видов показателей, документации и этапов обработки.

В роли базовых значений принимается вероятность одного дефекта соответственно по достоверности, полноте, своевременности относительно соответствующих объемов обрабатываемой документации. При данном условии значение базового показателя определяется по формуле

(3.28)
где – значение базового показателя 1-го вида ( ); -объем обрабатываемой документной информации i–го вида; 1- индекс показателя.

В зависимости от вида показателя – достоверности, полноты, своевременности, объем информации измеряется соответственно в символах, показателях, документах.

Оценку относительного уровня качества можно выполнить по значению относительных показателей, отображаемых как отношение фактических показателей к базовым, и определяемых по формуле

(3.29)
где – значение относительно уровня показателя 1-го вида ( ); -значение фактического показателя 1-го вида; -значение базового показателя 1-го вида.

С учетом обратно функциональной зависимости значение относительного показателя качества по себестоимости и принятого нами принципа унификации измерения (раздел 2.2) указанное значение определяется по формуле

(3.30)
где с- индекс показателя себестоимости, остальные значение эквивалентны соответствующим значениям формулы (3.29).

Исходя из иерархичности свойств объектов и содержания оценки КИС, интегральные показатели определяются как средневзвешенные величины по набору значений показателей в целом - единичных, групповых, базовых и относительных.

Интегральный показатель по набору единичных показателей определяется по формуле

(3.31)
где – интегральный показатель по набору единичных показателей достоверности, полноты, своевременности ( ); - единичный фактический показатель 1-го вида. И далее определяем

(3.32)
где – интегральный показатель по набору групповых показателей ( ); - групповой показатель 1-го вида,
(3.33)
где – интегральный показатель по набору базовых показателей ( ); - базовый показатель 1-го вида,
(3.34)
где – интегральный показатель по набору относительных показателей ( ); - относительный показатель 1-го вида.

3.4. Модель определения обобщенных показателей и коэффициентов их весомости

При расчете обобщенных показателей целесообразно использовать функциональную зависимость между дефектами обработки и значениями обобщенных показателей. С учетом использования расчетно-аналитических методов оценки качества ИС указанную зависимость можно определить на основе регрессионной зависимости. При этом выбор вида функции обобщенного показателя от единичных (групповых) показателей должен быть выполнен так, чтобы получаемая при этом линейная зависимость была бы лучшей аппроксимацией функциональной зависимости. Кроме того, при расчете значений обобщенных показателей необходимо определить значения коэффициентов весомости показателей, в роли которых выступают коэффициенты регрессии [96,211].

С учетом существа рассматриваемой задачи в нашем случае целесообразно в качестве модели зависимости использовать регрессионные уравнения линейного вида. При этом обобщенными показателями будут производительность ИС и себестоимость обработки одного документа. Используемыми переменными выступают здесь время и стоимость обнаружения и исправления дефектов соответственно по достоверности, полноте, своевременности, а возможно и по другим категориям.

Для определения значений обобщённых показателей качества и коэффициентов весомости независимых переменных может быть принята модель множественной линейной регрессии

(3.35)
где – зависимая (прогнозируемая) переменная – производительность и (или) себестоимость; - независимые (прогнозирующие) переменные (значения времени или стоимости обнаружения и исправления дефектов соответственно по достоверности, полноте, своевременности); - свободный член регрессии; -вектор оценок коэффициентов линейной регрессии; - случайные величины (совокупность латентных случайных факторов).

Оценка параметров , , производится методом наименьших квадратов, то есть из условия минимума суммы квадратов отклонений значений

(3.36)

Это приводит к системе нормальных уравнений

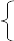
= (3.37)

,

где =(,…, - вектор оценок коэффициентов линейной регрессии, а величина - свободным членом уравнения регрессии; - обратная матрица ковариаций между переменными ; - вектор оценок ковариаций между переменными у и переменными ; - оценка среднего значения у; - вектор средних значений переменных .