Файл: Исаев Г Н Теоретико-методологические основы качества информационных систем.doc

координат до пересечения с линией регрессии. Подобным образом можно определить экспресс-оценки по графику регрессии себестоимости обработки документов (рис. 4.6).

Для получения значений обобщенных показателей качества в результате реализации программы регрессионного анализа были получены коэффициенты регрессии и оценочные величины соответственно по производительности и себестоимости (таблицы 4.9 и 4.10). По этим данным составлены уравнения множественной линейной регрессии по производительности и по себестоимости:

= 348,9 – 1,452 x₁ - 0,1119 x₂ + 0,07146 x₃.

= 3,66 + 0,3924 x₁ + 0,0002067 x₂ - 0,02332 x₃.

В правой части уравнений расположены слева направо соответствующие свободные члены регрессии (нулевые коэффициенты), затем коэффициенты регрессии. Они обозначают соответственно значения базовых показателей производительности и себестоимости и коэффициентов весомости по достоверности, полноте и своевременности. Подставляя значения показателей по достоверности, полноте и своевременности можно определить фактические или прогнозируемые значения показателей по производительности и себестоимости.

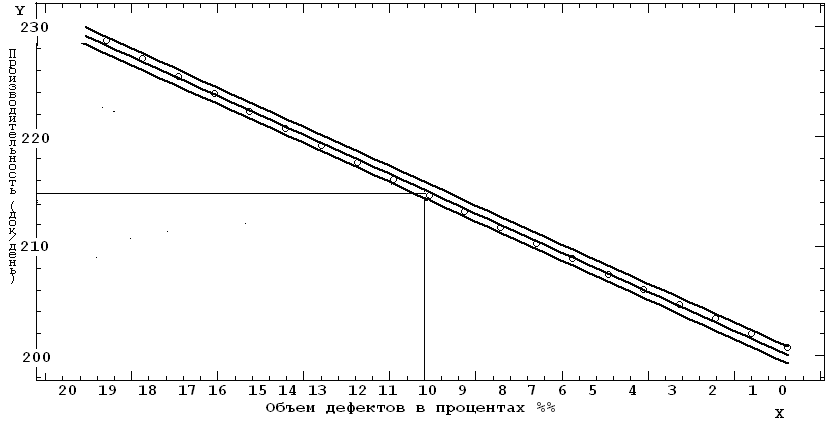
Рис. 4.5. График зависимости производительности ИС от снижения

трудоемкости устранения дефектов обработки

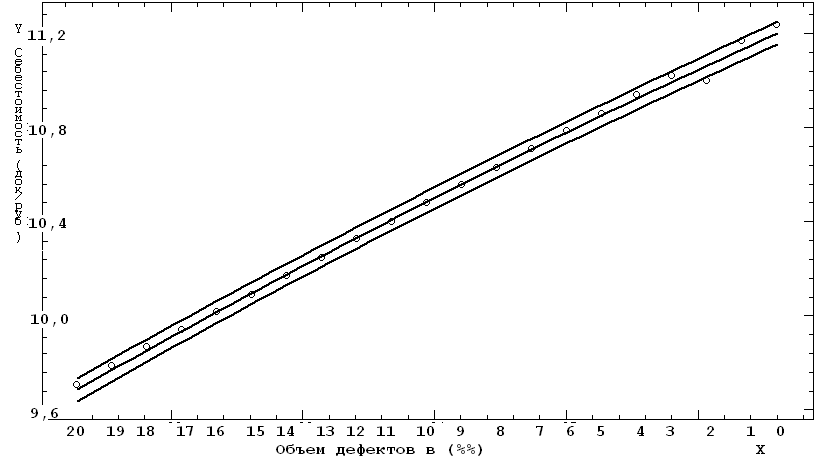
Рис. 4.6. График зависимости себестоимости обработки документов от снижения трудоемкости устранения дефектов обработки

Таблица 4.9

Коэффициенты регрессии по производительности и данные их оценки

Вид (коэффици-ента)	Значение коэффициента регресссии	Стандартная ошибка коэффициента	Уровень значимости нулевой гипотезы (Р-значение)
Нулевой	348,9	27	5,95Е-7
Достоверность	-1,452	271,7	0,9915
Полнота	-0,1119	81,56	0,9941
Своевременность	0,07146	23,47	0,993

Коэффициент множественной корреляции – 0,9993;

Коэффициент детерминации – 0,99859;

Приведенная (несмещенная) оценка коэффициента детерминации - 0,99834;

Стандартная ошибка вычислений – 0,37546;

F – значение статистики Фишера для проверки нулевой гипотезы - 4020;

Уровень значимости (Р - значение) нулевой гипотезы -0,0000;

Гипотеза 1: <Регрессионная модель адекватна экспериментальным данным>.

Таблица 4.10

Коэффициенты регрессии по себестоимости и данные их оценки

Вид (коэф-фициента)	Значение коэффициента регресссии	Стандартная ошибка коэффициента	Уровень значимости нулевой гипотезы (Р-значение)
Нулевой	3,663	0.06802	1.037E-8
Достоверность	0.3924	0.5402	0.5162
Полнота	0.0002067	0.0005942	0.7315
Своевре-менность	-0.02332	0.03202	0.5174

Коэффициент множественной корреляции – 0,99917;

Коэффициент детерминации – 0,99833;

Приведенная (несмещенная) оценка коэффициента детерминации – 0,99804;

Стандартная ошибка вычислений – 0,020831;

F – значение статистики Фишера для проверки нулевой гипотезы - 3392;

Уровень значимости (Р - значение) нулевой гипотезы - 0,0000;

Гипотеза 1: <Регрессионная модель адекватна экспериментальным данным>.

Экспериментальная проверка алгоритма. В целях экспериментального исследования, проверки работоспособности и оценки эффективности алгоритма анализу подвергается программа автоматического восстановления данных, реализующая указанный алгоритм. В качестве экспериментального материала привлечено 20 документов (таблица 4.11). Каждый документ состоит из 7 таблиц. Для проверки программы в документы были внесены ситуационные ошибки (таблица 4.11). Объем и модификации ошибок определялись с учетом необходимости проверки максимального набора вероятных типов ошибок и полного объема функциональных свойств программы.

Таблица 4.11

Ведомость ошибок в документах

№№ пп	Наименование организации (сокращенное)	Код предприятия	Адрес и модификация ошибки
			адрес (строка-графа)	значение показателя
				заменяемое	заменяющее
1	2	3	4	5	6
1	Казанский	144000	170200-1	50	51
2	Калининградский	144003	173700-14	51	58
3	Кременчугский	144008	173400-11	406	552
4	Красноярский	179009	01-1	700	704
5	Липецкий	179010	180100-10	451	2051
6	Магнитогорский	179011	173400-кс 180100-10	815 800	825 890
7	Московский	334000	051100-13	0	50
8	Орловский	334010	020200-12	20	25
9	Одинцовский	334011	01-14	59	50
10	Павловский	391010	180100-15	6599	6590
11	Пензенский	391011	180100-13	0	20
12	Саратовский	391023	01-9	0	25
13	Саранский	490001	120200-8	0	10
14	Северный	490005	120200-11	136	150
15	Таганрогский	490009	120700-11	21	73
16	Тульский	491003	121100-4	92	95
17	Тюменский	491009	120800-10	112	122
18	Тагильский	491012	120800-12	0	10
19	Угличский	493019	050100-12 060800-12	76 88	88 76
20	Самарский	494023	-	Без ошибок

С целью получения данных для проведения сравнительного анализа и оценки эффективности рассматриваемой программы экспериментальная обработка осуществляется по двум вариантам. По первому варианту входной контроль отчетов выполняется средствами системы подготовки данных (СПД) с подключением программы автоматического восстановления достоверности значений показателей. Затем указанные отчеты контролируются по второму варианту – только средствами СПД, то есть с отключением рассматриваемой программы. Как по первому, так и по второму вариантам должны быть получены соответствующие протоколы ввода и диагностики ошибок во входных документах (распечатка принтера).

Последующий анализ протоколов ввода показал следующее. Одиночные ошибки автоматически обнаруживаются, вычисляются достоверные значения, затем последние заменяют ошибочные значения и оператору для контроля правильности работы программы выдаются сообщения типа «В документе ХХХХХ УУ обнаружена ошибка, строка ХХХХХХ-графа ХХ, значение ХХ скорректировано на значение УУУУ (таблица 4.11, позиции 1-5,7-12,14-15,17). По двойным и более ошибкам программа обнаруживала ошибки, однозначно идентифицируя их адреса, и выдавала сообщения типа «В документе ХХХХХ УУ обнаружено более одной ошибки, строка ХХХХХХ, содержит ошибку, строка ХХХХХХ, графа ХХ содержит ошибку» (таблица 4.11, позиция 18). Ошибочное значение определяется путем взятия пересечения номеров соответствующих строк и (или) граф. При условии случайной механической перестановки значений показателей по строкам и отсутствия нарушения контрольной суммы по графе (в строке 01) было выдано сообщение типа «В документе ХХХХХ УУ обнаружено более одной ошибки, строка ХХХХХ содержит ошибку, строка ХХХХХХ содержит ошибку, графа ХХ содержит ошибку» (таблица 4.11, позиция 19). Точно также идентифицируется «перестановка» значений показателей по графам. В процессе экспериментального исследования оператором подготовки данных была внесена непреднамеренная ошибка в отчет предприятия «Магнитогорский». В строке 180100, графа 10, в значении показателя 890 цифра 9 была ошибочно заменена на цифру 0, то есть, получено ошибочное значение 800. Поскольку в этот отчет ранее была внесена ситуационная ошибка, то программа выдала сообщение о двух ошибках и их адресах (таблица 4.11, позиция 6). В отчет предприятия «Самарский» ситуационные ошибки не вносили, при подготовке данных ошибок также не было, поэтому программа идентифицировала указанный отчет как безошибочный.

4.3. Оценка и анализ адекватности моделей и результатов экспериментов

По результатам обработки ЭВМ были получены данные, содержащие статистические оценки, в частности, среднее выборочное, среднее квадратичное отклонение, мода, медиана, коэффициенты вариации, ассиметрии, эксцесса, гистограммы классов дефектов по параметрам времени и стоимости, согласия эмпирических распределений дефектов с теоретическими и др. По каждой КДРД (таблицы 4.1-4.6) приведены выборочные оценки. На основе этих, а также в последующем полученных данных, были проведены необходимые расчеты (приложение 4) с целью заполнения «Карты оценки и анализа качества» (таблица 4.14) и выполнения анализа по соответствующей методике [122].

Оценка параметров ИС обычно проводится при уровне значимости 0,05, так как с учетом содержания данной задачи этого достаточно. Таблицы показывают, что полученные средние значения по указанному уровню достаточно хорошо укладываются в границы доверительных интервалов. В результате обработки распечатываются также гистограммы распределения частот дефектов, как по времени, так и по стоимости. Проверка эмпирических распределений показала, что случайные величины подчиняются нормальному закону распределения.

Для определения функциональной зависимости между временем и стоимостью обнаруженных и исправленных дефектов использована программа канонического анализа. В результате обработки, в частности, установлено, что между указанными переменными существует сравнительно тесная зависимость. Так, коэффициент канонической корреляции равен 0,99999, коэффициент множественной корреляции равен 0,99998. Вариации значений указанных коэффициентов относительно массивов находится в границах 5-го знака после запятой. Данное условие, в частности, свидетельствует о том, что в последующих измерениях и оценки качества обработки УБ можно не регистрировать стоимость дефектов, так как полученное по соответствующей программе соотношение «время (мин.)»: «стоимость (коп.)» равно 1:13. Однако это положение правомерно до изменения условий эксплуатации ИС, например, обновления комплекса технических средств, изменения оплаты труда работников и др.

Для проверки адекватности регрессионной модели обратимся к содержанию полученных в результате экспериментальной обработки оценок (таблицы 4.9, 4.10). Проверка регрессионных моделей показала в целом по гипотезе № 1 их адекватность экспериментальным данным. Относительно коэффициентов множественной корреляции, коэффициентов детерминации, критериев Фишера, уровней значимости нулевой гипотезы и других оценок, можно принять, что качество линейного прогноза хорошее.

Более четкое заключение можно дать на основе анализа остатков. В результате обработки получена информация по анализу остатков. Она приведена в таблицах 4.12 и 4.13. Графики зависимости величины нормированного остатка от величины процента приведены на рис. 4.7 и 4.8.

Значения производительности и себестоимости и анализ параметров показывает, что значения остатков незначительны как в абсолютном, так и относительном измерениях. Визуальную проверку адекватности модели удобнее всего выполнить по графикам зависимости величин нормированных остатков от величин процентов снижения дефектов соответственно по производительности и себестоимости (рис. 4.7, 4.8). К обработке и построению графиков целесообразно привлечь нормированные остатки, указанные в графе «Остаток в единицах стандартного отклонения» соответственно таблиц 4.12 и 4.13.

По полученным графикам можно установить следующее. График зависимости величины нормированного остатка от величины процента снижения дефектов по стоимости (рис. 4.8) показывает отсутствие четко выраженного криволинейного тренда. Наблюдается случайный разброс, свидетельствующий о том, что модель

Таблица 4.12

Данные анализа остатков регрессии по производительности

Зна-че-ние %	Номинальное значение производительности (Yэксп.)	Значение прогноза производительности (Yрегр.)	Остаток (Yэксп - Yрегр.)	Остаток в единицах стандартного отклонения	Стандартная ошибка среднего значения (d/Yрегр)	95% до-верительный интервал (iYрегр.)
0	200.8	200.1	0.661	1.91	0.3756	0.7832
1	202.1	201.6	0.4351	1.257	0.3717	0.775
2	203.4	203.1	0.2691	0.7774	0.3681	0.7675
3	204.7	204.6	0.1332	0.3847	0.3649	0.7609
4	206.1	206.1	-.002805	-0.008104	0.3621	0.7551
5	207.4	207.6	-0.1088	-0.3142	0.3598	0.7501
6	208.8	209	-0.2047	-0.5914	0.3578	0.7461
7	210.3	210.5	-0.2707	-0.782	0.3563	0.7429
8	211.7	212	-0.3266	-0.9436	0.3552	0.7406
9	213.1	213.5	-0.3626	-1.048	0.3545	0.7392
10	214.6	215	-0.3786	-1.094	0.3543	0.7388
11	216.1	216.5	-0.3745	-1.082	0.3545	0.7392
12	217.6	218	-0.3505	-1.013	0.3552	0.7406
13	219.2	219.4	-0.2865	-0.8275	0.3563	0.7429
14	220.7	220.9	-0.2224	-0.6425	0.3578	0.7461
15	222.3	222.4	-0.1284	-0.3709	0.3598	0.7501
16	223.9	223.9	-0.01434	-0.04142	0.3621	0.7551
17	225.5	225.4	0.1197	0.3458	0.3649	0.7609
18	227.2	226.9	0.2837	0.8197	0.3681	0.7675
19	228.8	228.4	0.4478	1.294	0.3717	0.775
20	230.5	229.8	0.6818	1.97	0.3756	0.7832

Таблица 4.13

Данные анализа остатков регрессии по себестоимости

Зна-че-ние %	Номина-льное значение про-изводительности (Yэксп.)	Значение прогноза производительности (Yрегр.)	Остаток (Yэксп - Yрегр.)	Остаток в единицах стандартного отклонения	Стандартная ошибка среднего значения (d/Yрегр)	95% до-верительный интервал (iYрегр.)
1	2	3	4	5	6	7
0	11.24	11.25	-0.005596	-1.762	0.003446	0.007186
1	11.17	11.17	0.0007875	0.2479	0.00341	0.00711
2	11.09	11.09	-0.002168	-0.6827	0.003377	0.007042
3	11.02	11.02	0.00435	1.37	0.003348	0.006981
4	10.94	10.94	0.001064	0.3349	0.003322	0.006928
5	10.86	10.86	-0.002223	-0.6998	0.003301	0.006882
6	10.79	10.79	0.004295	1.352	0.003283	0.006845
7	10.71	10.71	0.0002629	0.08279	0.003269	0.006816
8	10.63	10.63	-0.002277	-0.717	0.003259	0.006795
9	10.56	10.56	0.004478	1.41	0.003253	0.006782
10	10.48	10.48	0.0009548	0.3006	0.003251	0.006778
11	10.4	10.4	-0.002331	-0.734	0.003253	0.006782
12	10.33	10.33	0.004383	1.38	0.003259	0.006795
13	10.25	10.25	0.0009007	0.2836	0.003269	0.006816
14	10.17	10.17	-0.002385	-0.7511	0.003283	0.006845
15	10.09	10.1	-0.005671	-1.786	0.003301	0.006882
16	10.02	10.02	0.0008466	0.2666	0.003322	0.006928
17	9.94	9.942	-0.002439	-0.7681	0.003348	0.006981
18	9.87	9.866	0.004274	1.346	0.003377	0.007042
19	9.79	9.789	0.0009882	0.3112	0.00341	0.00711
20	9.71	9.712	-0.002494	-0.7851	0.003446	0.007186

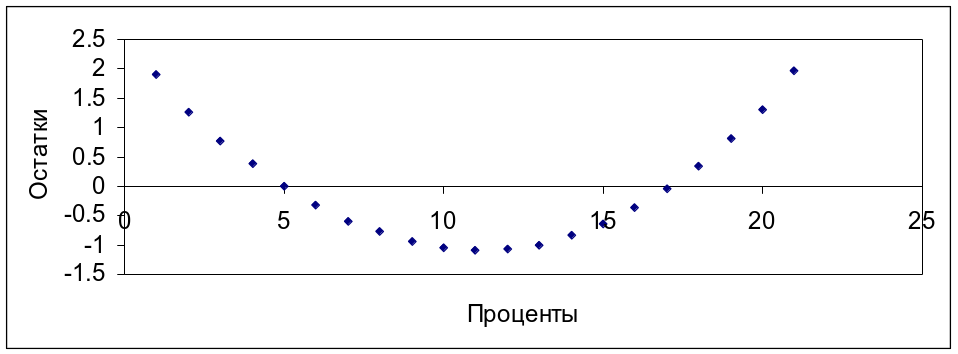
Рис. 4.7. График зависимости величины нормированного остатка от величины процента снижения дефектов по времени

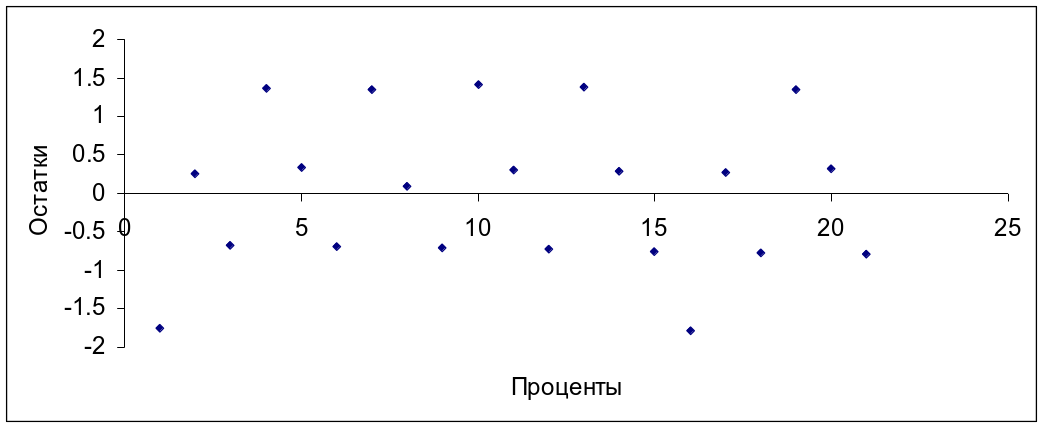
Рис. 4.8. График зависимости величины нормированного остатка от величины процента снижения дефектов по стоимости

едва ли можно или целесообразно улучшить. Сравнительная смещённость, например, распределения настолько мала (близость к оси), что не имеет принципиального значения относительно номинальных величин прогнозируемой переменной по себестоимости (таблица 4.13). Вместе с тем график зависимости величины нормированного остатка от величины процента снижения дефектов по времени (рис. 4.7) показывает незначительный криволинейный тренд. В общем случае это может означать, что в модели вероятно не учтен какой-либо фактор, либо допущены некоторые ошибки в расчетах. Первое условие маловероятно (пропуск фактора), так как кластер-анализ показал только три фактора, с одной стороны, и это условие не подтверждается распределением нормированных остатков по стоимости (рис. 4.8.). Более всего вероятным в данном случае является второе условие. Кроме того, следует учитывать вероятность действия в принципе обоих вышеуказанных и других условий, как это принято в модели регрессии (формула 3.35). Вместе с тем, график показывает, что смещённость распределения остатков относительно оси настолько мала, что в практическом отношении эта смещённость не имеет принципиального значения относительно номинальных величин прогнозируемой переменной по производительности (таблица 4.12, графа «Остаток»). С учетом вышеизложенного можно констатировать, что полученные модели адекватны экспериментальным данным.