Файл: Точек, являющихся образом множества объектов, и множества линий.docx

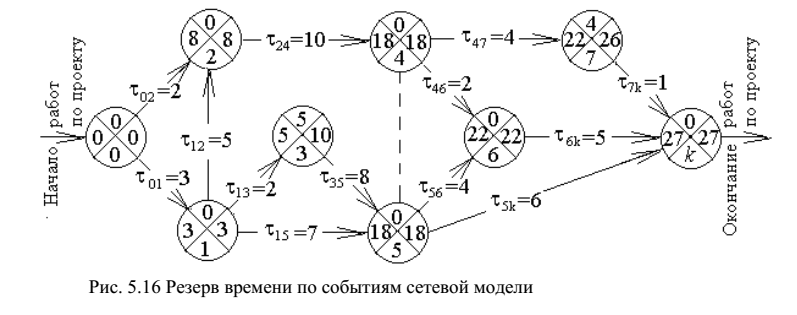
На рисунке представлены результаты вычислений поздних моментов событий:

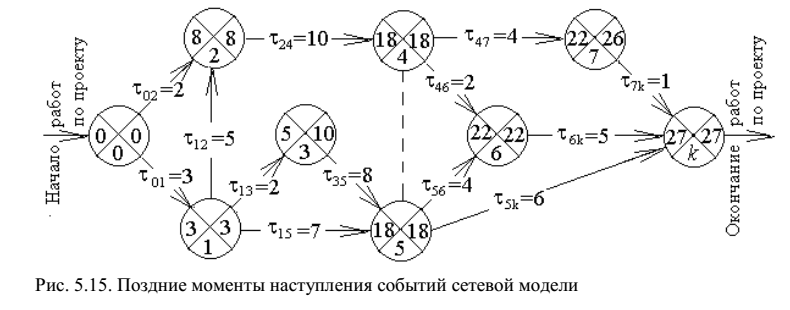
Расчеты резерва времени каждого события

Для решения задачи по каждой вершине i рассчитывается ее резерв времени 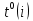по формуле :

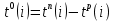r	0	1	2	3	4	5	6	7	8
i	0	1	2	3	4	5	6	7	8
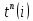	0	3	8	10	18	18	22	26	27
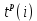	0	3	8	5	18	18	22	22	27
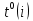	0	0	0	5	0	0	0	4	0

---

На рисунке приведены результаты вычислений резервов времени на события:

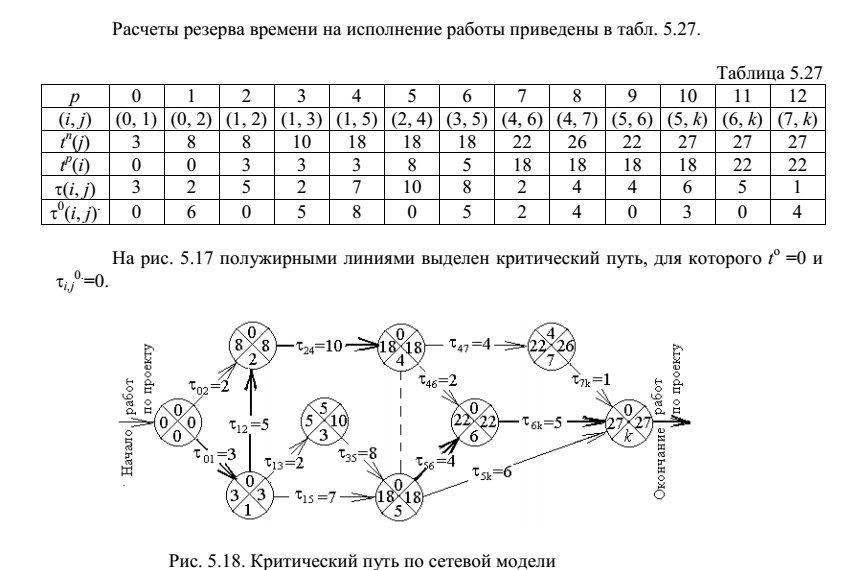
Расчеты резерва времени на исполнение работы

Для решения задачи по каждой дуге (i, j) рассчитывается резерв времени 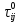на соответствующую работу по формуле :

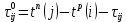r	0	1	2	3	4	5	6	7	8	9	10	11	12
(i,j)	(0,1)	(0,2)	(1,2)	(1,3)	(1,5)	(2,4)	(3,5)	(4,6)	(4,7)	(5,6)	(5,k)	(6,k)	(7,k)
	3	8	8	10	18	18	18	22	26	22	27	27	27
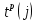	0	0	3	3	3	8	5	18	18	18	18	22	22
	3	2	5	2	7	10	8	2	4	4	6	5	1
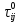	0	6	0	5	8	0	5	2	4	0	3	0	4

---

На рисунке полужирными линиями выделен критический путь, для которого 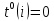и :


Анализ результатов вычислений по сетевой модели показывает:

• 
  события 1, 2, 4, 5, 6 не имеют резерва времени на событие, то есть они принадлежат критическому пути,
  
• 
  работы (0, 1), (1, 2), (2, 4), (5, 6), (6, k) не имеют резерва времени на работу, то есть они также принадлежат критическому пути,
  
• 
  события 3 и 7 имеют резерв времени, что позволяет ослабить внимание на исполнение работ τ₁₃, τ₃₅, τ₄₇, τ_7k или уменьшить затраты ресурсов на их исполнение,
  
• 
  работы (0, 2), (1,5), (4, 6), (5, k) имеют резерв времени, что позволяет продлить исполнение этих работ или также уменьшить затраты ресурсов.
  

---

4. Операции на графах

Включают одну унарную операцию и несколько бинарных: объединение, пересечение, разность, композицию.

К унарным операциям относится операция дополнения графа : если есть граф G =<X, R>, то его дополнение есть ¬G=<X, ¬R>, где ¬R ={ 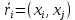} - дополнение отношения R (знак  - дополнение множества отношений, знак 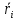– отрицание отношения).

Для дополнения графа матрица смежности вычисляется по правилу:

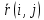=1, если r(i,j)=0;

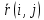=0, если r(i,j)=1.

Ниже приведен граф G и его дополнение:



При исполнении операций над двумя графами G₁=<X₁, R₁> и G₂=<X₂, R₂> следует обращать внимание на наличие общих элементов для вершин и/или линий. Это позволяет выделить три конструктивных объекта:

1. 
   вершины и линии двух графов не имеют общих элементов;
   
2. 
   вершины двух графов имеют общие элементы, а линии - нет;
   
3. 
   вершины и линии имеют общие элементы.
   

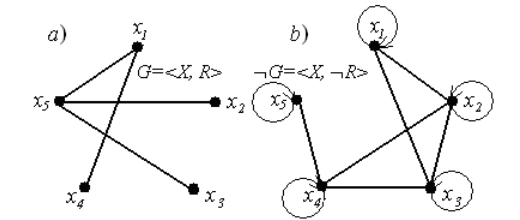
В качестве примера для иллюстрации операций над графами зададимся тремя графами, которые демонстрируют три рассмотренных конструктивных типа:

а) у графов нет общих элементов:



b) у графов есть общие вершины:

---

с) у графов есть общие вершины и линии:



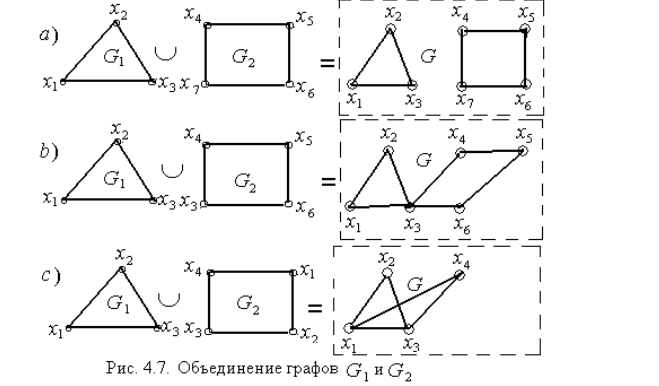
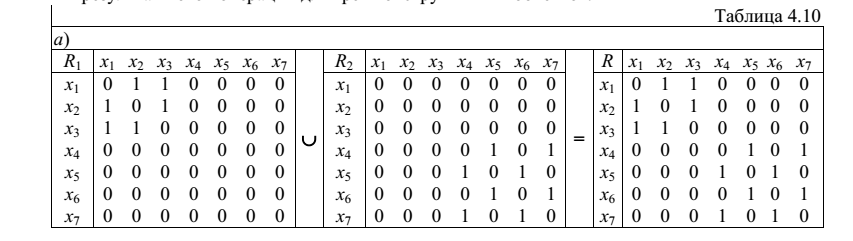
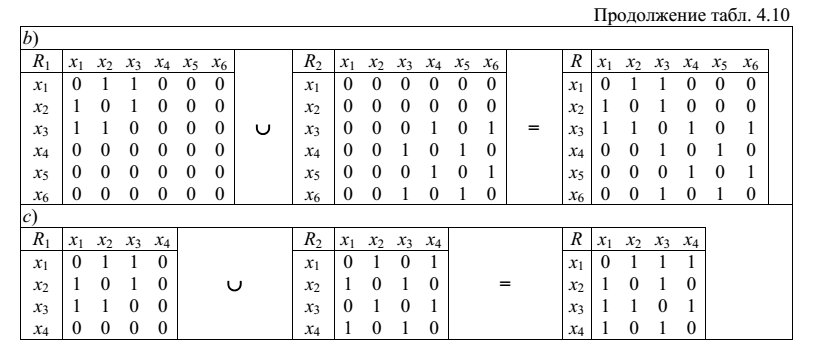
Объединение графов

Если есть графы G₁=<X₁, R₁> и G₂=<X₂, R₂>, то их объединение есть граф G=G₁∪G₂, для которого X=X₁∪X₂ и R=R₁∪R₂.

Для вычисления матрицы смежности графа G следует выполнить объединение матриц смежности графов G₁ и G₂:

1. 
   матрицы смежности исходных графов выравнивают по числу строк и столбцов, при этом недостающие строки и столбцы заполняют нулями;
   
2. 
   значение элементов матрицы смежности результирующего графа вычисляют по формуле: r(i, j)=r₁(i, j) ∨ r₂(i, j).
   

Для приведенных примеров вычисления для матриц смежности, а также графические результаты выполнения операции приведены ниже:

а)





b)



c)

---