Файл: Точек, являющихся образом множества объектов, и множества линий.docx

х₂
х₅

6. 
   для вершины х₅ выбираем первую из списка смежную вершину – это х₁. Она уже есть в остове, однако ребро (х₅,х₁) отсутствует. Добавляем его в остов как обратное ребро (имеет пунктирный формат):
   

х₁


х₂
х₅

7. 
   следующая для вершины х₅ смежная вершина – х₂. Она тоже присутствует в остове также, как и ребро (х₂,х₅). Остов не меняется;
   
8. 
   следующая для вершины х₅ смежная вершина – х₃. Ее в остове нет, добавляем и соединяем с х₅ прямым ребром:
   

х₁


х₂


х₅
х₃

9. 
   выбираем первую смежную вершину для вершины х₃ – это х₂. Поскольку вершина уже есть, а ребра (х₂,х₃) нет, добавляем его как обратное ребро:
   

х₁


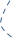
х₂


х₅
х₃

10. 
    для вершины х₃ выбираем следующую смежную вершину – х₄. Поскольку ее нет в остове, добавляем и строим новое прямое ребро:
    

х₁


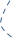
х₂

---

х₅
х₃


х₄

11. 
    для вершины х₄ ищем первую смежную вершину – это х₂. Она уже есть в остове, добавляем обратное ребро (х₄,х₂):
    

х₁


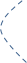
х₂


х₅
х₃


х₄

12. 
    следующая смежная вершина для х₄ – х₃. В остове присутствует и она, и ребро (х₃,х₄);
    
13. 
    следующая смежная вершина для х₄ – х₅. Она в остове есть, а ребра (х₄,х₅) нет, поэтому добавляем его как обратное:
    

х₁


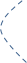
х₂


х₅
х₃


х₄

14. 
    поскольку список смежных вершин для х₄ исчерпан, возвращаемся к вершине х₃: для нее очередная (и последняя в списке) смежная вершина – х₅. В остове есть как сама вершина, так и ребро (х₃,х₅). Остов не меняется, возвращаемся к вершине х₅. Для этой вершины выбираем очередную (и последнюю) смежную вершину х₄ – в остове есть и сама вершина, и ребро (х₄,х₅), поэтому остов не меняется;
    
15. 
    выбираем очередную смежную вершину для вершины х₂ – это х₄. Поскольку в остове есть и она, и ребро (х₂,х₄), остов не меняется. Аналогично поступаем и с последней смежной вершиной для х₂ – х₃;
    
16. 
    возвращаемся к вершине х₁: последняя смежная для нее вершина – х₅: в остове есть и эта вершина и ребро (х₁,х₅), поэтому построение остова заканчиваем. Его окончательный вариант:
    

---

х₁


х₂


х₅
х₃


х₄

Обратные ребра формируют циклы в графе: это (х₁,х₅), (х₂,х₃), (х₂,х₄), (х₅,х₄). Их удаление даст граф без циклов:

х₁


х₂


х₅
х₃


х₄

---

2.3. Плотность графа

Наибольшее число вершин подграфа G_i=<X_i;R_i> связного графа G=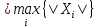, R>, где X_i ⊆ X и R_i ⊆ R, между всеми вершинами которого попарно есть отношение смежности, называют плотностью графа и обозначают ρ(G) . Таких полных подграфов в связном графе может быть несколько. Поэтому необходимо проверить отношение смежности каждой пары вершин каждого полного подграфа и выбрать подмножество X_i, содержащее наибольшее число вершин.

Для графа G, изображенного на рисунке,



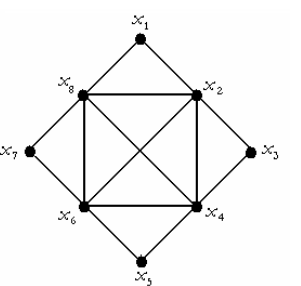
полные подграфы представлены множествами вершин: X₁={x₂, x₃, x₄}, X₂={x₄, x₅, x₆}, X₃={x₆, x₇, x₈}, X₄={x₁, x₂, x₈}, X₅={x₂, x₄, x₆, x₈}. Следовательно, ρ(G)=max{|X₁|, |X₂|, |X₃|, |X₄|, |X₅|}=4.
Поиск плотности графа

Для этого необходимо вычислить матрицу достижимости Q = IR и выполнить неоднократно перестановку строк и столбцов (не более n! раз) так, чтобы найти клетки главной диагонали, содержащие наибольшее число «1». Такая клетка есть образ полного подграфа, а «1» в строке или столбце клетки указывает на имя вершины полного подграфа.

Пример: определить плотность графа на приведенном выше рисунке.

Решение задачи:

1. 
   составим для заданного графа матрицу смежности R и матрицу достижимости Q:
   

R	x1	x2	x3	x4	x5	x6	x7	x8		Q	x1	x2	x3	x4	x5	x6	x7	x8
x1	0	1	0	0	0	0	0	1		x1	1	1	0	0	0	0	0	1
x2	1	0	1	1	0	1	0	1		x2	1	1	1	1	0	1	0	1
x3	0	1	0	1	0	0	0	0		x3	0	1	1	1	0	0	0	0
x4	0	1	1	0	1	1	0	1		x4	0	1	1	1	1	1	0	1
x5	0	0	0	1	0	1	0	0		x5	0	0	0	1	1	1	0	0
x6	0	1	0	1	1	0	1	1		x6	0	1	0	1	1	1	1	1
x7	0	0	0	0	0	1	0	1		x7	0	0	0	0	0	1	1	1
x8	1	1	0	1	0	1	1	0		x8	1	1	0	1	0	1	1	1

2. 
   проанализируем матрицу достижимости Q – она содержит 3 пересекающиеся клетки, заполненные единицами (выделены ниже в таблице):
   

Q	x1	x2	x3	x4	x5	x6	x7	x8
x1	1	1	0	0	0	0	0	1
x2	1	1	1	1	0	1	0	1
x3	0	1	1	1	0	0	0	0
x4	0	1	1	1	1	1	0	1
x5	0	0	0	1	1	1	0	0
x6	0	1	0	1	1	1	1	1
x7	0	0	0	0	0	1	1	1
x8	1	1	0	1	0	1	1	1

Видно, что эти клетки «опираются» на множества вершин Х₁={x₂, x₃, x₄}, Х₂={x₄, x₅, x₆} и Х₃={x₆, x₇, x₈}, которые упоминались ранее. Отсутствие клетки, соответствующей множеству вершин X₄={x₁, x₂, x₈} восполнимо: для этого надо сделать перестановки нужных одноименных столбцов и строк матрицы достижимости:

Q	x1	x2	x8	x3	x4	x5	x6	x7
x1	1	1	1	0	0	0	0	0
x2	1	1	1	1	1	0	1	0
x8	1	1	1	0	1	0	1	1
x3	0	1	0	1	1	0	0	0
x4	0	1	1	1	1	1	1	0
x5	0	0	0	0	1	1	1	0
x6	0	1	1	0	1	1	1	1
x7	0	0	1	0	0	0	1	1

3. 
   для поиска клетки с наибольшим числом вершин выполним одновременные перестановки одноименных столбцов и строк (число перестановок не более 8!):
   

Q	x3	x2	x4	x6	x8	x7	x1	x5
x3	1	1	1	0	0	0	0	0
x2	1	1	1	1	1	0	1	0
x4	1	1	1	1	1	0	0	1
x6	0	1	1	1	1	1	0	1
x8	0	1	1	1	1	1	1	0
x7	0	0	0	1	1	1	0	0
x1	0	1	0	0	1	0	1	0
x5	0	0	1	1	0	0	0	1

Видно, что на главной диагонали выделена одна клетка, содержащая четыре вершины {x₂, x₄, x₆, x₈}. Следовательно, ρ(G)=4.

1   2   3   4   5   6   7   8   9   ...   17

---

2.4 Хроматическое число графа

Если удается множество вершин связного графа G = <X, R> разбить на подмножества попарно несмежных вершин, то каждому подмножеству X_iможно выделить один цвет. Наименьшее число таких подмножеств (или цветов), при котором никакие две смежные вершины не окрашены в один цвет, называют хроматическим числом графа и обозначают γ(G).

Существуют следующие оценки хроматического числа:

1. 
   хроматическое число полного n–вершинного графа равно n,
   
2. 
   пустого графа – 1,
   
3. 
   графа с циклом четной длины – 2,
   
4. 
   графа с циклом нечетной длины – 3,
   
5. 
   графа типа дерево – 2,
   
6. 
   для оценки хроматического числа графа, имеющего сложную структуру и содержащего циклы четной и нечетной длины, может быть рекомендована формула: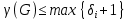 , где 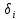– степень i-й вершины.
   

Пример: на рисунке дан раскрашенный граф, степени вершин которого приведены в таблице. Определить хроматическое число.

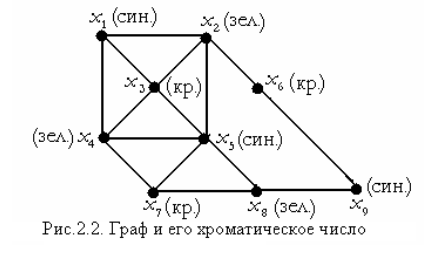
Х	х1	х2	х3	х4	х5	х6	х7	х8	х9
i	3	4	4	4	5	2	3	3	2

Анализ графа показывает, что он содержит циклы четной и нечетной длины. Например, (х₁,х₂), (х₂,х₃), (х₃,х₁) – длина 3; (х₁,х₂), (х₂,х₅), (х₅,х₄), (х₄,х₁) – длина 4.

Для определения хроматического числа воспользуемся формулой:

---