Файл: Точек, являющихся образом множества объектов, и множества линий.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 25.10.2023

Просмотров: 243

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Оглавление

1. Граф и его характеристики

1.2. Описание графа

2. Числа графа и их определение

2.2. Цикломатическое число графа

2.3. Плотность графа

2.4 Хроматическое число графа

3. Некоторые алгоритмы на графах

3.1. Поиск покрывающего остова (обход вершин графа)

3.2. Поиск остова минимального веса

3.3. Поиск кратчайших путей в графе

3.4. Поиск критического пути в графе

4. Операции на графах





  1. после расчета раннего времени наступления события 2 можно рассчитать раннее время наступления события 4:




r
i
j=h(i)


6
2
4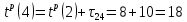





  1. после определения ранних моментов наступления событий 4 и 5, связанных фиктивной работой, можно уточнить итоговые ранние времена наступления обоих событий:




r
i
j=h(i)




7
4
5
ожидание: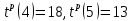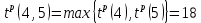



5
4


Поскольку вершина 4 имеет максимальное значение раннего времени наступления события, именно это значение, равное 18, присваивается вершине 5 (в таблице это действие не отражено);

  1. на данном этапе можно рассчитать ранние моменты наступления событий для вершин 7 (имеет только одну входящую дугу) и 6 (имеет две входящие дуги):




r
i
j=h(i)


8
4
7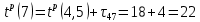




r
i
j=h(i)




9
4
6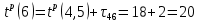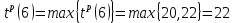




10
5
6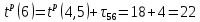





  1. теперь определены все моменты наступления ранних событий, чтобы решить аналогичную задачу для вершины k, имеющей три входящие дуги:



r
i
j=h(i)




11
5
k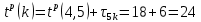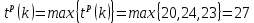




12
6
k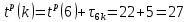


13
7
k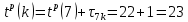



На рисунке представлены результаты вычислений ранних моментов событий:



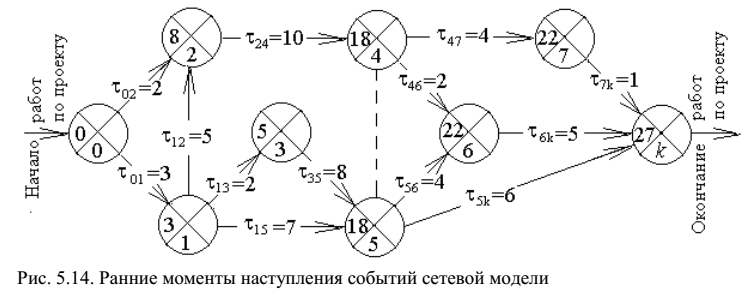
Расчет поздних моментов наступления каждого события


Исходные данные для этого расчета берутся из результатов решения предыдущей задачи, однако сеть просматривается в направлении от своего стока к истоку, т.е. от вершины k к вершине 0.

По аналогии с предыдущей задачей выделим группы вершин в зависимости от числа исходящих дуг и в соответствии с наличием ожидания:

  1. по одной исходящей дуге имеют вершины – 7, 6, 3, 2,

  2. вершины с несколькими исходящими дугами – 5, 4, 1, 0,

  3. вершины, связанные фиктивной работой, по-прежнему – 4 и 5.

В соответствии со структурой исходной сети определим последовательность расчетов:

  1. поскольку известно позднее время вершины k (tп(k) = 27), можно решить аналогичную задачу для вершин 7, 4, образующих переход, а также для вершин 5 и 6 (поскольку вершины 4 и 5 имеют по две исходящие дуги, расчеты для них пока не окончательны, что показано желтым цветом):




r
i
j=h-1(i)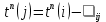


0
k
7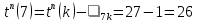


1
7
4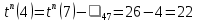


2
k
5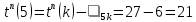


3
k
6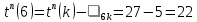





  1. теперь можно определить предварительные (пока без учета ожидания) искомые параметры для вершин 4 и 5:




r
i
j=h-1(i)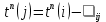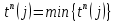




4
6
4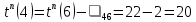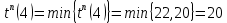




5
5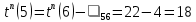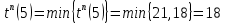







  1. примем во внимание ожидание между вершинами 4 и 5 и определим окончательно поздние времена наступления соответствующих событий:



r
i
j=h-1(i)




6
4
5
ожидание: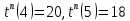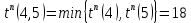



5
4




  1. с вершиной 5 смежны вершины 3 и 1. Определим для них поздние времена наступления событий, причем для вершины 1, имеющей две исходящие дуги, это будет предварительный расчет:




r
i
j=h-1(i)


7
5
3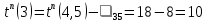


8
5
1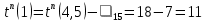





  1. рассчитаем позднее время наступления события для вершины 2 с одной исходящей дугой:




r
i
j=h-1(i)


9
4
2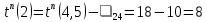





  1. дальнейшие расчеты выполним для вершины 1 с тремя исходящими дугами:




r
i
j=h-1(i)


10
3
1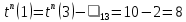





r
i
j=h-1(i)




11
2
1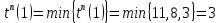







  1. наконец рассчитаем позднее время наступления события для вершины 0:




r
i
j=h-1(i)


12
2
0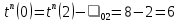





r
i
j=h-1(i)




13
1
0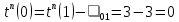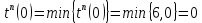



Смотрите также файлы