Файл: Точек, являющихся образом множества объектов, и множества линий.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 234
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2. Такую процедуру повторять пока ни будут просмотрены образы каждой вершины графа до xn включительно.
Так могут быть найдены множества прямых и обратных ребер. Первые формируют скелет дерева (см. рисунок), вторые – выделяют циклы на графе (см. таблицу):


Пример: на рисунке изображен граф, а в таблице – окружение каждой вершины.
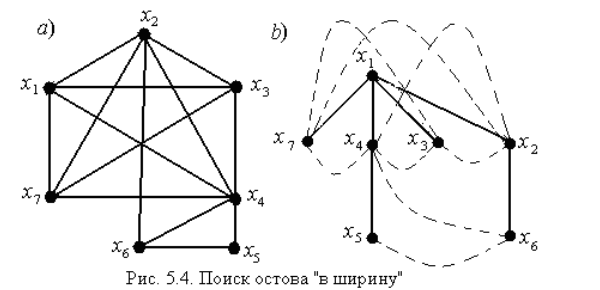
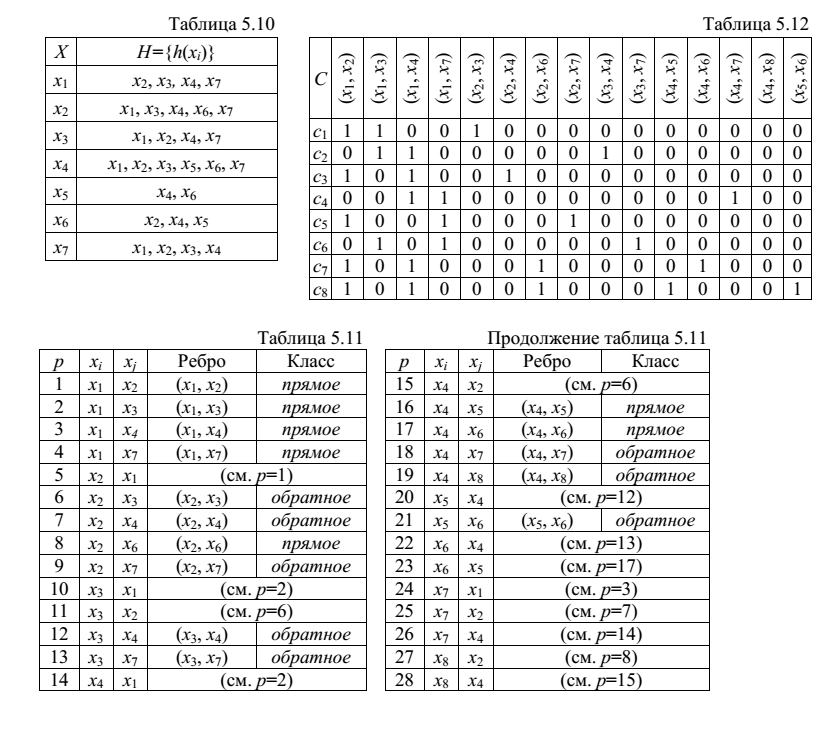
Построить покрывающий остов по алгоритму поиска «в ширину», приняв за начальную вершину x1– корень дерева.
На рисунке изображен покрывающий остов и сплошными линиями обозначены прямые, а пунктирными – обратные ребра.

В таблице показана последовательность выбора смежных вершин xk∈h(xj) согласно списку отображений:

Первые четыре шага описывают формирование фрагмента остова только из окружения вершины x1. Так как все образы x1 и инцидентные им ребра включены во фрагмент остова, то выбираем из очереди для x1 очередную вершину x2. Проверим окружение x2: включены ли вершины, смежные x2 во фрагмент остова? Если вершина не включена во фрагмент остова, то ее и инцидентное ей ребро включить во фрагмент остова. Если вершина включена во фрагмент остова, то инцидентное данной вершине ребро не включать во фрагмент остова. Последнее ребро замыкает цикл на графе, поэтому его включают во множество обратных ребер. Так обнаружено одно прямое ребро (x2, x6) и три обратных ребра (x
2, x3), (x2, x4), (x2, x7). Если все вершины – образы x2 исследованы, то выбираем из очереди вершин, смежных x2, очередную вершину x3. Проверяем окружение x3: включены ли вершины, смежные x3, во фрагмент остова, есть ли прямые и обратные ребра? Цикл повторять пока ни будут просмотрены образы каждой вершины графа до xn включительно. Так найдены множества прямых и обратных ребер. Первые формируют скелет дерева (см. ранний рисунок), вторые – циклы на графе (см. таблицу):

Задача поиска остова дерева имеет свое развитие – поиск остова минимального веса. Решение этой задачи имеет большое значение в проектировании вычислительных сетей, в организации грузоперевозок или ремонтных работ на транспортной сети.
Если есть некоторый фрагмент остова Gi=<Xi, Ri> и среди множества ребер riесть ребро, инцидентное одной из вершин фрагмента хi∈Xiи имеющее наименьший вес l(хi, хj), то включить во фрагмент вторую вершину ребра хjи ребро l(хi, хj). Процедуру продолжать до включения во фрагмент (n–1)-го ребра графа, где n – число вершин графа. Эта идея реализуется двумя алгоритмами – Дейкстры и Краскала.
Алгоритм Дейкстры
Заключается в задании начальной вершины остова x0 и в последовательном определении минимального расстояния до одной из вершин, принадлежащих фрагменту:
шаг 1: выбрать начальную вершину x0,
шаг 2: выбрать ребро наименьшего веса l(х0, хi), инцидентное начальной вершине, и сформировать фрагмент Gi=<Xi, Ri>, включив вторую концевую вершину в подмножество Хi={x0, xi},
шаг 3: выбрать ребро наименьшего веса, инцидентное вершинам фрагмента и не являющееся петлей:
а) если вторая концевая вершина не принадлежит фрагменту, то включить ее и ребро во фрагмент остова Gi=<Xi, Ri>,
b) если вторая концевая вершина принадлежит фрагменту, то исключить ребро из анализа (это ребро формирует цикл на графе),
шаг 4: если все вершины графа вошли во фрагмент остова, то конец, иначе перейти к шагу 3.
Пример: найти минимальные по протяженности маршруты вывоза контейнеров бытового мусора (
xi) района на полигон (x0).
На карте, изображенной на рисунке, контейнеры располагаются в узлах уличной сети xi:
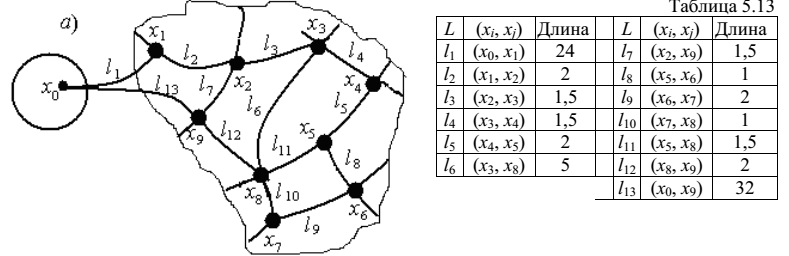
Протяженность участков уличной сети li приведена в условных единицах в таблице:

В таблице приведены результаты поиска минимального остова по шагам итерации:

На рисунке по результатам поиска показан остов минимального веса (его протяженность 36 у.е.):
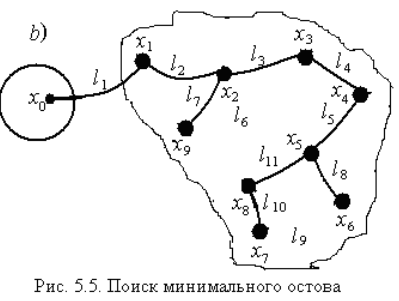
Суммарная протяженность переброски содержимого всех n контейнеров одной автомашиной на полигон и возвращение освобожденных контейнеров обратно равна: Lобщ.=2(nl1+(n–1)l2+l7+(n–3)l3+(n–4)l4+(n–5)l5+l8+(n–7)l11+l10) = 526 у. е.
Алгоритм Краскала
Заключается в частичном упорядочении множества ребер графа li≤lj≤…≤ln, а затем в последовательном их включении в подмножество ребер фрагмента остова ri. При этом инцидентные ребру вершины включаются в подмножество вершин фрагмента. Если две концевые вершины ребра уже принадлежат фрагменту, то ребро не включается во фрагмент остова (это ребро формирует цикл). При последовательном исполнении алгоритма могут формироваться несколько фрагментов, которые на очередном этапе итерации сливаются в единый остов. Вычисления по алгоритму продолжаются пока ни будут включены в подмножество Xiвсе вершины исходного графа:
шаг 1: установить частичный порядок по весу (продолжительности, протяженности, стоимости, трудоемкости и т.п.) ребер графа,
шаг 2: выбрать ребро минимального веса, не являющееся петлей, сформировать фрагмент остова Gi=<Xi, Ri>, а концевые вершины ребра включить в подмножество Хi⊆Х,
шаг 3: выбрать ребро минимального веса, не являющееся петлей и не принадлежащее фрагменту:
а) если фрагменту принадлежит одна вершина ребра, то вторую концевую вершину включить в подмножество Хi, а ребро включить во фрагмент остова Gi=<Xi, Ri>,
b) если ни одна концевая вершина ребра не принадлежит фрагменту остова, то сформировать фрагмент другого остова Gj=<Xj, Rj>,
с) если концевые вершины принадлежат различным остовам Gi=<Xi, Ri> и Gj=<Xj, Rj>, то соединить фрагменты,
d) если ребро формирует цикл, не включать его во фрагмент остова,
шаг 4: если все вершины графа вошли во фрагмент остова, то конец, иначе перейти к шагу 2.
Пример: для района города (см. рисунок) проложить минимальный по протяженности кабель для организации кабельного телевидения:
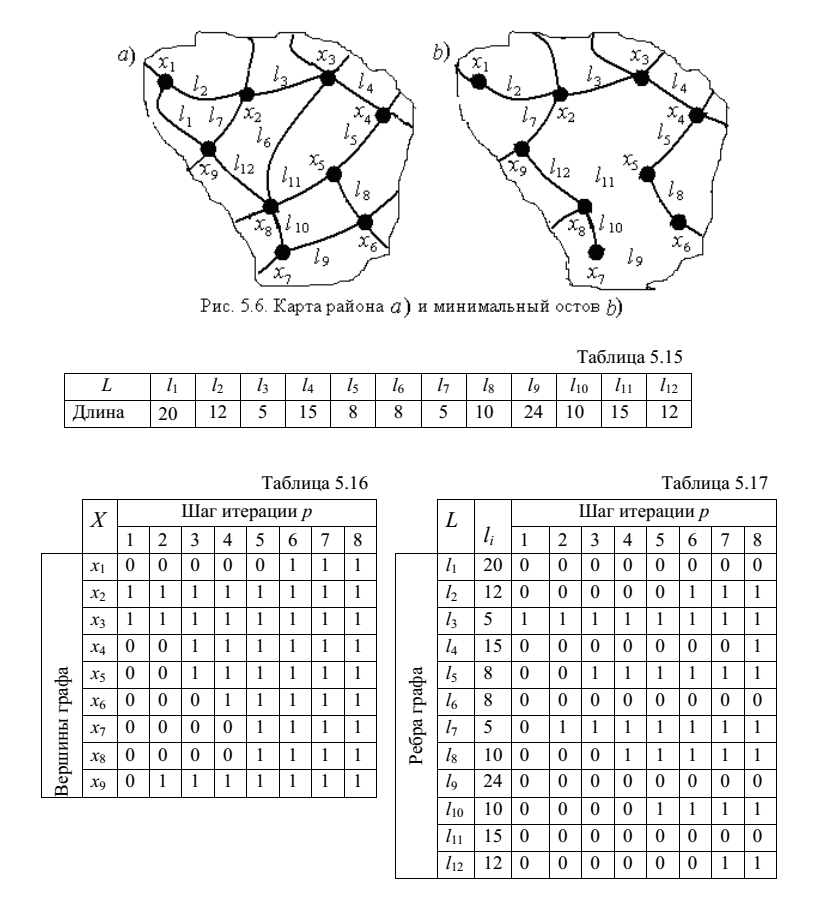
В таблице приведены расстояния между объектами района:
Частичный порядок ребер исходного графа указан в таблице:
Так могут быть найдены множества прямых и обратных ребер. Первые формируют скелет дерева (см. рисунок), вторые – выделяют циклы на графе (см. таблицу):


Пример: на рисунке изображен граф, а в таблице – окружение каждой вершины.


Построить покрывающий остов по алгоритму поиска «в ширину», приняв за начальную вершину x1– корень дерева.
На рисунке изображен покрывающий остов и сплошными линиями обозначены прямые, а пунктирными – обратные ребра.

В таблице показана последовательность выбора смежных вершин xk∈h(xj) согласно списку отображений:

Первые четыре шага описывают формирование фрагмента остова только из окружения вершины x1. Так как все образы x1 и инцидентные им ребра включены во фрагмент остова, то выбираем из очереди для x1 очередную вершину x2. Проверим окружение x2: включены ли вершины, смежные x2 во фрагмент остова? Если вершина не включена во фрагмент остова, то ее и инцидентное ей ребро включить во фрагмент остова. Если вершина включена во фрагмент остова, то инцидентное данной вершине ребро не включать во фрагмент остова. Последнее ребро замыкает цикл на графе, поэтому его включают во множество обратных ребер. Так обнаружено одно прямое ребро (x2, x6) и три обратных ребра (x
2, x3), (x2, x4), (x2, x7). Если все вершины – образы x2 исследованы, то выбираем из очереди вершин, смежных x2, очередную вершину x3. Проверяем окружение x3: включены ли вершины, смежные x3, во фрагмент остова, есть ли прямые и обратные ребра? Цикл повторять пока ни будут просмотрены образы каждой вершины графа до xn включительно. Так найдены множества прямых и обратных ребер. Первые формируют скелет дерева (см. ранний рисунок), вторые – циклы на графе (см. таблицу):

3.2. Поиск остова минимального веса
Задача поиска остова дерева имеет свое развитие – поиск остова минимального веса. Решение этой задачи имеет большое значение в проектировании вычислительных сетей, в организации грузоперевозок или ремонтных работ на транспортной сети.
Если есть некоторый фрагмент остова Gi=<Xi, Ri> и среди множества ребер riесть ребро, инцидентное одной из вершин фрагмента хi∈Xiи имеющее наименьший вес l(хi, хj), то включить во фрагмент вторую вершину ребра хjи ребро l(хi, хj). Процедуру продолжать до включения во фрагмент (n–1)-го ребра графа, где n – число вершин графа. Эта идея реализуется двумя алгоритмами – Дейкстры и Краскала.
Алгоритм Дейкстры
Заключается в задании начальной вершины остова x0 и в последовательном определении минимального расстояния до одной из вершин, принадлежащих фрагменту:
шаг 1: выбрать начальную вершину x0,
шаг 2: выбрать ребро наименьшего веса l(х0, хi), инцидентное начальной вершине, и сформировать фрагмент Gi=<Xi, Ri>, включив вторую концевую вершину в подмножество Хi={x0, xi},
шаг 3: выбрать ребро наименьшего веса, инцидентное вершинам фрагмента и не являющееся петлей:
а) если вторая концевая вершина не принадлежит фрагменту, то включить ее и ребро во фрагмент остова Gi=<Xi, Ri>,
b) если вторая концевая вершина принадлежит фрагменту, то исключить ребро из анализа (это ребро формирует цикл на графе),
шаг 4: если все вершины графа вошли во фрагмент остова, то конец, иначе перейти к шагу 3.
Пример: найти минимальные по протяженности маршруты вывоза контейнеров бытового мусора (
xi) района на полигон (x0).
На карте, изображенной на рисунке, контейнеры располагаются в узлах уличной сети xi:

Протяженность участков уличной сети li приведена в условных единицах в таблице:

В таблице приведены результаты поиска минимального остова по шагам итерации:

На рисунке по результатам поиска показан остов минимального веса (его протяженность 36 у.е.):

Суммарная протяженность переброски содержимого всех n контейнеров одной автомашиной на полигон и возвращение освобожденных контейнеров обратно равна: Lобщ.=2(nl1+(n–1)l2+l7+(n–3)l3+(n–4)l4+(n–5)l5+l8+(n–7)l11+l10) = 526 у. е.
Алгоритм Краскала
Заключается в частичном упорядочении множества ребер графа li≤lj≤…≤ln, а затем в последовательном их включении в подмножество ребер фрагмента остова ri. При этом инцидентные ребру вершины включаются в подмножество вершин фрагмента. Если две концевые вершины ребра уже принадлежат фрагменту, то ребро не включается во фрагмент остова (это ребро формирует цикл). При последовательном исполнении алгоритма могут формироваться несколько фрагментов, которые на очередном этапе итерации сливаются в единый остов. Вычисления по алгоритму продолжаются пока ни будут включены в подмножество Xiвсе вершины исходного графа:
шаг 1: установить частичный порядок по весу (продолжительности, протяженности, стоимости, трудоемкости и т.п.) ребер графа,
шаг 2: выбрать ребро минимального веса, не являющееся петлей, сформировать фрагмент остова Gi=<Xi, Ri>, а концевые вершины ребра включить в подмножество Хi⊆Х,
шаг 3: выбрать ребро минимального веса, не являющееся петлей и не принадлежащее фрагменту:
а) если фрагменту принадлежит одна вершина ребра, то вторую концевую вершину включить в подмножество Хi, а ребро включить во фрагмент остова Gi=<Xi, Ri>,
b) если ни одна концевая вершина ребра не принадлежит фрагменту остова, то сформировать фрагмент другого остова Gj=<Xj, Rj>,
с) если концевые вершины принадлежат различным остовам Gi=<Xi, Ri> и Gj=<Xj, Rj>, то соединить фрагменты,
d) если ребро формирует цикл, не включать его во фрагмент остова,
шаг 4: если все вершины графа вошли во фрагмент остова, то конец, иначе перейти к шагу 2.
Пример: для района города (см. рисунок) проложить минимальный по протяженности кабель для организации кабельного телевидения:

В таблице приведены расстояния между объектами района:
| L | l1 | l2 | l3 | l4 | l5 | l6 | l7 | l8 | l9 | l10 | l11 | l12 |
| Вершины | х1,x9 | x1,x2 | x2,x3 | x3,x4 | x4,x5 | x3,x8 | x2,x9 | x5,x6 | x6,x7 | x7,x8 | x5,x8 | x8,x9 |
| Длина | 20 | 12 | 5 | 15 | 8 | 8 | 5 | 10 | 24 | 10 | 15 | 12 |
Частичный порядок ребер исходного графа указан в таблице:
| L | l3 | l7 | l5 | l6 | l8 | l10 | l2 | l12 | l4 | l11 | l1 | l9 |
| Вершины | х2,x3 | x2,x9 | x4,x5 | x3,x8 | x5,x6 | x7,x8 | x1,x2 | x8,x9 | x3,x4 | x5,x8 | x1,x9 | x6,x7 |
| Длина | 5 | 5 | 8 | 8 | 10 | 10 | 12 | 12 | 15 | 15 | 20 | 24 |