Файл: Точек, являющихся образом множества объектов, и множества линий.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 25.10.2023

Просмотров: 240

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Оглавление

1. Граф и его характеристики

1.2. Описание графа

2. Числа графа и их определение

2.2. Цикломатическое число графа

2.3. Плотность графа

2.4 Хроматическое число графа

3. Некоторые алгоритмы на графах

3.1. Поиск покрывающего остова (обход вершин графа)

3.2. Поиск остова минимального веса

3.3. Поиск кратчайших путей в графе

3.4. Поиск критического пути в графе

4. Операции на графах

. Следовательно, число красок должно быть не больше 6. Анализ графа показал, что достаточно трех красок: красной, синей и зеленой, что удовлетворяет условиям оценки хроматического числа.
Поиск хроматического числа графа

Существует алгоритм поиска хроматического числа графа на основе плотности графа :

  1. если   3, то хроматическое число по значению совпадает с плотностью;

  2. если  < 3, то оценка хроматического числа делается по числу ребер в цикле:

  • для циклов с четным числом ребер  =2;

  • для циклов с нечетным числом ребер  = 3;

  • если в графе есть циклы того и иного вида, то  лежит в пределах от 3 до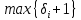 , где δi – степень i-той вершины графа.


Пример: на рисунке дан граф G. Определить его хроматическое число.



Определим число красок по предложенному алгоритму:

  1. ранее была рассчитана плотность этого графа (см. раздел 2.3) -  = 4,

  2. используем это значение для определения хроматического числа: поскольку  > 3, значение хроматического числа совпадает с плотностью, т.е. γ(G) = 4.

Возможное разбиение множества вершин на подмножества: {x1,x6}, {x2,x5}, {x3,x8},{x4,x7}.

На рисунке показано распределение красок между вершинами:


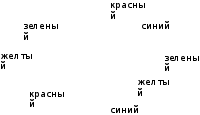
Еще один алгоритм расчета хроматического числа, использующий степени вершин:

  1. Вычислить степени вершин. Принять k= 1.

  2. Просмотреть вершины в порядке убывания степеней и окрасить первую неокрашенную вершину в цвет № k.

  3. Просмотреть вершины в порядке убывания степеней и окрасить в цвет № k все вершины, которые не смежны вершинам, уже окрашенным в цвет № k .

  4. Если все вершины окрашены, то k — искомое хроматическое число. Иначе k = k + 1, перейти к п. 2.


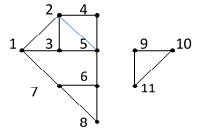
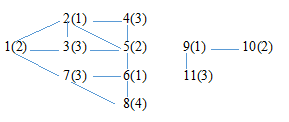
Пусть граф имеет вид:



    1. Рассчитаем степени вершин:

Вершина
1
2
3
4
5
6
7
8
9
10
11

Степень

3
4
3
2
4
3
3
2
2
2
2




    1. Упорядочим вершины по невозрастанию их степеней:


Вершина
2
5
1
3
6
7
4
8
9
10
11

Степень

4
4
3
3
3
3
2
2
2
2
2



    1. k=1


Вершина
2
5
1
3
6
7
4
8
9
10
11

Степень

4
4
3
3
3
3
2
2
2
2
2

Окраска k
1









1









1









    1. k=2


Вершина
2
5
1
3
6
7
4
8
9
10
11

Степень

4
4
3
3
3
3
2
2
2
2
2

Окраска k
1
2
2



1









1
2






    1. k=3


Вершина
2
5
1
3
6
7
4
8
9
10
11

Степень

4
4
3
3
3
3
2
2
2
2
2

Окраска k
1
2
2
3
1
3
3



1
2
3




    1. k=4


Вершина
2
5
1
3
6
7
4
8
9
10
11

Степень

4
4
3
3
3
3
2
2
2
2
2

Окраска k
1
2
2
3
1
3
3
4
1
2
3


Получается, что k=4:



3. Некоторые алгоритмы на графах

3.1. Поиск покрывающего остова (обход вершин графа)


Покрывающий остов (или дерево) – это граф без циклов и петель, покрывающий все вершины исходного графа.

Один из алгоритмов для решения этой задачи - поиск «в глубину» - рассматривался ранее. Теперь рассмотрим алгоритм поиска «в ширину».

Пусть граф G=<X, H> задан списком отображений H={h(xi)}.

Шаг 1: выбрать начальную вершину xi = J, где J – корень дерева (р=1).

Шаг 2: из окружения xi =J выбрать очередную смежную вершину xj(p=p+1) и сформировать фрагмент остова Gi=<Xi, Hi>, использующий подмножество вершин Xi={xi, xj}и прямых ребер T={(xi, xj)}. Повторять шаг 2, пока в списке есть смежные вершины.

Шаг 3: из окрестности вершины xjвыбрать очередную смежную вершину xk∈h(xj) (повторять шаг 3, пока в списке есть смежные вершины):

а) если вершина xkне принадлежит фрагменту остова Gi, то включить ее в множество Xiи сформировать новый фрагмент, использующий подмножество вершин Xi={xi, xj, xk}и прямых ребер T={(xi, xj), (xj, xk)},

b) если вершина xkпринадлежит фрагменту, а ребро (xj, xk) - не принадлежит, то ребро (xj, xk) включить во множество обратных ребер Вi={(xj, xk)}. Эти ребра формируют цикл на графе,

с) если для вершины xjсмежных вершин нет, то вернуться к шагу 3а, выбрав очередную вершину xl, смежную xk,

d) если для вершины xlсмежных вершин нет, то конец алгоритма.
Пример: на рисунке изображен граф, а в таблице – отображение каждой вершины графа.



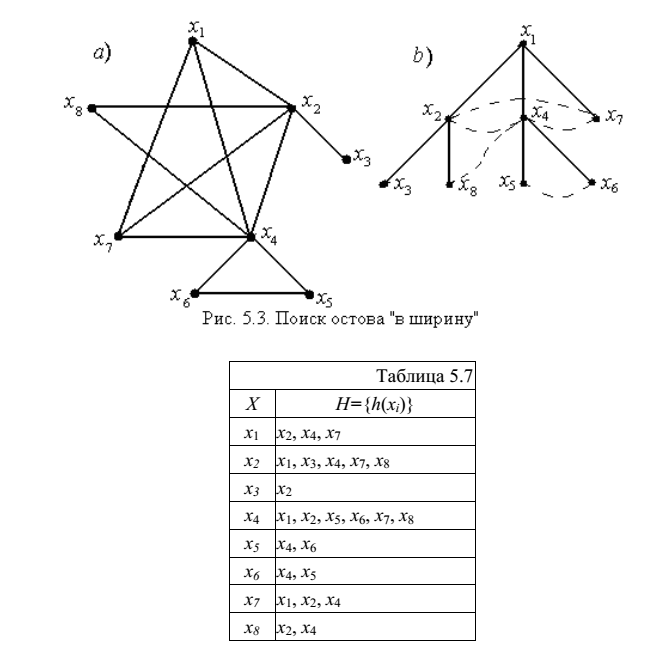
Построить покрывающий остов по алгоритму поиска «в ширину», приняв за начальную вершину – корень дерева – x1
.

Процесс поиска в ширину представлен в таблице:

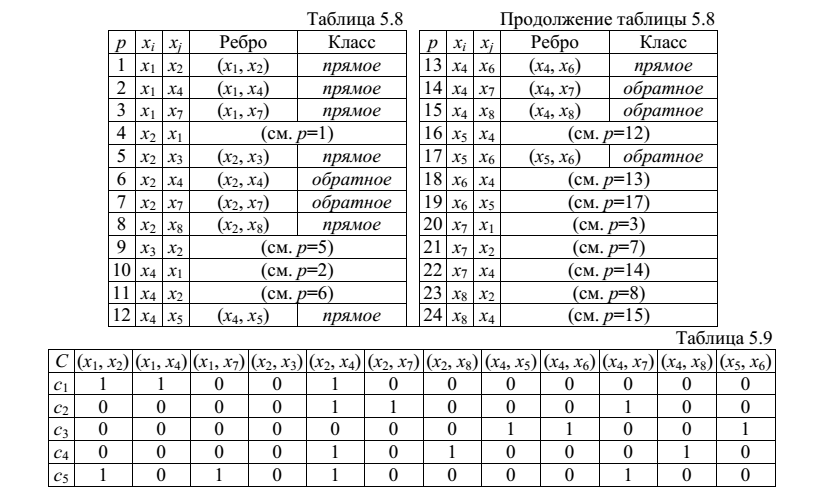
Первые три шага описывают формирование фрагмента остова только из окружения вершины x1. Так как все образы x1 и инцидентные им ребра (x1, x2), (x1, x4), (x1, x7) включены во фрагмент остова, то выбираем из очереди для x1 очередную вершину x2.

Проверим окружение x2: включены ли вершины, смежные x2, во фрагмент остова? Если вершина не включена, то ее и инцидентное ей ребро включить во фрагмент остова. Если вершина включена, то инцидентное ей ребро не включать во фрагмент остова, так как это ребро замыкает цикл на графе. Так обнаружены два прямых ребра (x2, x3), (x2, x8) и два обратных ребра (x2, x4), (x2, x7).

Если все вершины – образы x2 исследованы, то выбираем из очереди вершин, смежных x2, вершину x3. Проверяем окружение x3: включены ли вершины, смежные x3, во фрагмент остова? Для данной вершины нет смежных вершин. Выбираем из очереди вершин, смежных x2, очередную вершину x4. Проверяем окружение x4: включены ли вершины, смежные x4, во фрагмент остова? Да, для вершины x4 есть смежные вершины, включенные во фрагмент остова. Это – вершины x1 и x2. Ребро (x1, x4) – прямое ребро, которое было включено во фрагмент остова при просмотре окружения x1, а ребро (x2, x4) – обратное ребро, которое было обнаружено при просмотре вершины x

Смотрите также файлы