Файл: Точек, являющихся образом множества объектов, и множества линий.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 242
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
)*r(x6,x3)r(x7,x7)*r(x7,x3)=00000=0
R2(х7,х6)=r(x7,x1)*r(x1,x6)r(x7,x2)*r(x2,x6)r(x7,x3)*r(x3,x6)r(x7,x6)*r(x6,x6)r(x7,x7)*r(x7,x6)=01000=1
R2(х7,х7)=r(x7,x1)*r(x1,x7)r(x7,x2)*r(x2,x7)r(x7,x3)*r(x3,x7)r(x7,x6)*r(x6,x7)r(x7,x7)*r(x7,x7)=01110=1
Таким образом, матрица смежности R2 имеет вид:
Матрица достижимости Q2 на этом шаге есть:
Поскольку в матрице достижимости Q2 (р=2) все ячейки заполнены единицами, это означает, что уже на втором шаге стали достижимыми все вершины исходного графа.
Очевидно, для орграфа решение задачи аналогично по матрице смежности.
Функции, заданные на множестве графов {G=} и принимающие значения на множестве целых чисел, называют числовыми характеристиками графа или просто числами графа.
Наиболее очевидными и простыми числами графа являются: число вершин графа (порядок графа) - n, число рёбер или дуг графа (размер графа) - m, степени и полустепени вершин графа - δ (или δ+/δ-).
Все остальные характеристики графа требуют поиска и вычисления их значений.
Если множество вершин графа можно разбить на попарно непересекающиеся непустые подмножества, то существуют связные подграфы1, для которых подмножества ребер инцидентны элементам только одного подмножества вершин. Связные подграфы называют компонентой связности, а их количество – числом компонент связности графа G – k(G).
На рисунке изображен граф G, который содержит 3 не связанных между собой подграфа - G1; G2; G3, т.е. число компонент связности графа G - k(G)=3.
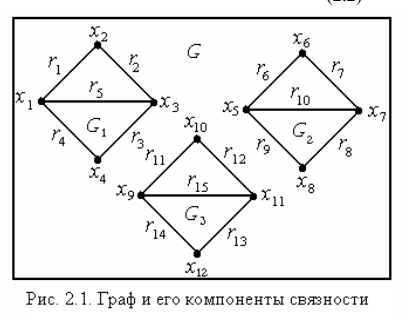
Поиск числа компонент связности графа
Для поиска числа компонент связности k используют матрицы смежности R и матрицы достижимости Qp. Если на некотором шаге матрица достижимости сохраняет свою форму, сформированную на предыдущемшаге, то она считается построенной. Далее, выполняя операцию перестановки строк и столбцов, следует найти на главной диагонали клетки, не содержащие «0».
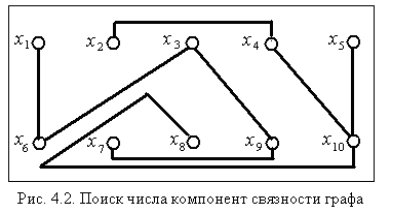
Пример: на рисунке дан граф G=<X, R> , а в таблице -его матрица смежности. Найти число компонент связности k(G):
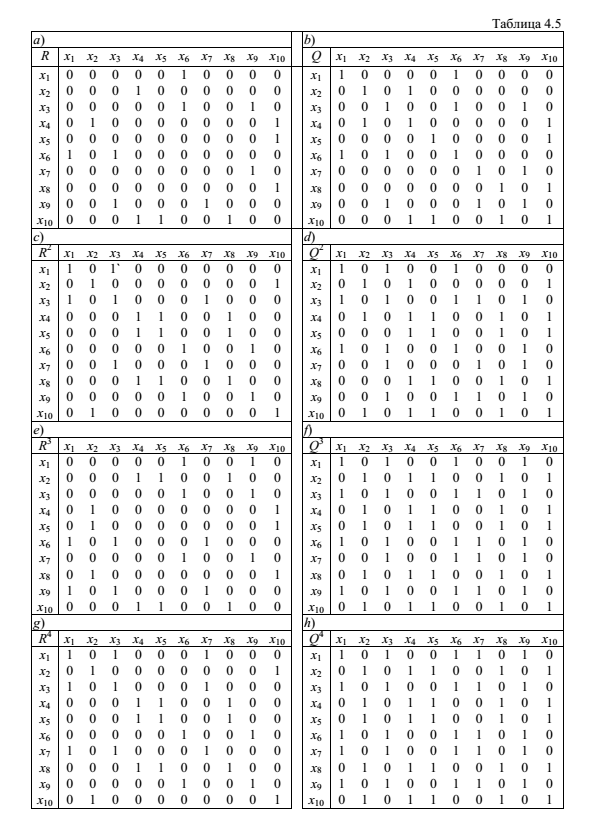
Решение задачи:




Анализ матриц достижимости Q4 и Q5 показывает их полную идентичность. Это означает, что построение матриц достижимости следует закончить;

Видно, что сформированы две клетки, заполненные 1. Это макеты двух подграфов - компонент связности. Значит, k(G) =2.
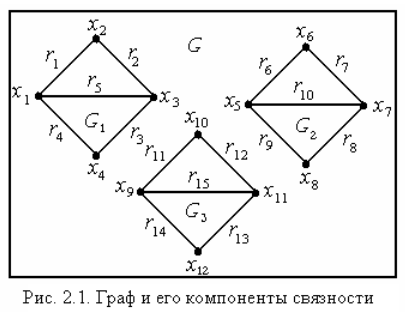
Пример: на рисунке дан граф G=<X, R>. Найти число компонент связности k(G).
Решение задачи:
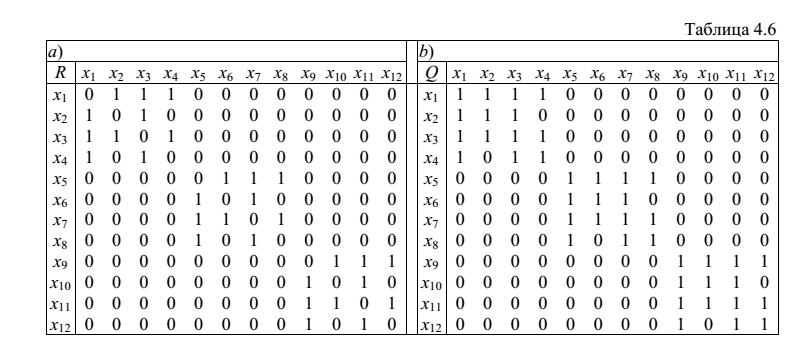

Таблица для Q2 показывает, что любая вершина графа достижима за два шага.
На главной диагонали сформированы 3 клетки, содержащие по четыре вершины графа. Следовательно, k(G)=3.
Наименьшее число рёбер, удаление которых приводит к графу без циклов и петель, называют цикломатическим числом и обозначают (G). Цикломатическое число можно определить по формуле:
(G)=m-n+k(G),
где m - число рёбер, n - число вершин, k(G) - число компонент связности графа.
Для графа G с рисунка n=12, m=15, k(G)=3:

Следовательно, λ(G)=15–12+3=6. Удалив шесть ребер, например, r1, r3, r6, r8, r11, r13, полностью устраняют циклы на графе.
Очевидно, для связного графа цикломатическое число равно λ(G)=m–n+1, т.к. число компонент связности у такого графа – 1.
Поиск удаляемых ребер
Видно, что нахождение цикломатического числа – задача несложная, особенно, если известно число компонент связности графа. Особая проблема – определение удаляемых ребер, чтобы освободить граф от циклов. Для ее решения используется алгоритм поиска «в глубину» остова графа2.
Алгоритм построения дерева произвольного графа включает следующие шаги (граф задан списком отображений h(xi)):
Шаг 1: выбрать начальную вершину xi=J – корень дерева.
Шаг 2:
a) если для вершины xiочередь смежных вершин пуста, то конец алгоритма;
b) иначе из окружения xiвыбрать из очереди смежную вершину xjи сформировать фрагмент остова Gi=<Xi, Hi>, опирающийся на подмножества вершин Xi={xi, xj} и прямых ребер – T={(xi, xj)}, выполнить расчет р=1 (р – шаг итерации алгоритма).
Шаг 3: из окрестности вершины xjвыбрать из очереди смежную вершину xk∈h(xj) (при этом р=p+1):
a) если для вершины xjнет смежных вершин, то отступить на один шаг назад и вернуться к шагу 2, выбрать очередную смежную вершину xl,
b) если вершина xkне принадлежит фрагменту остова Gi, то включить ее в множество
Xi={xi, xj, xk}, а ребро (xj, xk) включить в множество прямых ребер Т={(xi, xj), (xj, xk)}. Принять xj=xk, перейти к шагу 3,
c) если вершина xkпринадлежит фрагменту остова Gi, а ребро не принадлежит, то ребро (xj, xk) включить в множество обратных ребер В={(xj, xk)}; эти ребра формируют циклы на графе. Принять xj=xk, перейти к шагу 3.
Пример: на рисункедан граф, для которого k(G)=1.
Найти цикломатическое число и устранить ребра, создающие циклы.
Решение задачи:
 х1
х1
х2

х1
R2(х7,х6)=r(x7,x1)*r(x1,x6)r(x7,x2)*r(x2,x6)r(x7,x3)*r(x3,x6)r(x7,x6)*r(x6,x6)r(x7,x7)*r(x7,x6)=01000=1
R2(х7,х7)=r(x7,x1)*r(x1,x7)r(x7,x2)*r(x2,x7)r(x7,x3)*r(x3,x7)r(x7,x6)*r(x6,x7)r(x7,x7)*r(x7,x7)=01110=1
Таким образом, матрица смежности R2 имеет вид:
| R2 | х1 | х2 | х3 | х6 | х7 |
| х1 | 1 | 0 | 0 | 1 | 1 |
| х2 | 0 | 1 | 1 | 1 | 1 |
| х3 | 0 | 1 | 1 | 1 | 1 |
| х6 | 1 | 1 | 1 | 1 | 1 |
| х7 | 1 | 1 | 0 | 1 | 1 |
Матрица достижимости Q2 на этом шаге есть:
| Q2 | х1 | х2 | х3 | х6 | х7 |
| х1 | 1 | 1 | 1 | 1 | 1 |
| х2 | 1 | 1 | 1 | 1 | 1 |
| х3 | 1 | 1 | 1 | 1 | 1 |
| х6 | 1 | 1 | 1 | 1 | 1 |
| х7 | 1 | 1 | 1 | 1 | 1 |
Поскольку в матрице достижимости Q2 (р=2) все ячейки заполнены единицами, это означает, что уже на втором шаге стали достижимыми все вершины исходного графа.
Очевидно, для орграфа решение задачи аналогично по матрице смежности.
2. Числа графа и их определение
Функции, заданные на множестве графов {G=
Наиболее очевидными и простыми числами графа являются: число вершин графа (порядок графа) - n, число рёбер или дуг графа (размер графа) - m, степени и полустепени вершин графа - δ (или δ+/δ-).
Все остальные характеристики графа требуют поиска и вычисления их значений.
2.1. Число компонент связности графа
Если множество вершин графа можно разбить на попарно непересекающиеся непустые подмножества, то существуют связные подграфы1, для которых подмножества ребер инцидентны элементам только одного подмножества вершин. Связные подграфы называют компонентой связности, а их количество – числом компонент связности графа G – k(G).
На рисунке изображен граф G, который содержит 3 не связанных между собой подграфа - G1; G2; G3, т.е. число компонент связности графа G - k(G)=3.

Поиск числа компонент связности графа
Для поиска числа компонент связности k используют матрицы смежности R и матрицы достижимости Qp. Если на некотором шаге матрица достижимости сохраняет свою форму, сформированную на предыдущемшаге, то она считается построенной. Далее, выполняя операцию перестановки строк и столбцов, следует найти на главной диагонали клетки, не содержащие «0».
Пример: на рисунке дан граф G=<X, R> , а в таблице -его матрица смежности. Найти число компонент связности k(G):


Решение задачи:
-
найдем матрицу достижимости для исходной матрицы смежности, заменив у нее все элементы на главной диагонали на 1:

-
теперь последовательно, как описано в разделе 1, станем возводить матрицу смежности в степени, начиная со второй, и находить соответствующие матрицы достижимости:



Анализ матриц достижимости Q4 и Q5 показывает их полную идентичность. Это означает, что построение матриц достижимости следует закончить;
-
выполним перестановку строк и одноименных столбцов конечной матрицы достижимости так, чтобы получить клетки, заполненные 1, на главной диагонали. Анализ матрицы Q5 (или Q4) показывает, что такими столбцами и строками могут стать имеющие имена x1,x3,x6,x7,x9 – они содержат 1 в ячейках первой строки. Тогда переставим соответствующие строки и столбцы в первые позиции матрицы, а оставшиеся строки и столбцы оставим после них:

Видно, что сформированы две клетки, заполненные 1. Это макеты двух подграфов - компонент связности. Значит, k(G) =2.
Пример: на рисунке дан граф G=<X, R>. Найти число компонент связности k(G).

Решение задачи:
-
в таблицахприведены матрица смежности R и матрица достижимости Q = I∪R:

-
в таблицах приведены матрица R2, и матрица достижимости Q2 =I∪R∪R2:

Таблица для Q2 показывает, что любая вершина графа достижима за два шага.
На главной диагонали сформированы 3 клетки, содержащие по четыре вершины графа. Следовательно, k(G)=3.
1 2 3 4 5 6 7 8 9 ... 17
2.2. Цикломатическое число графа
Наименьшее число рёбер, удаление которых приводит к графу без циклов и петель, называют цикломатическим числом и обозначают (G). Цикломатическое число можно определить по формуле:
(G)=m-n+k(G),
где m - число рёбер, n - число вершин, k(G) - число компонент связности графа.
Для графа G с рисунка n=12, m=15, k(G)=3:

Следовательно, λ(G)=15–12+3=6. Удалив шесть ребер, например, r1, r3, r6, r8, r11, r13, полностью устраняют циклы на графе.
Очевидно, для связного графа цикломатическое число равно λ(G)=m–n+1, т.к. число компонент связности у такого графа – 1.
Поиск удаляемых ребер
Видно, что нахождение цикломатического числа – задача несложная, особенно, если известно число компонент связности графа. Особая проблема – определение удаляемых ребер, чтобы освободить граф от циклов. Для ее решения используется алгоритм поиска «в глубину» остова графа2.
Алгоритм построения дерева произвольного графа включает следующие шаги (граф задан списком отображений h(xi)):
Шаг 1: выбрать начальную вершину xi=J – корень дерева.
Шаг 2:
a) если для вершины xiочередь смежных вершин пуста, то конец алгоритма;
b) иначе из окружения xiвыбрать из очереди смежную вершину xjи сформировать фрагмент остова Gi=<Xi, Hi>, опирающийся на подмножества вершин Xi={xi, xj} и прямых ребер – T={(xi, xj)}, выполнить расчет р=1 (р – шаг итерации алгоритма).
Шаг 3: из окрестности вершины xjвыбрать из очереди смежную вершину xk∈h(xj) (при этом р=p+1):
a) если для вершины xjнет смежных вершин, то отступить на один шаг назад и вернуться к шагу 2, выбрать очередную смежную вершину xl,
b) если вершина xkне принадлежит фрагменту остова Gi, то включить ее в множество
Xi={xi, xj, xk}, а ребро (xj, xk) включить в множество прямых ребер Т={(xi, xj), (xj, xk)}. Принять xj=xk, перейти к шагу 3,
c) если вершина xkпринадлежит фрагменту остова Gi, а ребро не принадлежит, то ребро (xj, xk) включить в множество обратных ребер В={(xj, xk)}; эти ребра формируют циклы на графе. Принять xj=xk, перейти к шагу 3.
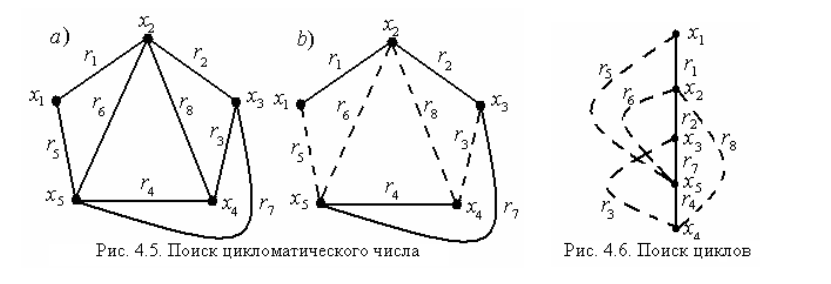
Пример: на рисункедан граф, для которого k(G)=1.

Найти цикломатическое число и устранить ребра, создающие циклы.
Решение задачи:
-
для данного примера m=8, n=5, k(G)=1, следовательно, λ(G)=8–5+1=4, то есть для устранения циклов в графе следует удалить четыре ребра; -
для поиска нужных ребер указанным выше методом опишем граф списком отображений, сведя его в таблицу:
X
H={h(xi)}
x1
x2,x5
x2
x1,x5,x4,x3
x3
x2,x4,x5
x4
x2,x3,x5
x5
x1,x2,x3,x4
-
выберем за корень дерева J (начальную вершину) x1; -
из таблицы отображений для выбранной в п.3 вершины выбираем первую из списка смежных – это вершина х2. Формируем фрагмент остова с прямым ребром:
 х1
х1х2
-
из окрестности вершины х2 выбираем смежную с ней вершину из списка – это вершина х1. Она принадлежит уже построенному остову, также как и ребро (х1,х2). Поэтому выбираем следующую из списка вершину – х5. Достраиваем остов графа:

х1