Файл: Точек, являющихся образом множества объектов, и множества линий.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 239
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ij.
Требования к графу:
Метод СПУ включает, в свою очередь, метод критического пути (МКП), который позволяет найти такую последовательность работ от вершины–истока сети до вершины–стока сети, которая является минимальной среди всех работ, максимальных по продолжительности или по стоимости.
Сеть, представленная на предыдущем рисунке, включает в себя пять вершин–событий и шесть дуг–работ:
Расчет ранних моментов наступления каждого события следует начинать с x0.
При наличии нескольких дуг–работ, исходящих из одной вершины–события, следует определять для каждого события поздний момент его наступления tп(xi) как наименьшее ранее время окончания последующих работ, то есть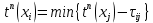 . Расчет поздних моментов наступления каждого события следует начинать с момента окончания всех работ над проектом – xk.Для событий, связанных с ожиданием, ранний и поздний моменты времени вычисляются по формулам:
. Расчет поздних моментов наступления каждого события следует начинать с момента окончания всех работ над проектом – xk.Для событий, связанных с ожиданием, ранний и поздний моменты времени вычисляются по формулам: 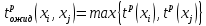 и
и 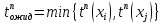 .
.
Последовательность работ от вершины-истока до вершины-стока, которая имеет нулевой резерв времени на каждое событие и работу, т.е.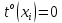 ,
, 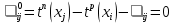 , называется критическим путем сетевой модели.
, называется критическим путем сетевой модели.
Время, на которое можно задержать наступление некоторого события без задержки срока завершения всего проекта, называют резервом времени события, то есть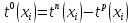 .
.
Время, на которое можно продлить исполнение работы без задержки срока завершения всего проекта, называют резервом времени на работу, то есть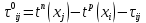 .
.
Алгоритм расчета раннего момента наступления событий:
шаг 1: принять для начальной вершины графа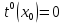 и шаг итерации r = 0,
и шаг итерации r = 0,
шаг 2: определить на шаге итерации rранний момент наступления события xj: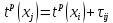 , где
, где 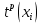 – ранний момент наступления события xi, τij – продолжительность работы от события, имеющего
– ранний момент наступления события xi, τij – продолжительность работы от события, имеющего 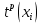 :
:
а) если к вершине xjподходит одна дуга (i, j), то принять ,
,
b) если к вершине xjподходит несколько дуг {(i, j)}, то сравнить их и найти максимальное значение раннего момента наступления события xj: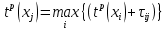 ,
,
шаг 3: если r = (n–1), то конец, иначе принять r= r+1 и перейти к шагу 2.
Алгоритм расчета позднего момента наступления события:
шаг 1: принять для конечной вершины графа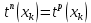 и шаг итерации r= 0,
и шаг итерации r= 0,
шаг 2: определить на шаге итерации rпоздний момент наступления события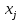 по формуле:
по формуле: 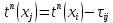 , где
, где 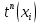 – известный поздний момент наступления события
– известный поздний момент наступления события 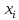 ,
, 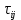 – продолжительность работы (i, j) от события
– продолжительность работы (i, j) от события 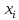 , имеющего
, имеющего 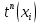 :
:
а) если от вершины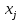 отходит одна дуга (i, j), то принять
отходит одна дуга (i, j), то принять 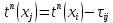 ;
;
b) если от вершины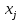 отходит несколько дуг (i, j), то сравнить их и найти минимальное значение позднего момента наступления события
отходит несколько дуг (i, j), то сравнить их и найти минимальное значение позднего момента наступления события 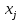 :
: 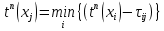 ,
,
шаг 3: если r= (n–1), то конец, иначе принять r= r+1 и перейти к шагу 2.
Алгоритм расчета резерва времени события:
шаг 1: принять r= 0, где r– шаг итерации,
шаг 2: определить на шаге итерации rиндекс события xiи резерв времени на событие: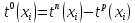 ,
,
шаг 3: если r= (n–1), где n – число вершин, то конец, иначе принять r= r+1 и перейти к шагу 2.
Алгоритм расчета резерва времени на работу:
шаг 1: принять r= 0 и выделить любую дугу (
i, j),
шаг 2: вычислить резерв времени на работу (i, j):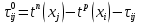 ,
,
шаг 3: если r= m, где m – число дуг, то конец, иначе r= r+1, выделить новую дугу (i,j)и перейти к шагу 2.
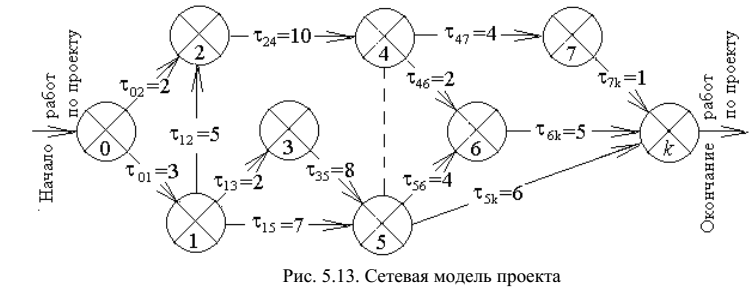
Пример: на рисунке приведена сетевая модель проекта, в которой для компактного изображения параметров каждого события каждая вершина представлена кругом, разделенным на четыре сектора: в одном секторе указан индекс вершины i, в другом – ранний момент события tр(xi), в третьем – поздний момент события tп(xi) и в четвертом – резерв времени на событие t0(xi). Требуется найти критический путь.
Решение задачи разобьем на 4 шага:
Расчет раннего момента наступления каждого события
На решение данной задачи влияет число дуг, входящих в вершину-событие, а также наличие фиктивной работы между вершинами-событиями. В этой связи сгруппируем вершины исходной сети по числу входящих дуг и в соответствии с наличием связи в виде фиктивной работы:
Определим последовательность расчетов в соответствии с исходной сетью и особенностями вершин:
Требования к графу:
-
в графе не должно быть петель и циклов; -
если две или несколько работ должны начинаться одновременно, но привязаны к различным вершинам–истокам, то между этими вершинами должно быть отмечено ожидание (для этого используется пунктирная линия, означающая фиктивную работу.
Метод СПУ включает, в свою очередь, метод критического пути (МКП), который позволяет найти такую последовательность работ от вершины–истока сети до вершины–стока сети, которая является минимальной среди всех работ, максимальных по продолжительности или по стоимости.
Сеть, представленная на предыдущем рисунке, включает в себя пять вершин–событий и шесть дуг–работ:
-
вершина–исток x0 есть начало работ по проекту в момент времени t(x0); -
вершина–сток хkесть окончание всех работ в момент времени t(xk); -
дуги–работы τ01 и τ02 имеют начало в момент времени t(x0); -
вершина–событие х1 есть окончание работы τ01 в момент времени t(x1) = t(x0)+τ01, который определяет возможное начало двух работ τ12 и τ13; -
вершина–событие х2 есть момент окончания двух работ τ02 и τ12. При наличии нескольких дуг–работ, заходящих в одну вершину–событие, следует вычислять для этого события ранний момент его наступления tр(xi) как наиболее позднее окончание всех предшествующих работ, то есть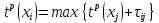 . Поэтому работа τ2kне может начаться раньше
. Поэтому работа τ2kне может начаться раньше 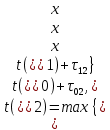 ;
; -
вершина–событие х3 есть окончание работы τ13 в момент времени t(x3) = t(x1)+τ13 и определяет возможность начать работу τ3k. Однако, так как работы τ2k и τ3k должны начаться одновременно, следует найти максимальное время ожидания tожид = max{t(x2), t(x3)} и начать работы одновременно в соответствии с tожид; -
дуги–работы τ2k и τ3k обеспечивают завершение проекта к моменту времени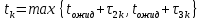 . Следовательно, наибольшая продолжительность работ по проекту есть максимальное значение tk.
. Следовательно, наибольшая продолжительность работ по проекту есть максимальное значение tk.
Расчет ранних моментов наступления каждого события следует начинать с x0.
При наличии нескольких дуг–работ, исходящих из одной вершины–события, следует определять для каждого события поздний момент его наступления tп(xi) как наименьшее ранее время окончания последующих работ, то есть
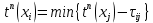 . Расчет поздних моментов наступления каждого события следует начинать с момента окончания всех работ над проектом – xk.Для событий, связанных с ожиданием, ранний и поздний моменты времени вычисляются по формулам:
. Расчет поздних моментов наступления каждого события следует начинать с момента окончания всех работ над проектом – xk.Для событий, связанных с ожиданием, ранний и поздний моменты времени вычисляются по формулам: 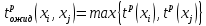 и
и 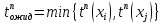 .
.Последовательность работ от вершины-истока до вершины-стока, которая имеет нулевой резерв времени на каждое событие и работу, т.е.
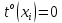 ,
, 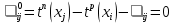 , называется критическим путем сетевой модели.
, называется критическим путем сетевой модели. Время, на которое можно задержать наступление некоторого события без задержки срока завершения всего проекта, называют резервом времени события, то есть
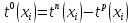 .
.Время, на которое можно продлить исполнение работы без задержки срока завершения всего проекта, называют резервом времени на работу, то есть
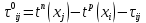 .
.Алгоритм расчета раннего момента наступления событий:
шаг 1: принять для начальной вершины графа
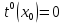 и шаг итерации r = 0,
и шаг итерации r = 0, шаг 2: определить на шаге итерации rранний момент наступления события xj:
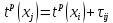 , где
, где 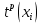 – ранний момент наступления события xi, τij – продолжительность работы от события, имеющего
– ранний момент наступления события xi, τij – продолжительность работы от события, имеющего 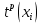 :
:
а) если к вершине xjподходит одна дуга (i, j), то принять
 ,
, b) если к вершине xjподходит несколько дуг {(i, j)}, то сравнить их и найти максимальное значение раннего момента наступления события xj:
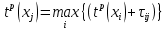 ,
,шаг 3: если r = (n–1), то конец, иначе принять r= r+1 и перейти к шагу 2.
Алгоритм расчета позднего момента наступления события:
шаг 1: принять для конечной вершины графа
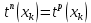 и шаг итерации r= 0,
и шаг итерации r= 0,шаг 2: определить на шаге итерации rпоздний момент наступления события
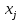 по формуле:
по формуле: 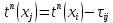 , где
, где 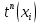 – известный поздний момент наступления события
– известный поздний момент наступления события 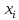 ,
, 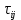 – продолжительность работы (i, j) от события
– продолжительность работы (i, j) от события 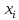 , имеющего
, имеющего 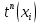 :
:а) если от вершины
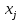 отходит одна дуга (i, j), то принять
отходит одна дуга (i, j), то принять 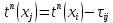 ;
; b) если от вершины
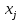 отходит несколько дуг (i, j), то сравнить их и найти минимальное значение позднего момента наступления события
отходит несколько дуг (i, j), то сравнить их и найти минимальное значение позднего момента наступления события 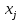 :
: 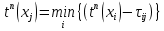 ,
,шаг 3: если r= (n–1), то конец, иначе принять r= r+1 и перейти к шагу 2.
Алгоритм расчета резерва времени события:
шаг 1: принять r= 0, где r– шаг итерации,
шаг 2: определить на шаге итерации rиндекс события xiи резерв времени на событие:
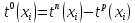 ,
,шаг 3: если r= (n–1), где n – число вершин, то конец, иначе принять r= r+1 и перейти к шагу 2.
Алгоритм расчета резерва времени на работу:
шаг 1: принять r= 0 и выделить любую дугу (
i, j),
шаг 2: вычислить резерв времени на работу (i, j):
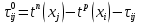 ,
,шаг 3: если r= m, где m – число дуг, то конец, иначе r= r+1, выделить новую дугу (i,j)и перейти к шагу 2.
Пример: на рисунке приведена сетевая модель проекта, в которой для компактного изображения параметров каждого события каждая вершина представлена кругом, разделенным на четыре сектора: в одном секторе указан индекс вершины i, в другом – ранний момент события tр(xi), в третьем – поздний момент события tп(xi) и в четвертом – резерв времени на событие t0(xi). Требуется найти критический путь.

Решение задачи разобьем на 4 шага:
-
расчет раннего момента наступления каждого события; -
расчет позднего времени наступления каждого события; -
расчет резерва времени каждого события; -
расчет резерва времени на исполнение каждой работы и определение критического пути.
Расчет раннего момента наступления каждого события
На решение данной задачи влияет число дуг, входящих в вершину-событие, а также наличие фиктивной работы между вершинами-событиями. В этой связи сгруппируем вершины исходной сети по числу входящих дуг и в соответствии с наличием связи в виде фиктивной работы:
-
вершины с одной входящей дугой – 1, 3, 4, 7: для них ранние моменты наступления событий рассчитываются сразу после определения раннего момента наступления события для вершины-истока; -
вершины с несколькими входящими дугами – 2, 5, 6, k: для них конечный результат рассчитывается только после расчетов ранних моментов наступления событий для всех вершин-истоков и является в некотором смысле «отложенным»; -
вершины, связанные фиктивной работой, – 4 и 5: для них рассчитываются ранние времена наступления событий без учета ожидания и в соответствии с п.1) и 2), а затем полученные значения выравниваются в сторону бόльшего.
Определим последовательность расчетов в соответствии с исходной сетью и особенностями вершин:
-
поскольку вершины 0, 1, 3 формируют переход, можно сначала решить задачу для вершин 1 и 3 (при tp(0)=0):
| r | i | j=h(i) |  |
| 0 | 0 | 1 | 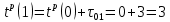 |
| 1 | 1 | 3 | 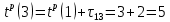 |
-
поскольку определены ранние моменты наступления событий для вершин 1 и 3, можно рассчитать эти характеристики для смежных им вершин 2 и 5 соответственно, которые характеризуются двумя входящими дугами, а вершина 5, кроме того, связана с вершиной 4 фиктивной работой. Это означает, что выполненный на втором этапе расчет для вершины 5 является не окончательным (выделен в таблице желтым цветом) и будет уточнен далее:
| r | i | j=h(i) |  | 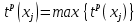 |
| 2 | 0 | 2 | 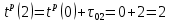 | 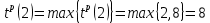 |
| 3 | 1 | 2 | 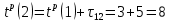 | |
| 4 | 1 | 5 | 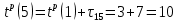 | 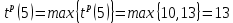 |
| 5 | 3 | 5 | 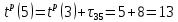 |