Файл: Точек, являющихся образом множества объектов, и множества линий.docx

Пересечение графов

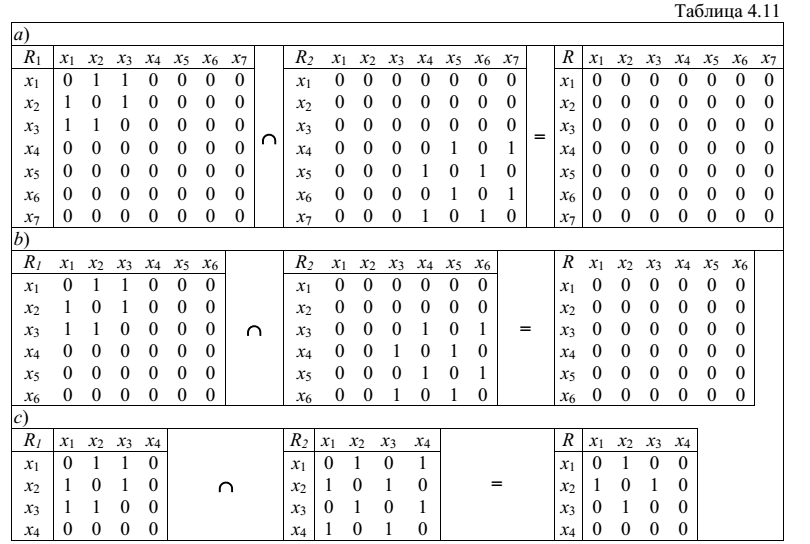
Если есть графы G₁=<X₁, R₁> и G₂=<X₂, R₂>, то их пересечение есть граф G=G₁∩G₂, для которого X=X₁∪X₂ и R=R₁∩R₂:

1. 
   матрицы смежности графов выравнивают по числу строк и столбцов, должны иметь число строк и столбцов, при этом недостающие строки и столбцы заполняют нулями;
   
2. 
   значение элементов матрицы результирующего графа вычисляют по формуле: r(i,j)=r₁(i,j)⋅r₂(i,j).
   

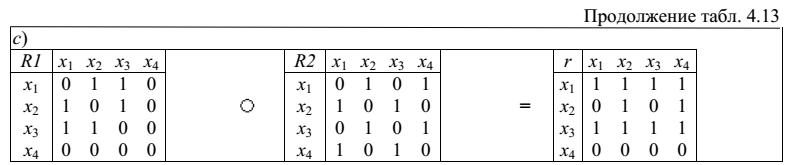
Для приведенных выше примеров вычисления для матриц смежности и графические иллюстрации приведены ниже:

a)





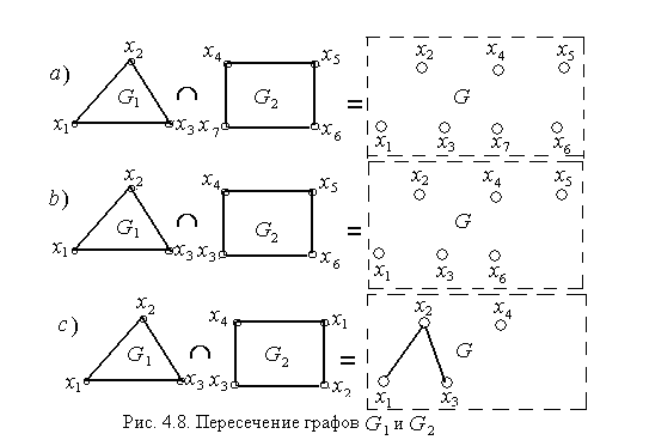
b)





c)





Разность графов

Если есть графы G₁=<X₁, R₁> и G₂=<X₂, R₂ >, то разность графов есть граф G=G₁\G₂, для которого X=X₁∪X₂ и R=R₁\R₂. Разность графов равносильна пересечению графов G₁=<X₁, R₁> и дополнения графа G₂=<X₂, R₂ >.

Тогда для вычисления элементов матрицы смежности графа G следует вычислить матрицу смежности графа ¬G₂ и выполнить операцию пересечения матриц смежности графов G₁ и ¬G₂, то есть r(i,j)=r₁(i,j)⋅

---

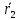(i,j).

Для приведенных выше примеров вычисления для матриц смежности и графические иллюстрации приведены ниже:

a)





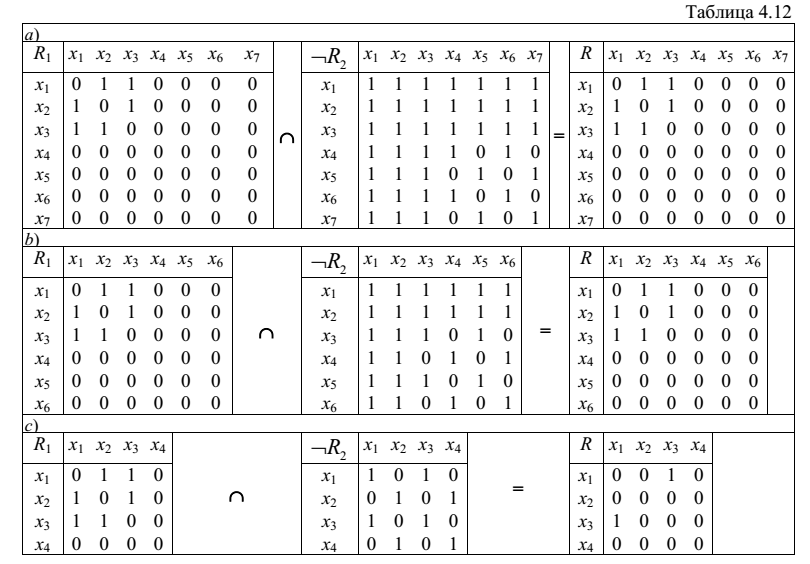
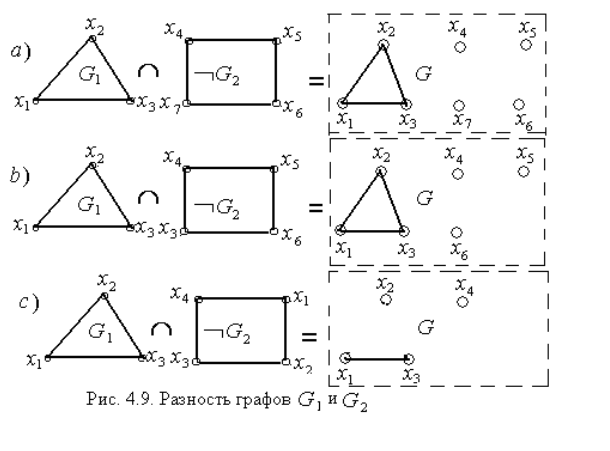
b)





c)





Композиция графов

Если есть графы G₁ и G₂, то композиция этих графов есть граф G= G₁ G₂, для которого Х=Х₁Х₂, а r(i,j)R существует тогда и только тогда, когда графы G₁ и G₂ имеют хотя бы одну вершину x_k, такую, что обеспечивает маршрут с началом в множестве вершин первого графа и концом в множестве вершин второго графа.

Значения элементов матрицы смежности вычисляют по формуле:



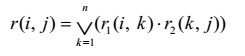
Для примеров вычисления для матриц смежности и графические иллюстрации приведены ниже:

a)




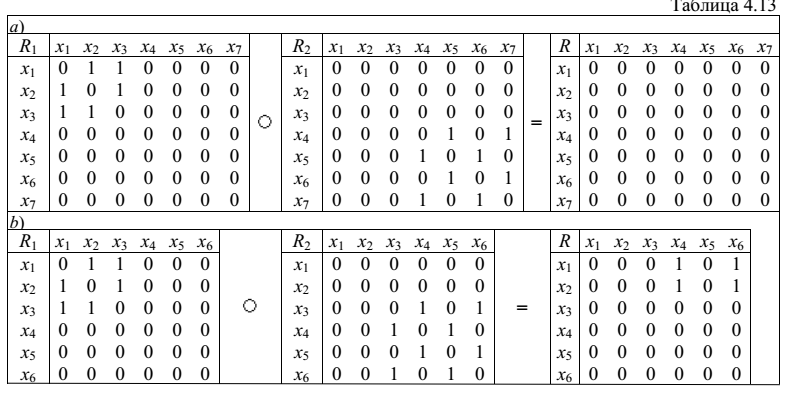
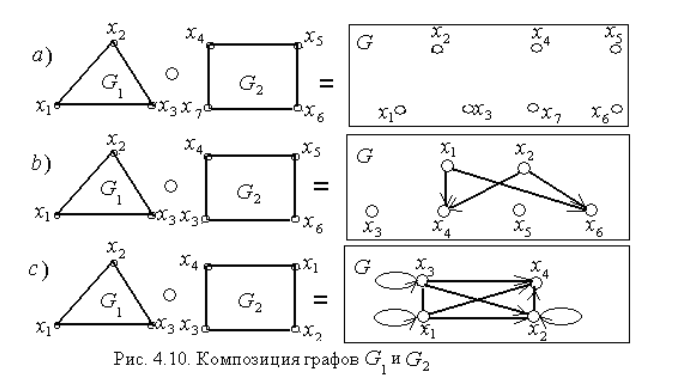
b)




c)

---

Изоморфизм графов

Изоморфизм есть однозначное отображение объектов произвольной природы, выражающее тождество их строения. Для этого необходимо проверить прямое отображение одного объекта на другой и обратное отображение второго объекта на первый.

Пусть даны операторы прямого – h_iи обратного – h_i^-1 отображений вершин и ребер двух графов G₁=<X₁, R₁> и G₂=<X₂, R₂>:

h₁: X₁→X₂, h₂: R₁→R₂,

h₁^-1: X₂→X₁, h₂^-1: R₂ →R₁.

Граф G₁, для которого каждая вершина x_i1∈X₁ и инцидентное ей ребро r₁(i,j)∈R₁ отображаются на графе G₂ вершиной h₁(x_i1)=x_l2∈X₂ и инцидентным ребром h₂(r₁(i,j))=r₂(l,m)∈R₂, называют гомоморфным графу G₂.

Граф G₂, для которого каждая вершина x_i2∈X₂ и инцидентное ей ребро r₂(i,j) ∈R₂ отображаются на графе G₁ вершиной h₁^-1(x_i2)=x_l1∈X₁ и инцидентным ребром h₂^-1(r₂(i, j))=r₁(l,m)∈R₁, называют гомоморфным графу G₁.

Если существует прямой и обратный гомоморфизм для всех вершин графов G₁ и G₂, то они изоморфны.

Пример: на рисунке изображены три графа. Изоморфны ли они?



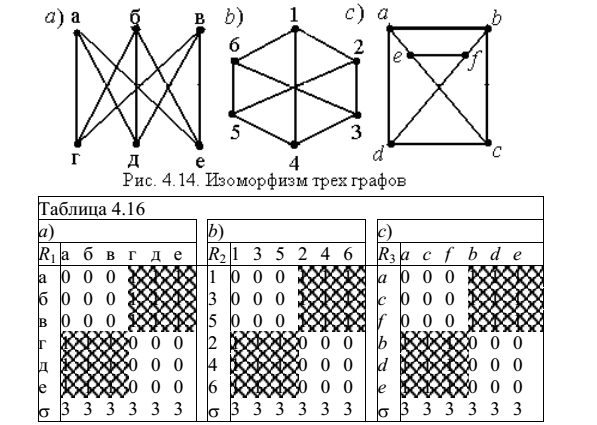
В таблице представлены матрицы смежности этих графов:


Видно, что графы имеют одинаковое число вершин и одинаковые степени вершин, а в результате исполнения операций перестановок строк и столбцов полностью совпадают. Это подтверждает прямой и обратный гомоморфизм каждой пары графов, то есть три графа изоморфны.

Пример: даны два графа:

---

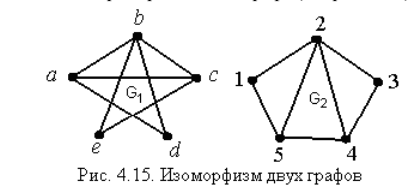
Изоморфны ли они?

В таблице представлены матрицы смежности обоих графов:



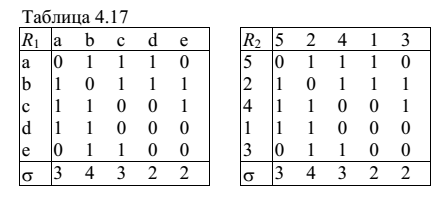
Видно, что матрицы смежности двух графов имеют одинаковое число вершин и одинаковые степени вершин, а в результате исполнения операций перестановки строк и столбцов полностью совпадают. Это подтверждает прямой и обратный гомоморфизм пары графов, то есть они изоморфны.

Это позволяет сделать следующие выводы:

• необходимым условием изоморфизма является равенство числа вершин и ребер, одинаковость числа петель и наборов степеней вершин,

• достаточным условием является одинаковость матриц смежности графов.

---