Файл: Точек, являющихся образом множества объектов, и множества линий.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 237
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Если в качестве базовой использовать последовательно все вершины графа, начиная с х0 до xn, то за p=(n–1) шагов можно найти кратчайшие пути между любой парой вершин.
Алгоритм Флойда включает следующие шаги:
шаг 1: составить матрицу весов и матрицу переходов, принять p=0;
шаг 2: определить вершину p базовой и выделить в матрице весов базовые строку и столбец;
шаг 3: вычеркнуть строки и столбцы матрицы весов, базовые элементы которых имеют значение ∞ (т.к. (lip+∞) и (∞+ lpj) всегда больше конечного значения lij);
шаг 4: сравнить каждый не вычеркнутый небазовый элемент матрицы весов lij с суммой S=lip+lpj: если S< lij, то lij= S, νij= хp,
шаг 5: если p<n, то принять p=p+1 и вернуться к шагу 2, иначе конец.
Пример: найти кратчайшие маршруты между всеми вершинами графа:
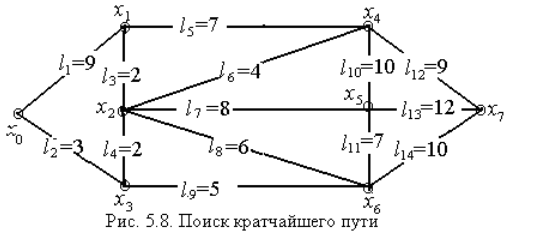
Для начала составим матрицы весов l и переходов :
| l | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 | | | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| x0 | 0 | 9 | | 3 | | | | | | x0 | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| x1 | 9 | 0 | 2 | | 7 | | | | | x1 | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| x2 | | 2 | 0 | 2 | 4 | 8 | 6 | | | x2 | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| x3 | 3 | | 2 | 0 | | | 5 | | | x3 | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| x4 | | 7 | 4 | | 0 | 10 | | 9 | | x4 | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| x5 | | | 8 | | 10 | 0 | 7 | 12 | | x5 | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| x6 | | | 6 | 5 | | 7 | 0 | 10 | | x6 | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| x7 | | | | | 9 | 12 | 10 | 0 | | x7 | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
Примем р = 0 и выделим заливкой в матрице весов базовые столбец и строку:
| L 0 | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| x0 | 0 | 9 | | 3 | | | | |
| x1 | 9 | 0 | 2 | | 7 | | | |
| x2 | | 2 | 0 | 2 | 4 | 8 | 6 | |
| x3 | 3 | | 2 | 0 | | | 5 | |
| x4 | | 7 | 4 | | 0 | 10 | | 9 |
| x5 | | | 8 | | 10 | 0 | 7 | 12 |
| x6 | | | 6 | 5 | | 7 | 0 | 10 |
| x7 | | | | | 9 | 12 | 10 | 0 |
Выделим более плотной заливкой строки и столбцы, для которых базовые элементы которых имеют значение ∞:
| L 0 | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| x0 | 0 | 9 | | 3 | | | | |
| x1 | 9 | 0 | 2 | | 7 | | | |
| x2 | | 2 | 0 | 2 | 4 | 8 | 6 | |
| x3 | 3 | | 2 | 0 | | | 5 | |
| x4 | | 7 | 4 | | 0 | 10 | | 9 |
| x5 | | | 8 | | 10 | 0 | 7 | 12 |
| x6 | | | 6 | 5 | | 7 | 0 | 10 |
| x7 | | | | | 9 | 12 | 10 | 0 |
Остались не вычеркнутыми элементы l13= и l31=. Поскольку матрица симметрична относительно главной диагонали, можно работать только с одним из элементов, например, с l13: l10+l03=9+3=12. Так как 12<, согласно алгоритму выполняем действия: l13=12 и ν13 = х0 (измененные элементы выделены красным):
| L 1 | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 | | 1 | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| x0 | 0 | 9 | | 3 | | | | | | x0 | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| x1 | 9 | 0 | 2 | 12 | 7 | | | | | x1 | x0 | x1 | x2 | x0 | x4 | x5 | x6 | x7 |
| x2 | | 2 | 0 | 2 | 4 | 8 | 6 | | | x2 | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| x3 | 3 | 12 | 2 | 0 | | | 5 | | | x3 | x0 | x0 | x2 | x3 | x4 | x5 | x6 | x7 |
| x4 | | 7 | 4 | | 0 | 10 | | 9 | | x4 | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| x5 | | | 8 | | 10 | 0 | 7 | 12 | | x5 | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| x6 | | | 6 | 5 | | 7 | 0 | 10 | | x6 | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| x7 | | | | | 9 | 12 | 10 | 0 | | x7 | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
1 ... 6 7 8 9 10 11 12 13 ... 17
При р=1 меняем базовый элемент и выполняем аналогичные исследования:
| L 1 | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| x0 | 0 | 9 | | 3 | | | | |
| x1 | 9 | 0 | 2 | 12 | 7 | | | |
| x2 | | 2 | 0 | 2 | 4 | 8 | 6 | |
| x3 | 3 | 12 | 2 | 0 | | | 5 | |
| x4 | | 7 | 4 | | 0 | 10 | | 9 |
| x5 | | | 8 | | 10 | 0 | 7 | 12 |
| x6 | | | 6 | 5 | | 7 | 0 | 10 |
| x7 | | | | | 9 | 12 | 10 | 0 |