Файл: Точек, являющихся образом множества объектов, и множества линий.docx

Матрица смежности

Это квадратная матрица, число строк и столбцов которой равно |X|=n. Элементы матрицы смежности определяют по формуле:



В таблице описана матрица смежности неографа:

	v1	v2	v3	v4
v1	0	0	1	0
v2	0	0	1	1
v3	1	1	0	0
v4	0	1	0	1

В таблице дана матрица смежности орграфа:

	х1	х2	х3	х4	х5	σ+
х1	0	1	0	0	0	1
х2	0	0	1	0	0	1
х3	0	0	0	1	1	2
х4	1	1	0	0	0	2
х5	0	1	0	0	0	1
σ-	1	3	1	1	1

---

Строками в этой таблице заданы вершины-истоки, а столбцами – вершины-стоки. Поэтому столбец σ+ показывает полустепени вершин-истоков, а строка σ^- – полустепени вершин-стоков.

По матрицам смежности ориентированного и неориентированного графов можно сделать следующие выводы:

• матрица смежности неориентированного графа симметрична относительно главной диагонали, а ориентированного графа - несимметрична,

• столбец ориентированного графа, все элементы которого имеют значение «0», определяет общую вершину-исток связного графа,

• строка ориентированного графа, все элементы которой имеют значение «0», определяет общую вершину-сток связного графа,

• каждый ненулевой элемент главной диагонали соответствует петле на графе.

Матрица достижимости

В отличие от других способов описания графа она содержит производные данные, которые формируются на основе матрицы смежности, - информацию о путях между вершинами графа:

1. 
   отображение h(x_i)={x_j} - есть множество вершин окрестности вершины x_i, достижимых из x_iза «один шаг», представляется матрицей смежности;
   
2. 
   отображение h(h(x_i))=h²(x_i) есть множество вершин, достижимых из x_iза «два шага» через промежуточные вершины «первого шага»;
   
3. 
   отображение h(h(h(x_i)))=h³(x_i) формирует множество вершин, достижимых из вершины x_iза «три шага» через промежуточные вершины «второго» шага и т.д.;
   
4. 
   любая вершина связного графа достижима за p≤n шагов.
   

Матрица достижимости Q^p вычисляется по формуле:

Q^p = I ∪ R∪ R²∪ R³∪..∪ R^p,

где R^p– матрица смежности в степени р,

R – исходная матрица смежности,

I – единичная матрица, в которой элементы главной диагонали равны «1», а вне ее – «0».

Единичное значение элементов матрицы смежности в степени p свидетельствуют о достижимости из вершины x_iвершины x_jна p–м шаге.

При возведении в степень матрицы смежности используют правило умножения булевых матриц:

---

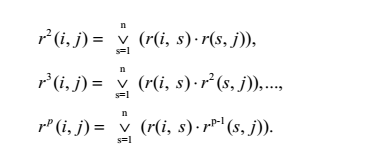
Элементы матрицы достижимости вычисляются по правилам булевой алгебры:

• 
  для исходной матрицы смежности R: q(i,j)=1 при i=j и q(i,j)=r(i,j) при ij;
  
• 
  для матриц смежности в степени р: q(i,j)^p=q(i,j)^(p-1)r(i,j)^p.
  

Единичные значения элементов матрицы достижимости в степени p, то есть q(i,j)^p=1, свидетельствуют о достижимости из вершины i вершины j на любом шаге до p–го включительно.
Пример: в таблице дана матрица смежности R некоторого неориентированного графа (предлагается построить его самостоятельно).

Определить достижимость каждой вершины графа.

R	х1	х2	х3	х6	х7
х1	0	1	1	0	0
х2	1	0	0	1	1
х3	1	0	0	0	1
х6	0	1	0	0	1
х7	0	1	1	1	0

Матрица достижимости для нее имеет вид (она отличается от исходной матрицы смежности только наличием 1 на главной диагонали):

Q	х1	х2	х3	х6	х7
х1	1	1	1	0	0
х2	1	1	0	1	1
х3	1	0	1	0	1
х6	0	1	0	1	1
х7	0	1	1	1	1

---

Рассчитаем последующие степени матрицы смежности по приведенным правилам булевой алгебры:

R²(х₁,х₁)=r(x₁,x₁)*r(x₁,x₁)r(x₁,x₂)*r(x₂,x₁)r(x₁,x₃)*r(x₃,x₁)r(x₁,x₆)*r(x₆,x₁)r(x₁,x₇)*r(x₇,x₁)=01100=1

R²(х₁,х₂)=r(x₁,x₁)*r(x₁,x₂)r(x₁,x₂)*r(x₂,x₂)r(x₁,x₃)*r(x₃,x₂)r(x₁,x₆)*r(x₆,x₂)r(x₁,x₇)*r(x₇,x₂)=00000=0

R²(х₁,х₃)=r(x₁,x₁)*r(x₁,x₃)r(x₁,x₂)*r(x₂,x₃)r(x₁,x₃)*r(x₃,x₃)r(x₁,x₆)*r(x₆,x₃)r(x₁,x₇)*r(x₇,x₃)=00000=0

R²(х₁,х₆)=r(x₁,x₁)*r(x₁,x₆)r(x₁,x₂)*r(x₂,x₆)r(x₁,x₃)*r(x₃,x₆)r(x₁,x₆)*r(x₆,x₆)r(x₁,x₇)*r(x₇,x₆)=01000=1

R²(х₁,х₇)=r(x₁,x₁)*r(x₁,x₇)r(x₁,x₂)*r(x₂,x₇)r(x₁,x₃)*r(x₃,x₇)r(x₁,x₆)*r(x₆,x₇)r(x₁,x₇)*r(x₇,x₇)=01100=1

R²(х₂,х₁)=r(x₂,x₁)*r(x₁,x₁)r(x₂,x₂)*r(x₂,x₁)r(x₂,x₃)*r(x₃,x₁)r(x2,x6)*r(x₆,x₁)r(x₂,x₇)*r(x₇,x₁)=00000=0

R²(х₂,х₂)=r(x₂,x₁)*r(x₁,x₂)r(x₂,x₂)*r(x₂,x₂)r(x₂,x₃)*r(x₃,x₂)r(x₂,x₆)*r(x₆,x₂)r(x₂,x₇)*r(x₇,x₂)=10011=1

R²(х₂,х₃)=r(x₂,x₁)*r(x₁,x₃)r(x₂,x₂)*r(x₂,x₃)r(x₂,x₃)*r(x₃,x₃)r(x₂,x₆)*r(x₆,x₃)r(x₂,x₇)*r(x₇,x₃)=10001=1

R²(х₂,х₆)=r(x₂,x₁)*r(x₁,x₆)r(x₂,x₂)*r(x₂,x₆)r(x₂,x₃)*r(x₃,x₆)r(x₂,x₆)*r(x₆,x₆)r(x₂,x₇)*r(x₇,x₆)=00001=1

R²(х₂,х₇)=r(x₂,x₁)*r(x₁,x₇)r(x₂,x₂)*r(x₂,x₇)r(x₂,x₃)*r(x₃,x₇)r(x₂,x₆)*r(x₆,x₇)r(x₂,x₇)*r(x₇,x₇)=00011=1

R²(х₃,х₁)=r(x₃,x₁)*r(x₁,x₁)r(x₃,x₂)*r(x₂,x₁)r(x₃,x₃)*r(x₃,x₁)r(x₃,x₆)*r(x₆,x₁)r(x₃,x₇)*r(x₇,x₁)=00000=0

R²(х₃,х₂)=r(x

---

₃,x₁)*r(x₁,x₂)r(x₃,x₂)*r(x₂,x₂)r(x₃,x₃)*r(x₃,x₂)r(x₃,x₆)*r(x₆,x₂)r(x₃,x₇)*r(x₇,x₂)=10001=1

R²(х₃,х₃)=r(x₃,x₁)*r(x₁,x₃)r(x₃,x₂)*r(x₂,x₃)r(x₃,x₃)*r(x₃,x₃)r(x₃,x₆)*r(x₆,x₃)r(x₃,x₇)*r(x₇,x₃)=10001=1

R²(х₃,х₆)=r(x₃,x₁)*r(x₁,x₆)r(x₃,x₂)*r(x₂,x₆)r(x₃,x₃)*r(x₃,x₆)r(x₃,x₆)*r(x₆,x₆)r(x₃,x₇)*r(x₇,x₆)=00001=1

R²(х₃,х₇)=r(x₃,x₁)*r(x₁,x₇)r(x₃,x₂)*r(x₂,x₇)r(x₃,x₃)*r(x₃,x₇)r(x₃,x₆)*r(x₆,x₇)r(x₃,x₇)*r(x₇,x₇)=00001=1

R²(х₆,х₁)=r(x₆,x₁)*r(x₁,x₁)r(x₆,x₂)*r(x₂,x₁)r(x₆,x₃)*r(x₃,x₁)r(x₆,x₆)*r(x₆,x₁)r(x₆,x₇)*r(x₇,x₁)=01000=1

R²(х₆,х₂)=r(x₆,x₁)*r(x₁,x₂)r(x₆,x₂)*r(x₂,x₂)r(x₆,x₃)*r(x₃,x₂)r(x₆,x₆)*r(x₆,x₂)r(x₆,x₇)*r(x₇,x₂)=00001=1

R²(х₆,х₃)=r(x₆,x₁)*r(x₁,x₃)r(x₆,x₂)*r(x₂,x₃)r(x₆,x₃)*r(x₃,x₃)r(x₆,x₆)*r(x₆,x₃)r(x₆,x₇)*r(x₇,x₃)=00001=1

R²(х₆,х₆)=r(x₆,x₁)*r(x₁,x₆)r(x₆,x₂)*r(x₂,x₆)r(x₆,x₃)*r(x₃,x₆)r(x₆,x₆)*r(x₆,x₆)r(x₆,x₇)*r(x₇,x₆)=01001=1

R²(х₆,х₇)=r(x₆,x₁)*r(x₁,x₇)r(x₆,x₂)*r(x₂,x₇)r(x₆,x₃)*r(x₃,x₇)r(x₆,x₆)*r(x₆,x₇)r(x₆,x₇)*r(x₇,x₇)=01000=1

R²(х₇,х₁)=r(x₇,x₁)*r(x₁,x₁)r(x₇,x₂)*r(x₂,x₁)r(x₇,x₃)*r(x₃,x₁)r(x₇,x₆)*r(x₆,x₁)r(x₇,x₇)*r(x₇,x₁)=01100=1

R²(х₇,х₂)=r(x₇,x₁)*r(x₁,x₂)r(x₇,x₂)*r(x₂,x₂)r(x₇,x₃)*r(x₃,x₂)r(x₇,x₆)*r(x₆,x₂)r(x₇,x₇)*r(x₇,x₂)=00010=1

R²(х₇,х₃)=r(x₇,x₁)*r(x₁,x₃)r(x₇,x₂)*r(x₂,x₃)r(x₇,x₃)*r(x₃,x₃)r(x₇,x₆

---