Файл: Точек, являющихся образом множества объектов, и множества линий.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 244
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Калининградский государственный технический университет»
О.М. ТОПОРКОВА
ОСНОВЫ ТЕОРИИ ГРАФОВ
Калининград
Издательство ФГБОУ ВО «КГТУ»
2020
Оглавление
1. Граф и его характеристики 3
1.1.Основные понятия 3
1.2. Описание графа 4
2. Числа графа и их определение 12
2.1. Число компонент связности графа 12
2.2. Цикломатическое число графа 16
2.3. Плотность графа 19
2.4 Хроматическое число графа 23
3. Некоторые алгоритмы на графах 27
3.1. Поиск покрывающего остова (обход вершин графа) 27
3.2. Поиск остова минимального веса 30
3.3. Поиск кратчайших путей в графе 34
3.4. Поиск критического пути в графе 47
4. Операции на графах 57
1. Граф и его характеристики
-
Основные понятия
Совокупность объектов произвольной природы и отношений между ними может быть изображена на плоскости в виде множества точек, являющихся образом множества объектов, и множества линий, соединяющих пары точек, что является образом множества отношений. Такое представление принято называть графом G.
Используются разные способы обозначения графа, например:
-
G=,
где Х={xi} - множество точек, элементы которого называют вершинами графа (носитель графа),
R= {rj=(xi,xk)|xi,xkX} – множество линий, соединяющих точки (сигнатура графа): линии представляют неупорядоченную или упорядоченную пару элементов множества Х: в первом случае линия называется ребром графа, во втором - дугой;
-
G=,
где Х={xi} – вершины графа,
H={h(xi)={xj}|xi,xjX} – множество образов (окружение) вершины xi.
Некоторые понятия графа:
-
порядок графа n - число вершин; -
размер графа m- число линий. Если различные линии соответствуют одним и тем же парам вершин графа, они называются кратными; -
петля - линия, соединяющая вершину саму с собой; -
концевые точки (концы) линии – вершины, между которыми проходит линия; в этом случае линия инцидентнасвоим концевымвершинам, которые, в свою очередь, инцидентнылинии; -
степень (валентность) вершины δ - число линий, инцидентных вершине; -
если линия является дугой rj=(xi,xk), то:
-
xi - начальная вершина, или исток, дуги (дуга выходит из вершины xi), в этом случае говорят о положительной инцидентности вершины, а число дуг, исходящих из нее, называют полустепенью вершины δ+; -
xk конечная вершина, или сток, дуги (дуга входит в вершину xk), в этом случае говорят об отрицательной инцидентности вершины, а число дуг, заходящих в нее, также называют полустепенью вершины и обозначают δ-;
-
смежные вершины - концевые точки одной линии; -
смежные линии - линии, имеющие общую вершину; -
маршрут (xi, xj) - последовательность смежных линий, соединяющих вершины xi и xj , количество линий - длина маршрута l. Длину минимального маршрута называют расстоянием. Маршрут может быть:
-
простым, если при его обходе каждая промежуточная вершина встречается не более 1 раза; -
цепью, если при его обходе каждая линия встречается не более одного раза; -
открытым, если его концевые вершины различны; -
замкнутым, если его концевые вершины совпадают; -
циклом – когда он является замкнутой цепью;
-
переход ν(xi, xj) - последовательность смежных вершин цепи, соединяющей несмежные вершины графа xiи xj,.
Виды графов:
-
смешанный - среди линий есть и дуги, и ребра; -
простой (обыкновенный) - не имеет ни петель, ни кратных линий; -
псевдограф - имеет кратные линии и петли; -
ориентированный граф (орграф) – его линии являются либо дугами, либо петлями; -
неориентированный граф (неограф) – его линии являются только ребрами либо петлями; -
связный - любые две вершины можно соединить маршрутом, т.е. каждая вершина графа достижима; -
эйлеров- все вершины его достижимы и степень каждой вершины есть четное число; -
полный – все вершины смежны между собой; -
пустой - любые две его вершины несмежные (это граф без линий); -
подграф - порождён из некоторого графа подмножеством его вершин вместе с инцидентными им линиями; -
частичный граф - порождён из некоторого графа подмножеством его линий вместе с инцидентными им вершинами; -
суграф – порожден из некоторого графа подмножеством его линий, но использует все его вершины; -
остов, или дерево, - суграф без циклов, петель и кратных ребер; -
взвешенный граф - его линии или вершины имеют дополнительные (весовые) характеристики
1.2. Описание графа
Граф может быть задан списками отображений или отношений, матрицей инцидентности, матрицей смежности.
Списки
Пусть есть неограф на рисунке:
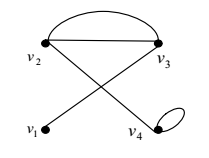
Список отображений для него:
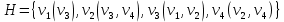 .
.Список отношений: R={r1(v1,v3), r2(v2,v3), r3(v2,v3), r4(v2,v4), r5(v4,v4)}.
Пусть есть орграф:
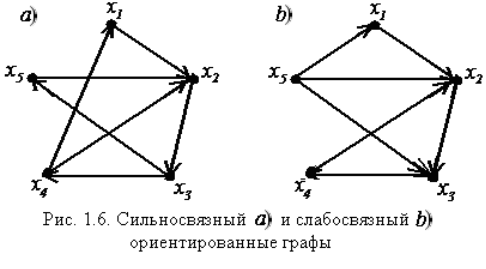
Список отображений для него:
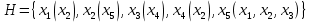 ,
,Список отношений: R={r1(x1,x2), r2(x2,x3), r3(x3,x4), r4(x4,x2), r5(x5,x1), r6(x5,x2), r7(x5,x3)}.
Матрица инцидентности
Матрица инцидентности описывает связь линий графа (строки матрицы) и его вершин (столбцы матрицы).
Для неографа отношение принадлежности вершины графа его ребру определяют по формуле:
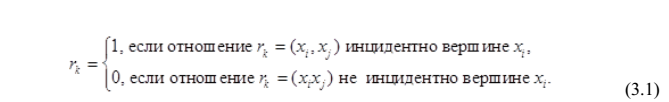
В каждой строке матрицы количество единиц равно двум, так как это есть концевые вершины ребра, а в каждом столбце - степени вершины - δ. Если граф содержит петлю относительно вершины xi, то в строке соответствующего отношения будет «1» только для вершины xi.
В таблице приведена матрица инцидентности для графа предыдущего примера:
| | v1 | v2 | v3 | v4 |
| r1 | 1 | 0 | 1 | 0 |
| r2 | 0 | 1 | 1 | 0 |
| r3 | 0 | 1 | 1 | 0 |
| r4 | 0 | 1 | 0 | 1 |
| r5 | 0 | 0 | 0 | 1 |
Для орграфа отношение инцидентности определяют по формуле:
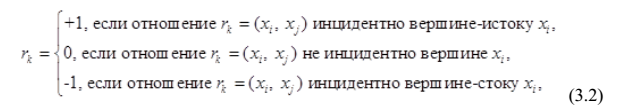
В каждой строке должны быть один символ «+1» и один «–1», а в каждом столбце сумма «+1» равна полустепени исхода вершины xi, а сумма «–1» – полустепени захода вершины xi.
Таблица описывает матрицу инцидентности орграфа:

| | x1 | x2 | x3 | x4 | x5 |
| r1 | +1 | -1 | 0 | 0 | 0 |
| r2 | 0 | +1 | -1 | 0 | 0 |
| r3 | 0 | -1 | 0 | 0 | +1 |
| r4 | 0 | 0 | +1 | 0 | -1 |
| r5 | 0 | 0 | +1 | -1 | 0 |
| r6 | 0 | -1 | 0 | +1 | 0 |
| r7 | -1 | 0 | 0 | +1 | 0 |