ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.04.2021
Просмотров: 2198
Скачиваний: 4
80
очередь, естественного отбора) в формировании динамики генетической структуры
и численности популяций, живущих в условии ограниченности жизненных ресурсов.
Развитие этих идей получило продолжение во многих работах, и было сформули-
ровано в виде концепции K-r-отбора (напр., в [4-6]). Во-вторых, это необходимость
анализа последствий промысла, поскольку эксплуатируе-мые популяции находятся
в других экологических условиях относительно неэксплуатируемых; в результате
чего условия естественного отбора и приспособленности генотипических групп мо-
гут измениться из-за промысловых воздействий [7]. Вместе с тем, многие свойства
популяции определяются особенностями ее возрастной структуры. Глубокое пони-
мание результатов действия внутрипопуляционных механизмов самоорганизации в
структурированной популяции необходимо для дальнейшего исследования того, что
происходит с биологической популяцией при изменении факторов внешней среды
(например, промысле); тем более, что многие ценные промысловые виды имеют
сложную возрастную структуру. Для моделирования динамики таких популяций
разработаны и активно используются матричные модели [8-15 и др.], которые поз-
воляют детально описать возрас-тную структуру популяции и определить ее роль и
значение в поддержа-нии и эволюции популяционных циклов [16-19]. Исследование
изменений в генетической структуре и поведении численности структурированной
популяции, связанных с действием эволюционных факторов (в первую очередь, есте-
ственным отбором), на данный момент остается слабо проработанным. В ходе пред-
ставленной работы продолжается исследование эволюции структурированной попу-
ляции. Рассматривается достаточно простая модельная ситуация, когда популяцию
составляют две возрастные группы и один из ее экологических параметров опреде-
ляется генетически с учетом Менделевских законов наследования. Такой более де-
тальный модельный подход позволяет заглянуть внутрь эволюционных процессов
и выявить ряд неочевидных внутренних свойств, присущих эволюции структури-
рованной популяции, которые остаются неосвещенными в рамках экологического
моделирования.
1.
Модель эволюции двухвозрастной
популяции
Рассмотрим двухвозрастную популяцию [20], в которой выживаемость особей
репродуктивной группы, определяется генетически. Предположим, что адаптивный
параметр
c
кодируется одним диаллельным локусом с аллеломорфами
A
и
a
; в попу-
ляции наблюдается панмиксия гамет (с равной гаметопродукцией для всех геноти-
пов). Естественный отбор действует на половозрелых особей, а именно дифференци-
рует выживаемость особей репродуктивного возраста при переходе к следующему
сезону размножения. Поставим в соответствие каждому генотипу (
AA
,
Aa
и
aa
) по
коэффициенту
c
AA
,
c
Aa
и
c
aa
, характеризующему выживаемость половозрелых осо-
бей соответствующего генотипа при переходе к следующему сезону размножения, и
будем называть эти коэффициенты приспособленностью соответствующего геноти-
па (или выживаемостью этого генотипа репродуктивной группы). Этих предполо-
жений достаточно, чтобы получить следующую систему уравнений, связывающих
численности возрастных классов и генетический состав популяции в последователь-
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
81
ных поколениях:
x
n
+1
=
wy
n
y
n
+1
=
x
n
(1
−
x
n
) + ¯
c
n
y
n
q
n
+1
=
p
AA,n
+
1
2
p
Aa,n
p
AA,n
+1
=
x
n
(1
−
x
n
)
q
2
n
+
y
n
c
AA
p
AA,n
x
n
(1
−
x
n
) + ¯
c
n
y
n
p
Aa,n
+1
=
2
x
n
(1
−
x
n
)
q
n
(1
−
q
n
) +
y
n
c
Aa
p
Aa,n
x
n
(1
−
x
n
) + ¯
c
n
y
n
(1)
где
x
и
y
- это численность неполовозрелой и репродуктивной возрастной группы,
соответственно;
w
- репродуктивный потенциал популяции;
q
– частота аллеля
A
в
младшей возрастной группе,
p
AA
и
p
Aa
- частоты генотипов
AA
и
Aa
в репродуктив-
ной части популяции,
¯
c
- средняя выживаемость репродуктивной группы при пере-
ходе к следующим сезонам размножения:
¯
c
n
= (
c
AA
−
c
aa
)
p
AA,n
+(
c
Aa
−
c
aa
)
p
Aa,n
+
c
aa
.
Заметим, что введение естественного отбора на более поздней стадии жизненного
цикла приводит к усложнению модели, т.е. к добавлению еще одного уравнения (от-
носительно модели двухвозрастной популяции с отбором по приспособленностям за-
родышей). Поскольку естественный отбор нарушает равновесие Харди-Вайнберга в
репродуктивной части популяции, полное описание эволюции генетической структу-
ры популяции в одних только частотах аллелей становится невозможным и возника-
ет необходимость вводить уравнения, описывающие динамику уже генотипических
частот в старшей возрастной группе.
2.
Результаты исследования
Проведенное исследование устойчивости стационарных точек модели (1) позво-
лило заключить, что генетический состав популяции определяется взаимным распо-
ложением выживаемостей половозрелых особей
c
ij
, а динамический режим величи-
ной репродуктивного потенциала
w
вместе с коэффициентом
¯
c
. Генетический состав
популяции, а именно, будет ли она полиморфной или мономорфной, в большей сте-
пени зависит от соотношения выживаемостей гетерозиготы (
c
Aa
) и гомозигот (
c
AA
,
c
aa
). Также выживаемости генотипов, присутствующих в популяции, определяют
среднюю выживаемость репродуктивной группы
¯
c
, и уже эта величина вместе с ре-
продуктивным потенциалом (
w
) определяет тип режима динамики численности по-
пуляции. Можно ожидать, что как и в предыдущем случае (модель двухвозрастной
популяции с отбором по приспособленностям зародышей), при достаточной вели-
чине репродуктивного потенциала (
w
) рост средней выживаемости репродуктивной
группы (
¯
c
) приведет к возникновению колебаний численности и (если популяция по-
лиморфна) генетического состава популяции. Вопрос о том, как именно происходит
увеличение
¯
c
, не является тривиальным. Рассматриваемая модель демонстрирует
как минимум два различных эволюционных сценария изменения динамики популя-
ции, обусловленных ростом выживаемости генотипов. Так рост средней выживаемо-
сти репродуктивной группы
¯
c
способен дестабилизировать динамику численности
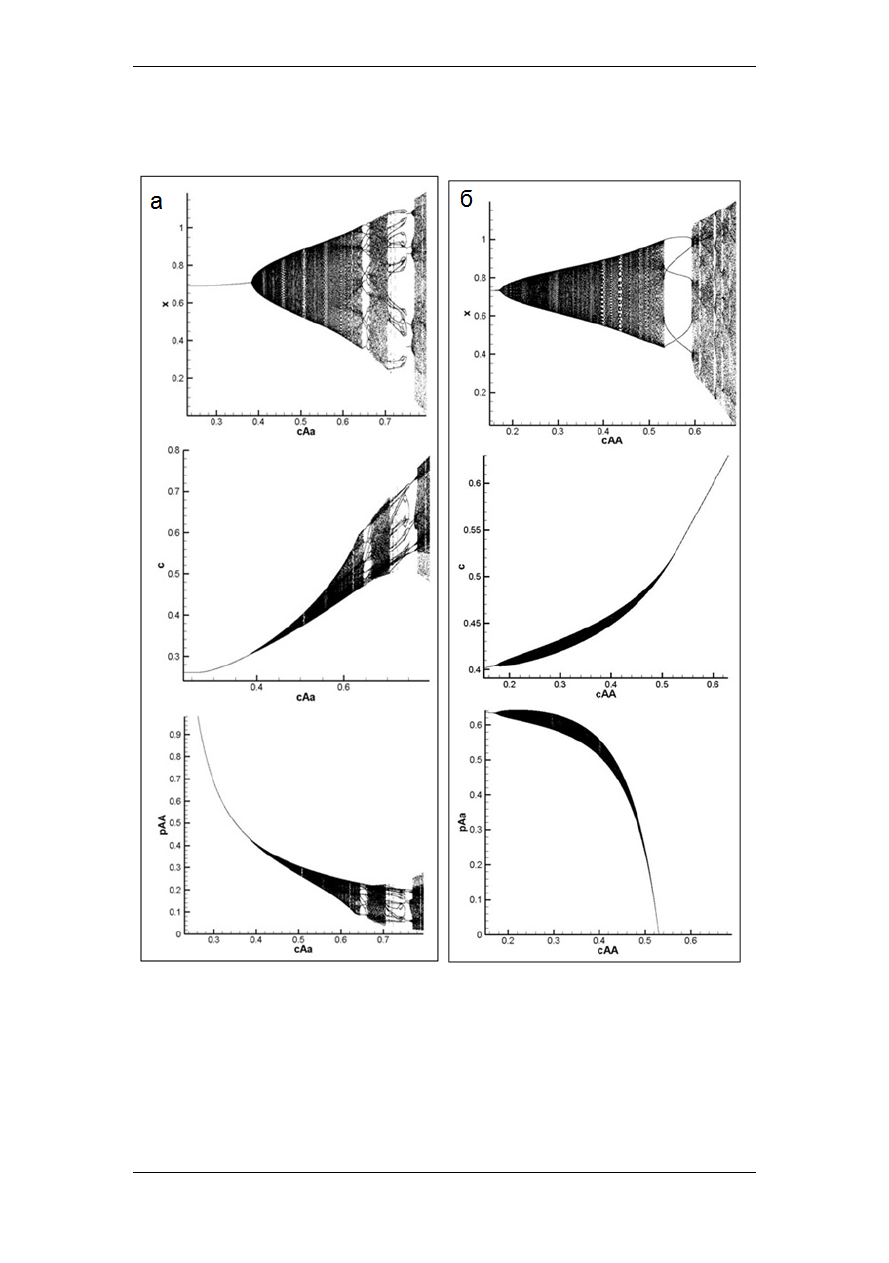
популяции, при этом генетический состав может флуктуировать (рис. 1а) или на-
оборот стабилизироваться (рис. 1б).
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
82
Рис. 1.
Распределение численности младшего возрастного класса (
x
), сред-
ней выживаемости (
¯
c
) и частоты генотипа (
AA
– (а) и
Aa
–(б)) репродук-
тивной группы в предельных траекториях системы (1) с изменением бифур-
кационного параметра
c
Aa
(а) и
c
AA
(б).
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
83
3.
Заключение
В работе рассматривается эволюция двухвозрастной популяции, при этом боль-
шее внимание уделяется моделированию механизмов наследования адаптивных по-
пуляционных характеристик. Разработана модель динамики генетической структу-
ры и численности для популяции с отбором по выживаемостям в репродуктивной
группе. Эта модель вместе с аналогом, где моделируется отбор по приспособленно-
стям зародышей, позволяет глубже понять эволюционные процессы, протекающие
в структурированной популяции. Проведенное исследование в целом подтверждает
результаты предыдущих исследований, которые изучали только динамику числен-
ности двухвозрастной популяции. Действительно, увеличение репродуктивного по-
тенциала w и выживаемости c сопровождается усложнением динамики численности
популяции. Однако эволюционный рост самих этих параметров может быть немо-
нотонным, со значительными флуктуациями. Рассматриваемые модели допускают
существенное разнообразие динамики генетической структуры двухвозрастной по-
пуляции. При этом увеличение средней выживаемости репродуктивной группы мо-
жет как дестабилизировать, так и привести к стабилизации динамики генетическо-
го состава популяции. Исследование проведено при частичной поддержке РФФИ
(грант №11-01-98512) и ДВО РАН в рамках программы Президиума РАН (проекты
№ 12-I-П28-02, 12-I-П15-02, 12-II-CO-06-019, 12-06-007, 13-III-В-01I-002).
Список литературы
1.
Базыкин А.Д. Математическая биофизика взаимодействующих популяций. М.: На-
ука, 1985.
2.
Волькенштейн М. В. Биофизика. М.: Наука, 1988.
3.
Романовский Ю.М., Степанова Н.В., Чернавский Д.С. Математическое моделирова-
ние в биофизике. Введение в теоретическую биофизику. Ижевск: Институт компью-
терных исследований, 2004.
4.
Rougharden J. Density dependent natural selection // Ecology. 1971. Vol. 52. P. 453-468.
5.
Charlesworth B. Selection in density-regulated populations // Ecology. 1971. Vol. 52. P.
469-474.
6.
Евдокимов Е.В. Проблемы регулярного поведения и детерминированного хаоса в
основных моделях популяционной динамики (Теория и эксперимент): автореферат
дис. д-ра. биол. наук. Красноярск, 1999.
7.
Фрисман Е.Я., Жданова О.Л., Колбина Е.А. Влияние промысла на генетическое
разнообразие и характер динамического поведения менделевской лимитированной
популяции // Генетика. 2010. Т. 46, № 2. С. 272-281.
8.
Leslie P.H. On the use of matrices in certain population mathematics // Biometrika. 1945.
Vol. 33. P. 183–212.
9.
Leslie P.H. Some further notes on the use of matrices in population mathematics //
Biometrika. 1948. Vol. 35. P. 213–245.
10.
Lefkovitch L.P. The study of population growth in organisms grouped by stages.
Biometrics. 1965. Vol. 21. P. 1–18.
11.
Свирежев Ю.М., Логофет Д.О. Устойчивость биологических сообществ. М.: Наука,
1978.
12.
Логофет Д.О. К теории матричных моделей динамики популяций с возрастной и
дополнительными структурами // Журнал общей биологии. 1991. Т. 52, № 6. С.
793-804.
13.
Логофет Д.О. Три источника и три составные части формализма популяции с дис-
кретной стадийной и возрастной структурами // Математическое моделирование.
2002. Т. 14, № 12. С. 11-22.
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
84
14.
Caswell H. Matrix population models: Construction, analysis and interpretation, 2nd
Edition. Sunderland, Massachusetts: Sinauer Associates, 2001.
15.
Логофет Д.О., Белова И.Н. Неотрицательные матрицы как инструмент моделирова-
ния динамики популяций: классические модели и современные обобщения // Фун-
даментальная и прикладная математика. 2007. Т. 13., №4. С. 145-164.
16.
Hastings A. Age dependent dispersal is not a simple process: density dependence, sta-
bility and chaos // Theoretical Population Biology. 1992. Vol. 41, № 3. P. 388–400.
17.
Lebreton J.D. Demographic models for subdivided populations: the renewal equation
approach // Theoretical Population Biology. 1996. Vol. 49, № 3. P. 291–313.
18.
Kooi B.W., Kooijman S.A.L.M. Discrete event versus continuous approach to
reproduction in structured populations dynamics // Theoretical Population Biology. 1999.
Vol. 56, № 1. P. 91–105.
19.
Жданова О.Л., Фрисман Е.Я. Нелинейная динамика численности популяции: вли-
яние усложнения возрастной структуры на сценарии перехода к хаосу // Журнал
общей биологии. 2011. T. 72, №3. С. 214–228.
20.
Фрисман Е.Я, Скалецкая Е.И. Странные аттракторы в простейших моделях дина-
мики численности биологических популяций // Обозрение прикладной и промыш-
ленной математики. 1994. Т. 1., Вып. 6. С. 988–1008.
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.