Файл: Тема Общие вопросы реализации программы по математике в начальных классах.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 380
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2. Раздели на число каждое слагаемое, а потом сложи полученные результаты: (6+9):3=6:3+9:3=2+3=5.
3. Сравни результаты.
Новый способ действия закрепляется в процессе выполнения упражнений: Вычисти значение каждого выражения двумя способами: (10+4):2, (8+12):4, (12+15):3.
Для знакомства учащихся со свойством деления суммы на число использован другой методический подход.
Предлагается такое задание:
Догадайся! По какому правилу записаны выражения в каждом столбике?
Вычисли их значения: 54:9 (36+18):9 36:9+18:9; 63:7 (49+14):7 49:7+14:7.
В процессе выполнения этого задания, учащиеся осознают новый способ действия. А именно: делимое представляется в виде суммы двух слагаемых, каждое из которых делится на данное число, затем на это число делится каждое слагаемое и полученные результаты складываются. Для усвоения нового способа действия выполняются различные задания. При этом выражения, используемые в заданиях, включают только табличные случаи деления, поэтому учащиеся не испытывают затруднений в применении нового способа действия.
23. Методика знакомства со свойством умножения числа на сумму: методика знакомства со свойством (1 способ); методика знакомства со свойством (2 способ).
[См. билет 21]
Возможно имелась в виду умножение числа на разность. Вводится она по аналогии со сложением.
24. Взаимосвязь компонентов при умножении и делении: взаимосвязь компонентов при умножении; взаимосвязь компонентов при делении.
В 3 классе дети знакомятся с правилом взаимосвязи компонентов умножения, которое является основой для обучения нахождению неизвестных компонентов умножения при решении уравнений если произведение разделить на один множитель, то получится другой множитель. правило проверки действия умножения:
1. произведение делят на множитель.
2. сравнивают полученный результат с другим множителем. Если эти числа равны, умножение выполнено верно. 18*4=72. Проверка:1) 72:4=18; 2) 18=18
Компоненты умножения – 1 множитель, 2 множитель, произведение
Правила.
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Компоненты деления – делимое, делитель, частное.
Правила.
Чтобы найти неизвестное делимое надо делитель умножить на частное.
Чтобы найти неизвестный делитель, надо делимое разделить на частное.
Тема 8. Теоретические и методические основы обучению решения задач.
1. Текстовая задача и процесс ее решения. Понятие текстовой задачи, ее структура. Методы и способы решения текстовых задач. Основные этапы решения задачи (анализ, поиск плана, его выполнение, проверка) и приемы выполнения этих этапов. Моделирование в процессе решения задачи.
Текстовая задача – описание некоторой ситуации на естественном языке, с требованием дать количественную характеристику какого-либо компонента этой ситуации, установить наличие или отсутствие некоторого отношения между её компонентами и определить вид этого отношения.
Структура: условие, вопрос, решение, ответ.
Основными методами решения текстовых задач являются арифметический и алгебраический.
Решить задачу арифметическим методом – это значит найти ответ на требование задачи посредством выполнения арифметических действий над числами.
Решить задачу алгебраическим методом – это значит найти ответ на требование задачи, составив и решив уравнение или систему уравнений.
Этапы решения:
1. Анализ задачи.
2. Поиск плана решения задачи.
3. Осуществление плана решения задачи.
4. Проверка решения задачи.
Анализ задачи:
Приемы:
1. Разобраться в содержании задачи, вычленить условия и требования можно, если задать специальные вопросы и ответить на них.
2. Большую помощь в осмыслении задачи оказывает другой прием – перефразировка текста задачи.
Поиск плана решения задачи: установить связь между данными и искомыми объектами, наметить последовательность действий.
Наиболее популярный приём - разбор задачи по тексту или по ее вспомогательной модели.
Разбор задачи проводится в виде цепочки рассуждений, которая может начинаться как от данных задачи, так и от ее вопросов.
Осуществление плана решения задачи: найти ответ на требование задачи, выполнив все действия в соответствии с планом: запись по действиям (с пояснением, без пояснения, с вопросами) и запись в виде выражения.
Проверка решения задачи: установить правильность или ошибочность выполненного решения.
Приемы:
1. Установление соответствия между результатом и условиями задачи.
2. Решение задачи другим способом.
Моделирование в процессе решения задачи
Математической моделью текстовой задачи является выражение (либо запись по действиям), если задача решается арифметическим методом, и уравнение (либо система уравнений), если задача решается алгебраическим методом.
В процессе решения задачи четко выделяются три этапа математического моделирования:
1 этап – это перевод условий задачи на математический язык;
2 этап – внутримодельное решение;
3 этап – интерпретация.
Наибольшую сложность в процессе решения текстовой задачи представляет перевод текста с естественного языка на математический
Схематизированные модели, в свою очередь, делятся на вещественные и графические в зависимости от того, какое действие они обеспечивают.
Графические модели используются, как правило, для обобщенного, схематического воссоздания ситуации задачи. К графическим следует отнести следующие виды моделей:
1. рисунок;
2. условный рисунок;
3. чертеж;
4. схематичный чертеж (или просто схема).
2. Подготовительная работа к ознакомлению с понятием задача: цель работы в этот период; ориентир для составления рассказов; примеры рассказов по одной картинке.
Цель работы в данный период: формирование у учащихся основных познавательных действий, представлений о ключевых отношениях мира:
- отношение целого и части
- равенствах и неравенствах
-
 числа и действия над ними
числа и действия над ними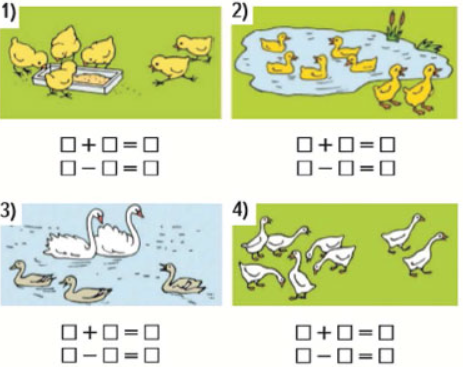
3. Первое знакомство с задачей: отличие задачи от других заданий; знакомство с задачей и ее частями; примеры текстовых задач, которые полезно рассмотреть на уроке; использование средств наглядности.
Отличие задачи от других заданий – понимание сути и описание явление, по которому следует решение.
На этой ступени обучения решению задач того или другого вида должна быть создана у учащихся готовность к выбору арифметических действий при решении соответствующих задач: они должны усвоить знание тех связей, на основе которых выбираются арифметические действия, знание объектов и жизненных ситуаций, о которых говорится в задачах.
До решения простых задач ученики усваивают знание следующих связей:
1. Связи операций над множествами с арифметическими действиями, то есть конкретный смысл арифметических действий.
2. Связи отношений «больше» и «меньше» (на сколько единиц и в несколько раз) с арифметическими действиями
3. Связи между компонентами и результатами арифметических действий, то есть правила нахождения одного из компонентов арифметических действий по известному результату и другому компоненту.
4. Связи между данными величинами, находящихся в прямо или обратно пропорциональной зависимости, и соответствующими арифметическими действиями.
Первое знакомство с задачей строится на простейших задачах (на нахождение суммы и остатка) с использованием неполной предметной наглядности, с тем, чтобы ответ на вопросы задачи не был очевиден для детей.
Особенно труден для учащихся первый этап — анализ текста задачи. Поэтому необходимо с самого начала обучения решению задач формировать у младших школьников общее умение анализировать задачи. Для этого учитель сначала читает задачу, знакомит детей с её 4 частями: условие, вопрос, решение, ответ.
При решении задачи в два и более действий, решающее значение имеет умение найти и составить план решения задачи. С этой целью используют рассуждения от данных к искомым величинам (синтетический) и, наоборот, от искомых (вопроса задачи) к данным (известным) величинам (аналитический), возможна их комбинация (аналитико- синтетический способ рассуждений).
4. Основные этапы работы над задачей: ознакомление с содержанием задачи; поиск решения задачи; способы разбора задач; выполнение решения(формы записи); проверка решения (способ подстановки, прикидка, решение задачи другим способом, составление и решение обратной задачи).
Этапы работы над задачей:
1. Ознакомление с содержанием задачи
2. поиск решения задачи
3. способы разбора задач
4. выполнение решения задачи
5. проверка решения задачи
1. Ознакомление с содержанием задачи
Ознакомиться с содержанием задачи – это не только прочитать её, важно представить то, о чём говорится в условии, ту жизненную ситуацию, которая отражена в задаче. Важно при чтении задачи уметь определить процесс, который описывается в условии, который помогает определить выбор действий. При выборе действий помогают слова: «было», «продали», «убрали», «часть», «осталось», «разделили на…», «стало поровну». Читая задачу, важно «видеть» и выделять интонацией вопрос задачи. Если в условии задачи встречаются трудные или непонятные слова, то над их значением надо поработать.
2. Поиск решения задачи
Очень важно, чтобы ученики научились выделять в задаче величины, данные и искомые числа, умели устанавливать связи между данными и искомыми и, только после этого у них получится выбрать правильные арифметические действия.
В поиске решения задачи используются различные приёмы. Одним из самых распространённых приёмов является иллюстрирование.
Иллюстрация задачи – это использование средств наглядности для нахождения величин задачи, данных и искомых чисел, а также для установления связей между ними. Иллюстрации могут быть предметными или схематичными. Предметные иллюстрации помогают ярко представить те жизненные ситуации, которые описываются в задаче.
Начиная с 1 класса учащиеся знакомятся со схематическими иллюстрациями, при помощи которых устанавливаются связи между данными и искомыми с помощью схем, отрезков, стрелок и других графических изображений.
3. Способы разбора задач
На основе аналитического и синтетического методов решения задач при работе над поиском решения задачи применяются два основных способа разбора задачи: аналитический (анализ) и синтетический (синтез). Однако на практике чаще употребляют аналитическо-синтетический разбор задачи.
Под анализом подразумевают способ рассуждений от общего к частному (анализировать – разбивать на составляющие)
Под синтезом подразумевают способ рассуждений от частного к общему (синтезировать – получать из частей).
4. Выполнение решения задачи
Выполнение арифметических действий, которые выбраны при составлении плана решения – это и есть решение задачи.
Важно обращать внимание на пояснение, которое пишет ученик.
В начальной школе используются основные формы записи решения:
- выражение и нахождение его значения;
- запись по действиям с пояснением.
5. Проверка решения задачи
Проверка решения задачи нужна для того, чтобы установить правильное решение или нет.
Чтобы проверить правильность решения, можно:
1. Подстановка.
2. Прикидка ответа
3. Решить задачу другим способом.
4. Составить и решить обратную задачу.
5. Разбор задачи (аналитический, синтетический): аналитический способ разбора задачи; синтетический способ разбора.
На основе аналитического и синтетического методов решения задач при работе над поиском решения задачи применяются два основных способа разбора задачи: