Кроме того для предикатов определяют ещё две операции:

• 
  Квантор общности 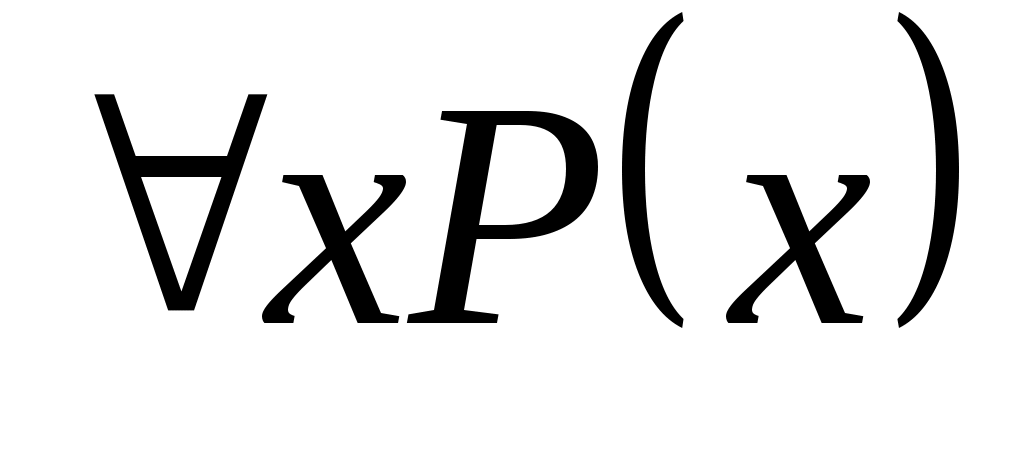- читают: «для всех x имеет место 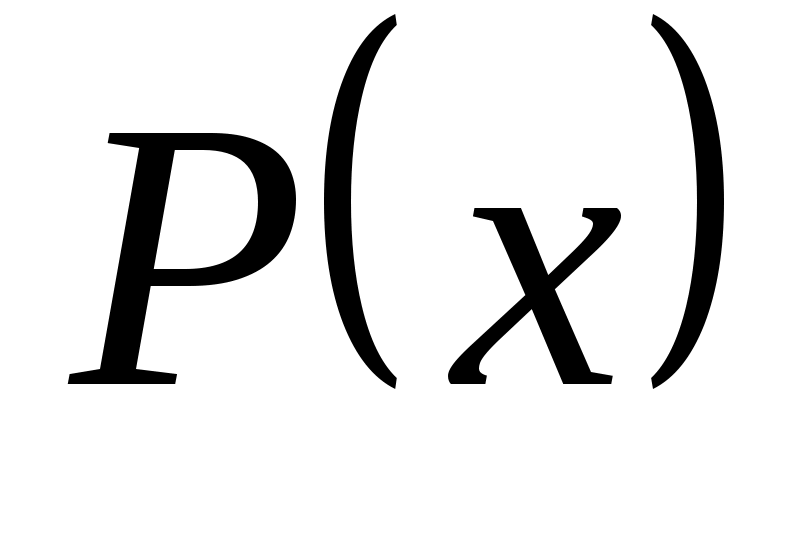» (или «для любого x имеет место 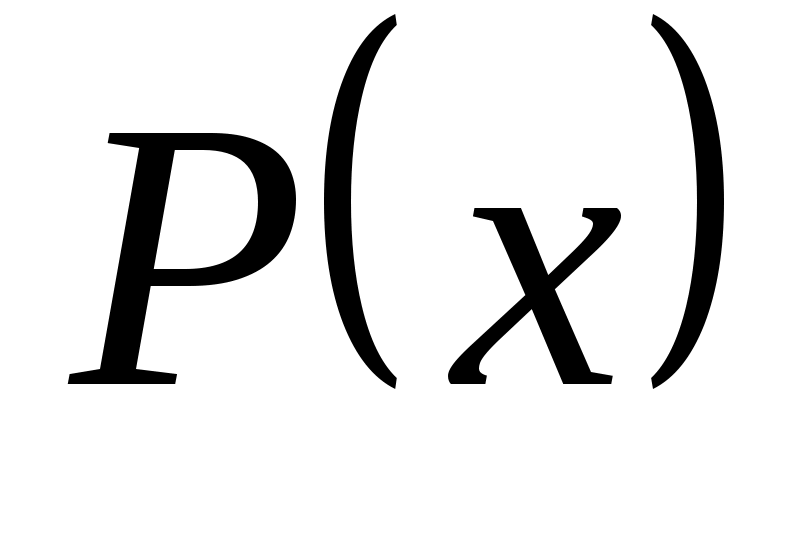», «для каждого x имеет место »)
  
• 
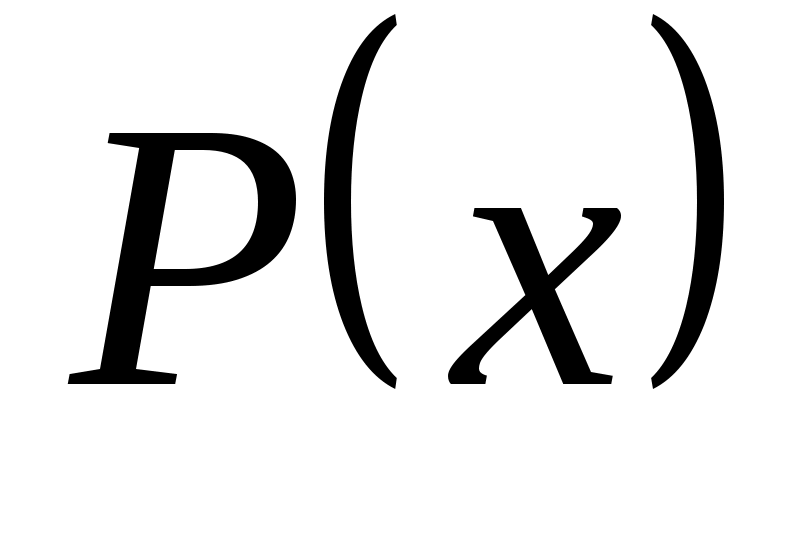  Квантор существования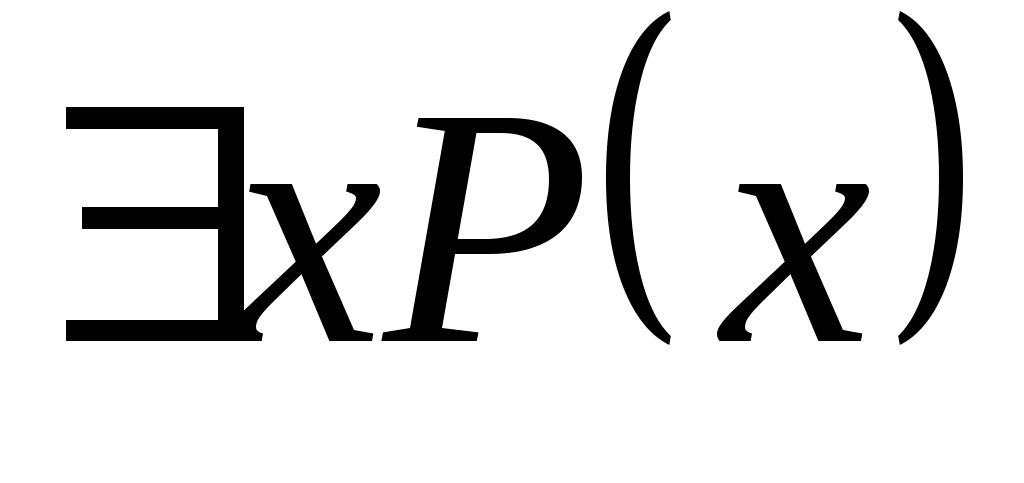 - читают: «существует x, для которого имеет место 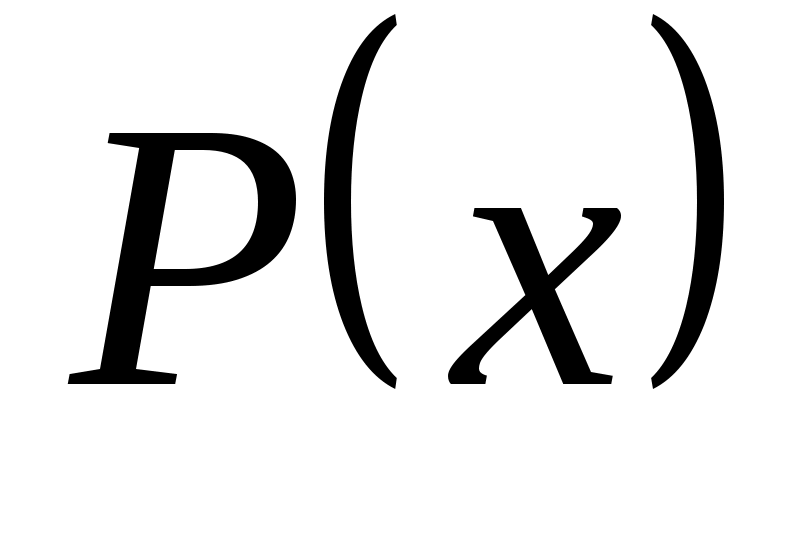» (или «найдётся x, для которого имеет место »)
  

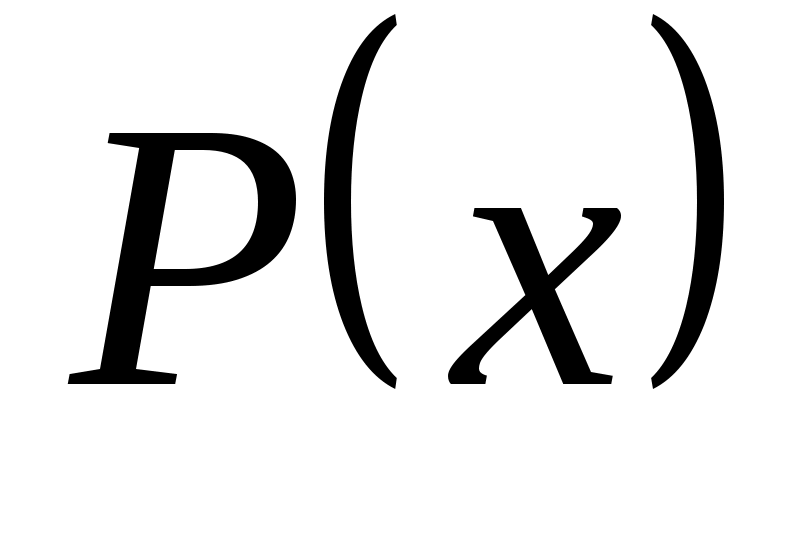Эти операции применяются к одному предикату, они ставят в соответствие одноместному предикату - высказывания и , логические значения которых определяются так:

=

=
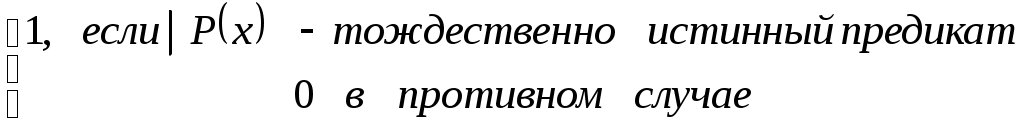
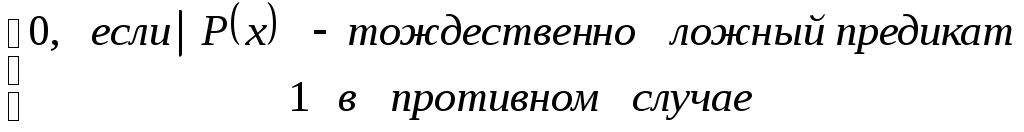
Кванторы можно применять к n-местному предикату, в результате получают (n-1)-местный предикат.

Переменную, к которой относится квантор называют связанной, остальные переменные называют свободными.
3. Формулы логики предикатов.
Применяя к предикатам операции отрицания, конъюнкции, дизъюнкции, импликации, эквивалентности, квантор общности, квантор существования, получаем формулы логики предикатов.

Примеры: 1.

---

2.

Формула логики предикатов называется тавтологией, если приподстановке любых конкретных предикатов она всегда обращается в тождественно-истинный предикат.

Сформулируем следующие правила:

1. 
   Формула логики предикатов называется атомарной (элементарной), если в ней нет связанных переменных.
   
2. 
   Если F- формула, то и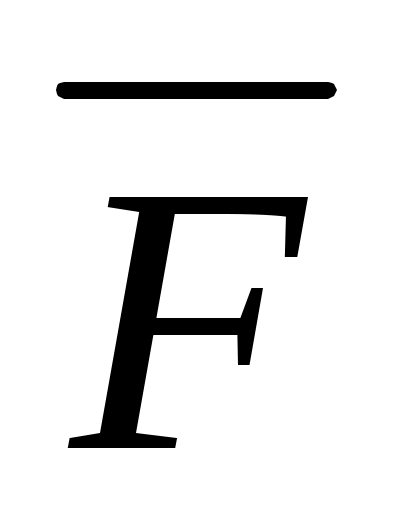 - тоже формула. Свободные и связанные переменные формулы F так же являются свободными и связанными переменными в формуле .
   
3. 
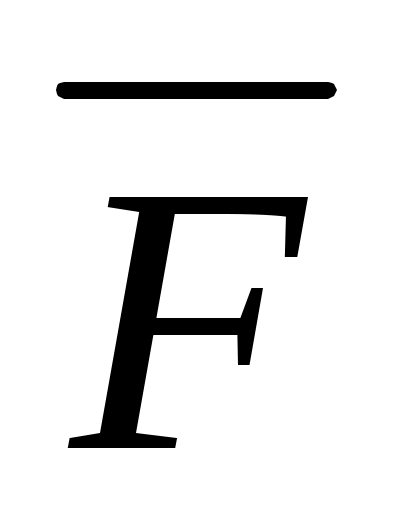   ПустьF и G– формулы, и в них нет переменных, которые были бы связаны в одной и свободны в другой формуле. Тогда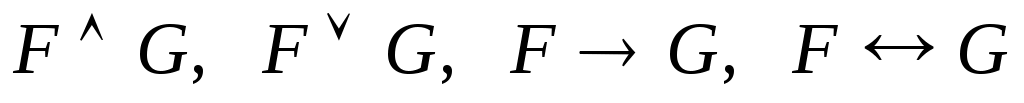 - формулы, в которых свободные переменные формул FиG остаются свободными, а связанные – связанными.
   
4. 
   Пусть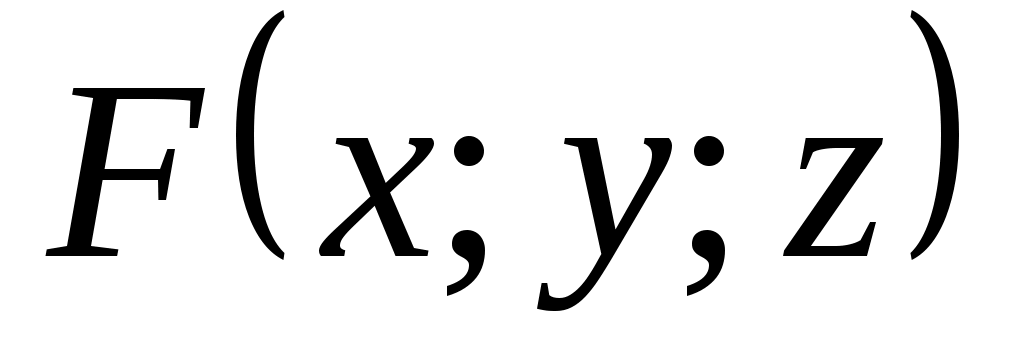 - формула, содержащая свободные переменные x, y, z. Тогда 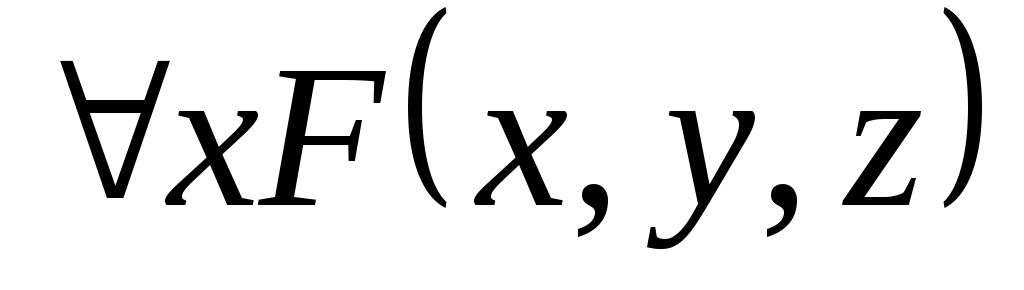и 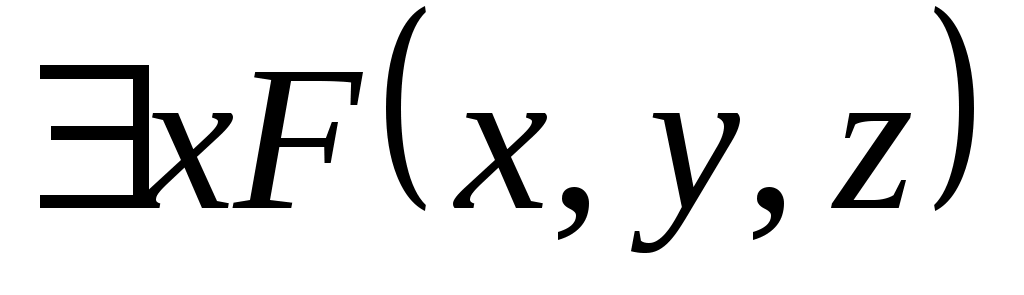- формулы, в которых переменная x – связанная, а остальные свободные.
   

4. Равносильные формулы логики предикатов.
Формулы F и Gравносильны в логике предикатов, если они равносильны на всех множествах. При этом пишут .

Рассмотрим равносильные формулы логики предикатов:

1. 
   
   

- перенос квантора через отрицание

---

2.

- вынос квантора за скобки





3.

- перестановка одноимённых

кванторов
Примеры:

1. 
   Переведите следующие высказывания на язык алгебры предикатов:
   

а) все целые числа неотрицательны

Решение:

б) хотя бы одно натуральное число делится на 6

Решение:

2. 
   Пусть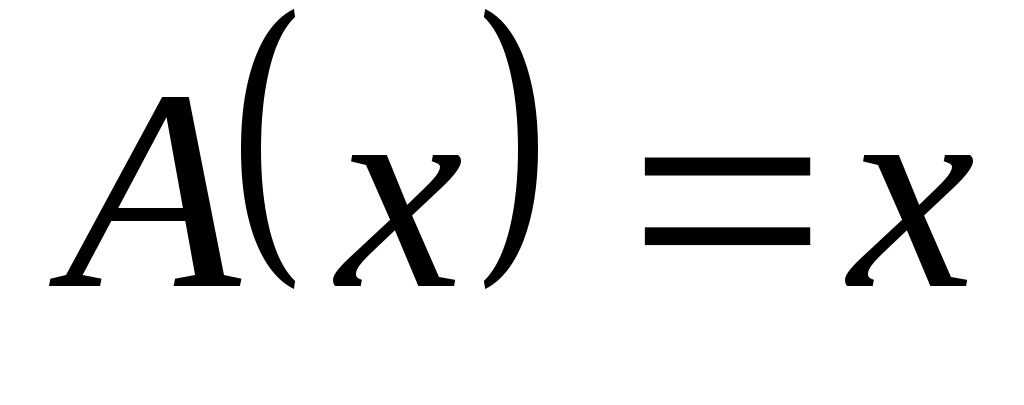 – составное число, 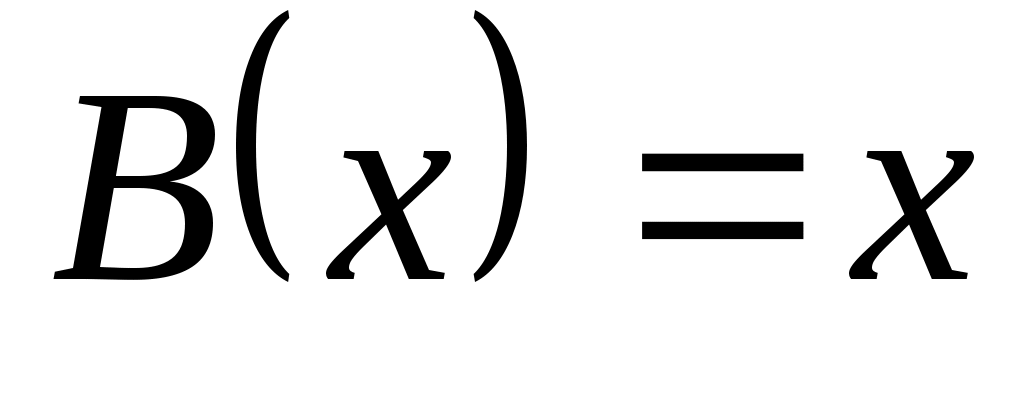- чётное число. Переведите на русский язык следующие символические записи на языке алгебры предикатов:
   

а)

Решение: Найдётся целое число либо составное, либо чётное.

б)

Решение: Если любое рациональное число составное, то оно нечётное.

3. Пусть , переведите на русский язык следующую символическую запись на языке алгебры предикатов

Решение: Для любого натурального числа x найдётся целое число y такое, что их сумма будет отрицательной.

III. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО НАПИСАНИЮ И ОФОРМЛЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
1. Общие положения
Основная форма изучения программного материала для обучающихся заочного отделения – это самостоятельная работа. Одной из форм работы при обучении, а также способом осуществления контроля является выполнение контрольных заданий в межсессионный период.

---

Обучающимся заочного отделения предлагается контрольная работа по дисциплине «Элементы математической логики».

Выполненная контрольная работа должна быть в установленные колледжем сроки представлена на заочное отделение колледжа для регистрации и проверки преподавателем.

Не зачтенная контрольная работа должна быть выполнена повторно с учетом указанных замечаний и вновь представлена на заочное отделение колледжа для регистрации и проверки.

2. Методические указания по оформлению контрольной работы
Являясь формой итогового контроля, письменная работа позволяет оценить уровень подготовки автора работы, умение самостоятельно анализировать и использовать различные источники, в том числе и интернет-ресурс.

Предлагаемые контрольные задания составлены в соответствии с учебной программой, актуальности проблем, имеющих место в изучаемой дисциплине.

Цель работы – самостоятельное закрепление теоретических знаний и получение практических навыков по учебной дисциплине.

Выполнение контрольной работы позволяет каждому обучающемуся проявить самостоятельность и творческое отношение к учебному процессу.

Для изучения материала и выполнения контрольной работы могут быть использованы: учебники, учебные пособия, научные издания, ресурсы сети «Интернет» и другой материал.

Контрольное задание должно быть выполнено в полном объеме и в полном соответствии с предложенным перечнем варианта. Не разрешается в контрольной работе выполнять задание из разных вариантов.

При выполнении контрольной работы обучающемуся необходимо руководствоваться следующим:

1. Контрольная работа выполняется самостоятельно. Замена контрольной работы другой, взятой из аналогичного пособия или другой вариант - не допускаются.

2. Номер варианта контрольных заданий соответствует номеру студента по учебному журналу.

3. Контрольная работа выполняется в обычной школьной тетради, на лицевой стороне которой (на обложке) приводятся сведения по следующему образцу ( смотри приложение)

4. Условия задач переписываются полностью без сокращений. Для замечаний преподавателя на страницах тетради оставляются поля. Задачи выполняются по порядку их расположения в Вашем варианте.

5. Решения задач должны сопровождаться исчерпывающими, но краткими объяснениями, раскрывающими ход и методы решения задач.

---

6. В конце контрольной работы необходимо указать, каким учебником или учебным пособием студент пользовался при изучении математической логики (название учебника , автор, год издания).

7. Контрольная работа передаётся ведущему преподавателю во время экзаменационной сессии.

3. Варианты контрольных работ
КОНТРОЛЬНАЯ РАБОТА

ПО ЭЛЕМЕНТАМ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
Вариант 1

1. 
   Найдите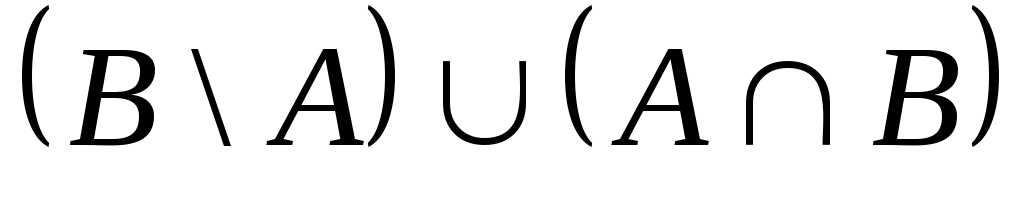 , если , .
   
2. 
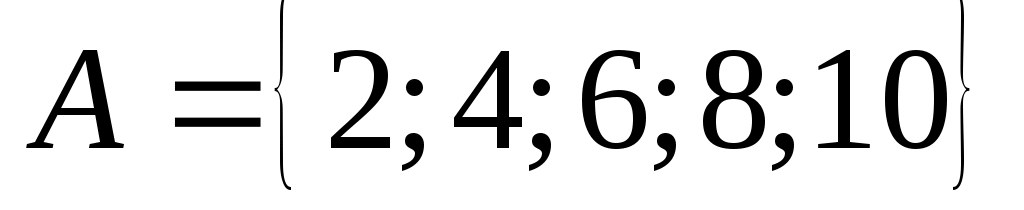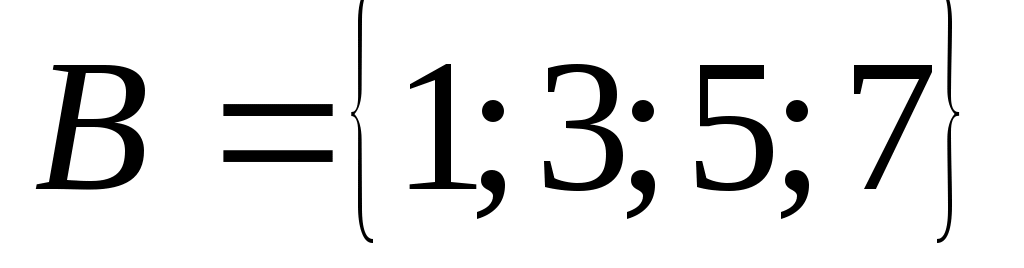   Является ли предложение «Магазин закрыт на обед» высказыванием. Почему?
   
3. 
   Определите значение истинности высказывания «Если Сахара - пустыня, то Африка - остров».
   
4. 
   Составьте таблицу истинности .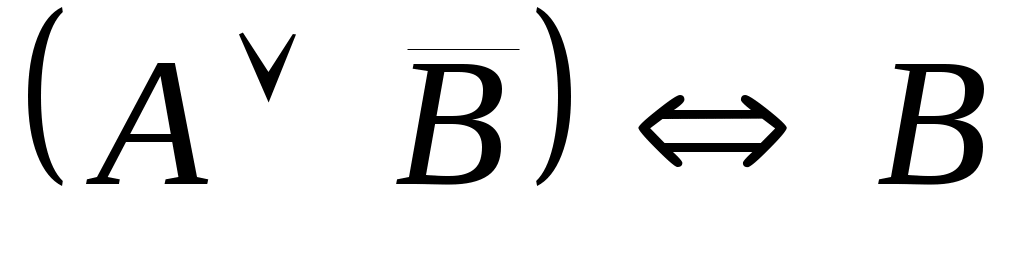
   
5. 
   Упростите формулу: .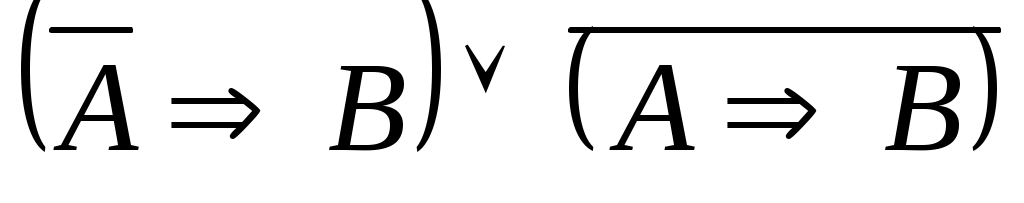
   
6. 
   Равносильными преобразованиями приведите формулу к СДНФ: .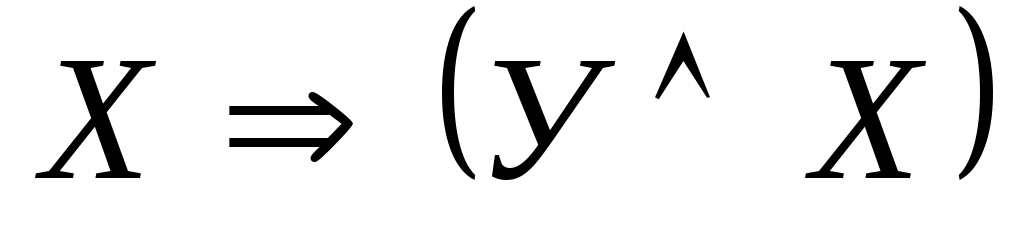
   
7. 
   Постройте таблицу значений булевой функции: .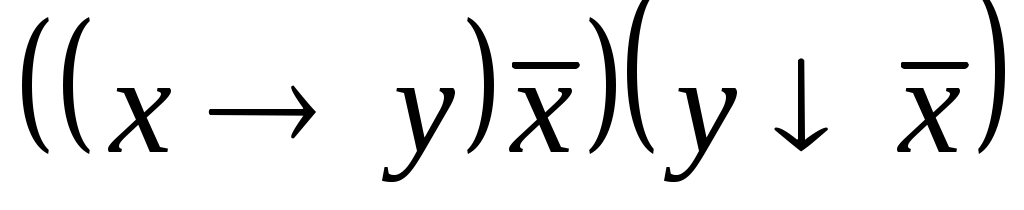
   
8. 
   Решите булево уравнение: .
   
9. 
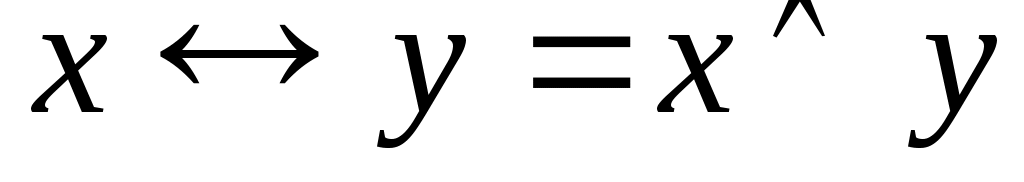   Найдите область истинности предикатов: , , , .
   
10. 
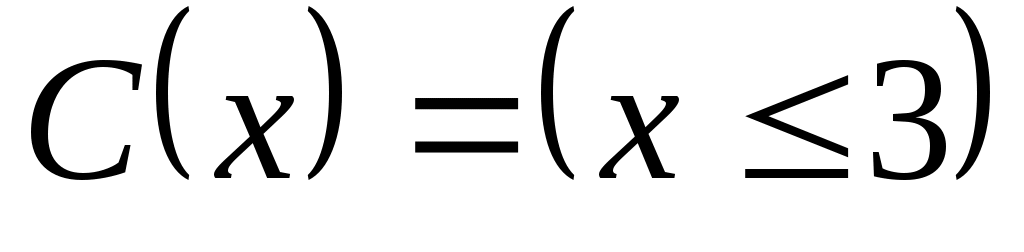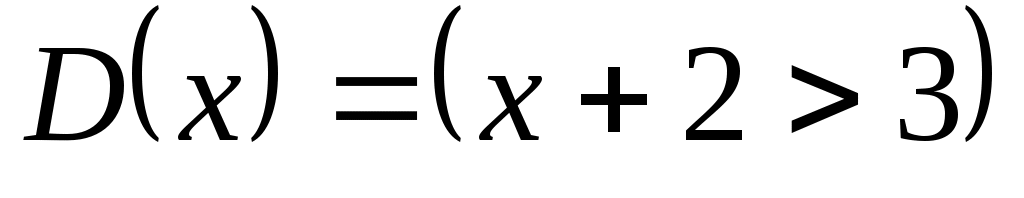    Пусть А(х) = (х – составное число), В(х) = (х – четное число). Переведите на русский язык символическую запись на языке алгебры предикатов: .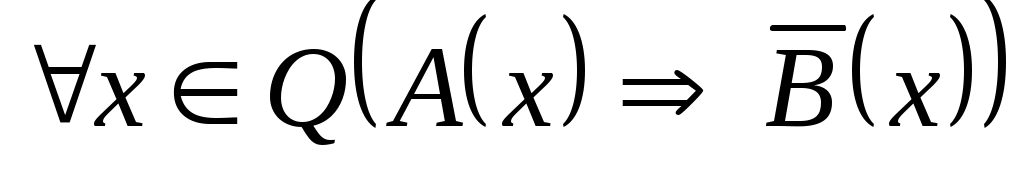
    

---

Смотрите также файлы

• Бизнесплан предпринимательского проекта открытие магазина косметических средств.docx

• В человеке рядом с философией присутствуют и другие деятельности.docx

• Практических заданий по дисциплине психокоррекция.docx

• Правила посадки в автобус.docx

• Занятие (2 часа).docx