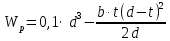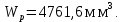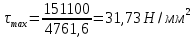Файл: белорусский государственный технологический университет.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 60
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
6. Проверочные расчеты ведомого вала редуктора и его подшипников
Построим схему нагружения валов согласно схеме для редукторов, изображенной на с. 136 [1]:
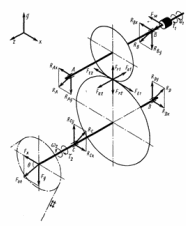
Рисунок 6.1 – Схема нагружения валов
По правилам сопротивления материалов, рассматривая вал как балку, лежащую на шарнирно-подвижных опорах и нагруженную сосредоточенными силами, определяем реакции в опорах в горизонтальной и вертикальной плоскостях и строим эпюры изгибающих моментов (рис. 6.2).
Колесо косозубой цилиндрической передачи симметрично относительно подшипниковых опор, а коническая шестерня открытой передачи расположена на конце консольного участка ведомого вала редуктора.
В нашем случае имеем:
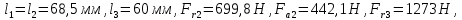
Fa3 = 380 H.
Вертикальная плоскость
Определим реакции опор.
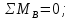RAy*(l1 + l2) - Fr2*l2 – Fa2*d2/2 = 0,
RAy*(l1 + l2) - Fr2*l2 – Fa2*d2/2 = - RA·(68,5 + 68,5) – 699,8·68,5 – 442,1*165,2/2 = RA·137 – 84436,3 = 0,
RAy = 84436,3/137 = 616,3 Н;
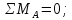- RBy*(l1 + l2) + Fr2*l1 – Fa2*d2/2 = 0,
- RBy(l1 + l2) – Fr2*l1 – Fa2*d2/2 = - RBy·(68,5 + 68,5) + 699,8·68,5 – 36,5 =
= - RBy·137 + 11436,3 = 0,
RBy = 11436,3/137 = 83,5 Н;
Проверка:
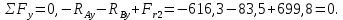
Реакции определены правильно.
Строим эпюру изгибающих моментов.
Участок I (0 ≤ z ≤ 68,5):
MI(z) = - RA*z = - 616,3z;
Значения M на краях отрезка:
MI(0) = - 616,3·0 = 0;
MI(68,5) = - 616,3·68,5 = - 42,2 Н*м;
Участок II (68,5 ≤ z ≤ 137):
MII(z) = - RA*z + F1(z - c1) + Fa2*
d2/2 = - 616,3z + 699,8(z – 68,5) + 36,5 =
= 83,5z - 0.011436;
Значения M на краях отрезка:
MII(0.0685) = 83,5·0,068,5 - 11,436 = - 5,72 Н*м;
MII(0.137) = 83,5·0,137 – 11,436 = 0.
Участок III (137<Z<197)
На этом участке в данной плоскости внешние нагрузки отсутствуют, поэтому изгибающий момент равен нулю.
Горизонтальня плоскость
Определим реакции опор.
RAx*(l1 + l2) - Fr3*l3 – Fa3*d3/2 = 0,
RAx*(l1 + l2) - Fr3*l2 – Fa3*d3/2 = RAx·(68,5 + 68,5) – 1273·60 – 380*82,34/2 = RA·137 – 91980,3 = 0,
RAx = 91980,3/137 = 671,4 Н;
RBx*(l1 + l2) - Fr3*L – Fa3*d3/2 = 0,
RBx(l1 + l2) – Fr3*L – Fa3*d3/2 = RBx·(68,5 + 68,5) - 1273·197 – 36,5 =
= - RBx·137 + 266381 = 0,
RBx = 266381/137 = 1944,4 Н;
Проверка:
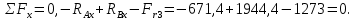
Реакции определены правильно.
Строим эпюру изгибающих моментов.
Участок I (0 ≤ z ≤ 0.137):
Изгибающий момент M:
MI(z) = - RA z = - 671,7z;
Значения M на краях отрезка:
MI(0) = - 671,7·0 = 0;
MI(0,137) = - 671,7·0,137 = - 92 Н*м;
Участок II (0.137 ≤ z ≤ 0.197):
Изгибающий момент M:
MII(z) = - RA*z + RB(z – l1 - l2) = - 671,4z + 1944,4(z – 0,137) =
= 1273z – 266,38;
Значения M на краях отрезка:
MII(0,137) = 1273·0,137 – 266,38 = 92 Н*м;
MII(0,197) = 1273·0,197 – 266,38 = - 15,6 Н*м.
По результатам расчетов построены эпюры изгибающих моментов (рис. 6.2).
Определим суммарные моменты и реакции опор на валу 
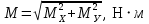
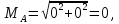
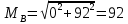
H∙м/
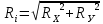
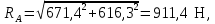
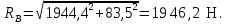
RBx
A B C z
RAx Fa3 Fr3
x RAy Fa2 Fr2 RBy
l1 l2 l3
Вертикальная плоскость
- 5,7
-42,2
Горизонтальная плоскость
-15,6
- 92
Результирующая эпюра
-15,6
62,4
92
Рисунок 6.2 – Эпюры изгибающих моментов
Проверочный расчет вала на прочность проводим при совместном действии изгиба и кручения путем определения коэффициентов запаса прочности в опасных сечениях и сравнении их с допускаемыми.
Как видно из эпюр, опасное сечение возникает в опоре В. Момент в этом сечении равен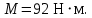
Коэффициент запаса прочности определяется по формуле:
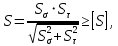
где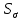
- коэффициент запаса по изгибным напряжениям;
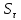- коэффициент запаса по крутящим напряжениям;
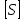- допускаемое значение коэффициент запаса,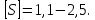 
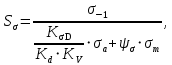
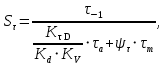
где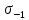
- предел выносливости для материала вала при симметричном изгибе
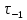- предел выносливости для материала вала при симметричном изгибе;
, 
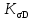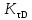- эффективные коэффициенты концентрации напряжений;
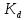- коэффициент влияния абсолютных размеров поперечного сечения;
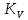- коэффициент влияния поверхностного упрочнения;
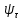- коэффициент чувствительности к асимметрии цикла напряжений;
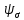- коэффициент чувствительности к асимметрии цикла напряжений;
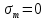- среднее напряжение цикла;
;
;
;
; .
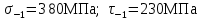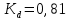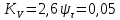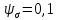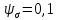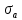- амплитудное напряжение цикла, определяемое по формуле:
,
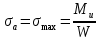где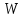
- осевой момент сопротивления сечения вала, определяемый:
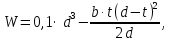
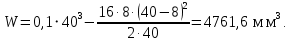
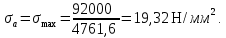
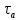- амплитудное напряжение;
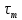- среднее напряжение цикла, определяемое по формуле:
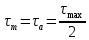
где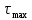
- максимальное напряжение, определяемое по формуле:
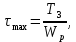
где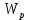
- полярный момент сопротивления сечения вала, определяемый по:
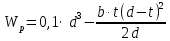
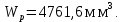
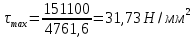
Построим схему нагружения валов согласно схеме для редукторов, изображенной на с. 136 [1]:
Рисунок 6.1 – Схема нагружения валов
По правилам сопротивления материалов, рассматривая вал как балку, лежащую на шарнирно-подвижных опорах и нагруженную сосредоточенными силами, определяем реакции в опорах в горизонтальной и вертикальной плоскостях и строим эпюры изгибающих моментов (рис. 6.2).
Колесо косозубой цилиндрической передачи симметрично относительно подшипниковых опор, а коническая шестерня открытой передачи расположена на конце консольного участка ведомого вала редуктора.
В нашем случае имеем:
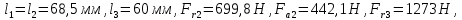
Fa3 = 380 H.
Вертикальная плоскостьОпределим реакции опор.
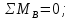RAy*(l1 + l2) - Fr2*l2 – Fa2*d2/2 = 0,RAy*(l1 + l2) - Fr2*l2 – Fa2*d2/2 = - RA·(68,5 + 68,5) – 699,8·68,5 – 442,1*165,2/2 = RA·137 – 84436,3 = 0,
RAy = 84436,3/137 = 616,3 Н;
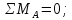- RBy*(l1 + l2) + Fr2*l1 – Fa2*d2/2 = 0,- RBy(l1 + l2) – Fr2*l1 – Fa2*d2/2 = - RBy·(68,5 + 68,5) + 699,8·68,5 – 36,5 =
= - RBy·137 + 11436,3 = 0,
RBy = 11436,3/137 = 83,5 Н;
Проверка:
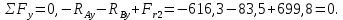
Реакции определены правильно.
Строим эпюру изгибающих моментов.
Участок I (0 ≤ z ≤ 68,5):
MI(z) = - RA*z = - 616,3z;
Значения M на краях отрезка:
MI(0) = - 616,3·0 = 0;
MI(68,5) = - 616,3·68,5 = - 42,2 Н*м;
Участок II (68,5 ≤ z ≤ 137):
MII(z) = - RA*z + F1(z - c1) + Fa2*
d2/2 = - 616,3z + 699,8(z – 68,5) + 36,5 =
= 83,5z - 0.011436;
Значения M на краях отрезка:
MII(0.0685) = 83,5·0,068,5 - 11,436 = - 5,72 Н*м;
MII(0.137) = 83,5·0,137 – 11,436 = 0.
Участок III (137<Z<197)
На этом участке в данной плоскости внешние нагрузки отсутствуют, поэтому изгибающий момент равен нулю.
Горизонтальня плоскость
Определим реакции опор.
RAx*(l1 + l2) - Fr3*l3 – Fa3*d3/2 = 0,RAx*(l1 + l2) - Fr3*l2 – Fa3*d3/2 = RAx·(68,5 + 68,5) – 1273·60 – 380*82,34/2 = RA·137 – 91980,3 = 0,
RAx = 91980,3/137 = 671,4 Н;
RBx*(l1 + l2) - Fr3*L – Fa3*d3/2 = 0,RBx(l1 + l2) – Fr3*L – Fa3*d3/2 = RBx·(68,5 + 68,5) - 1273·197 – 36,5 =
= - RBx·137 + 266381 = 0,
RBx = 266381/137 = 1944,4 Н;
Проверка:
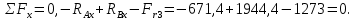
Реакции определены правильно.
Строим эпюру изгибающих моментов.
Участок I (0 ≤ z ≤ 0.137):
Изгибающий момент M:
MI(z) = - RA z = - 671,7z;
Значения M на краях отрезка:
MI(0) = - 671,7·0 = 0;
MI(0,137) = - 671,7·0,137 = - 92 Н*м;
Участок II (0.137 ≤ z ≤ 0.197):
Изгибающий момент M:
MII(z) = - RA*z + RB(z – l1 - l2) = - 671,4z + 1944,4(z – 0,137) =
= 1273z – 266,38;
Значения M на краях отрезка:
MII(0,137) = 1273·0,137 – 266,38 = 92 Н*м;
MII(0,197) = 1273·0,197 – 266,38 = - 15,6 Н*м.
По результатам расчетов построены эпюры изгибающих моментов (рис. 6.2).
Определим суммарные моменты и реакции опор на валу
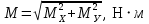
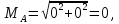
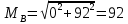
H∙м/
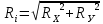
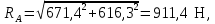
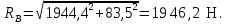
RBx A B C z RAx Fa3 Fr3 x RAy Fa2 Fr2 RBy l1 l2 l3Вертикальная плоскость
- 5,7
-42,2
Горизонтальная плоскость -15,6
- 92
Результирующая эпюра
-15,6
62,492
Рисунок 6.2 – Эпюры изгибающих моментов
Проверочный расчет вала на прочность проводим при совместном действии изгиба и кручения путем определения коэффициентов запаса прочности в опасных сечениях и сравнении их с допускаемыми.Как видно из эпюр, опасное сечение возникает в опоре В. Момент в этом сечении равен
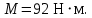
Коэффициент запаса прочности определяется по формуле:
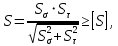
где
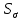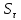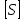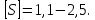
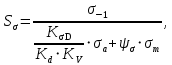
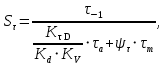
- коэффициент запаса по изгибным напряжениям; - коэффициент запаса по крутящим напряжениям; - допускаемое значение коэффициент запаса, где
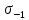- предел выносливости для материала вала при симметричном изгибе 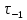- предел выносливости для материала вала при симметричном изгибе; 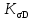, 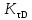- эффективные коэффициенты концентрации напряжений; 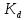- коэффициент влияния абсолютных размеров поперечного сечения; 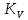- коэффициент влияния поверхностного упрочнения;
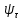- коэффициент чувствительности к асимметрии цикла напряжений; 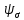- коэффициент чувствительности к асимметрии цикла напряжений; 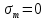- среднее напряжение цикла; 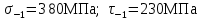; ;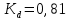 ; ;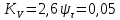 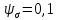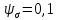. 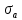- амплитудное напряжение цикла, определяемое по формуле: 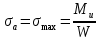,где
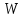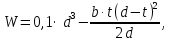
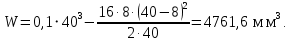
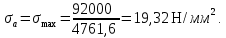
- осевой момент сопротивления сечения вала, определяемый: 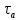- амплитудное напряжение; 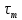- среднее напряжение цикла, определяемое по формуле: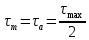 где
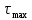- максимальное напряжение, определяемое по формуле: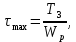 где
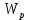- полярный момент сопротивления сечения вала, определяемый по: