Файл: Минобрнауки россии федеральное государственное бюджетное образовательное учреждение высшего образования Балтийский государственный технический университет военмех.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 181
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Решение обратной задачи кинематики с помощью матрицы Якоби
Построение траектории движения схвата манипулятора на заданном участке
Расчёт механической части мехатронного модуля робота
Расчёт второго планетарного редуктора
Проверка рассчитанного механического преобразователя
Угловая скорость, положение и скорость схвата:
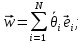 (11)
(11)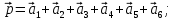 (12)
(12)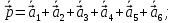 (13)
(13)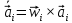 (14)
(14)Для синтеза матрицы Якоби необходимо определить матрицы А и В размерностью 3х6:
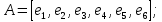 (15)
(15)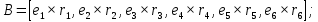 (16)
(16)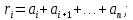 (17)
(17)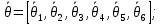 (18)
(18)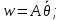 (19)
(19)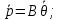 (20)
(20)Теперь определим матрицу Якоби:
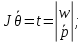 (21)
(21)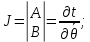 (22)
(22)При этом ускорения обобщённых координат:
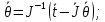 (23)
(23)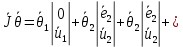
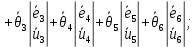 (24)
(24)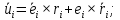 (25)
(25)-
Реализация в Matlab
Ниже представлено численное нахождение матрицы Якоби, а также визуализации ИУ РТК с помощью Matlab Robotics Systems Toolbox. Код реализации представлен в Приложении Б.
Зададим случайное положение звеньев манипулятора:
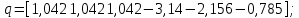
Матрица Якоби в таком случае будет иметь следующий вид:
Jacob =
-0.0000 -0.8660 -0.8660 0.2500 -0.8660 0.4330
0.0000 0.5000 0.5000 0.4330 0.5000 0.7500
1.0000 0.0000 0.0000 0.8660 0.0000 -0.5000
-5.9250 -0.4750 -1.2250 -1.6454 -0.3000 0
3.4208 -0.8227 -2.1218 0.9500 -0.5196 0
0.0000 -6.8416 -4.2435 -0.0000 -1.0392 0
Результаты визуализации представлены на рисунке 5:
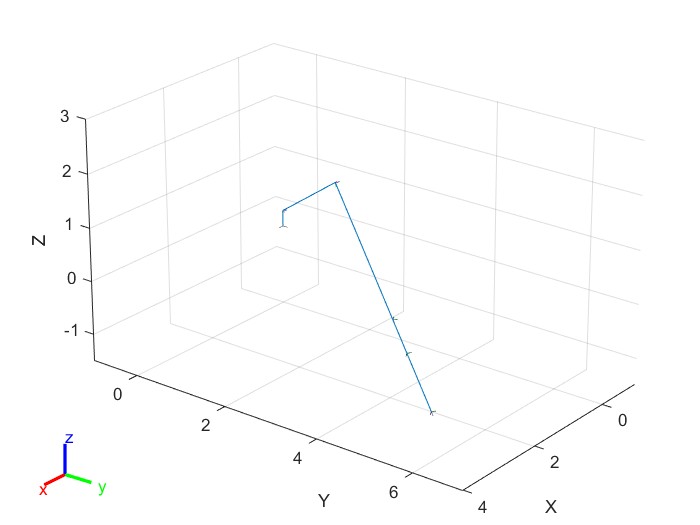
Рисунок 6 – Заданное положение ИУ РТК
Матрица Якоби будет использована в дальнейшем для построения траектории, определения энергетических параметров манипулятора, а также для вычисления ошибки.
- 1 2 3 4 5 6 7 8 9 10
Построение траектории движения схвата манипулятора на заданном участке
Опираясь на полученные ранее данные, построим траекторию движения схвата манипулятора на заданном участке, воспользовавшись пакетом Matlab Robotics Systems Toolbox и задав следующие ограничения для скорости и ускорения:
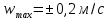
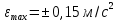
Зададим начальное и конечное положения манипулятора:
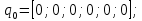

В процессе расчёта Matlab Robotics Systems Toolbox решает обратную задачу кинематики и визуализирует положение манипулятора.
Начальное положение манипулятора представлено на рисунке 7:
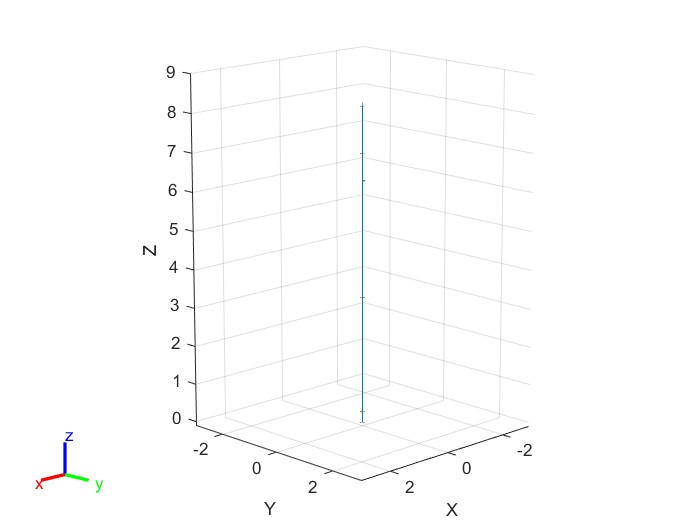
Рисунок 7 – Начальное положение манипулятора
Теперь, опираясь на решение обратной задачи кинематики, выведем графики обобщённых координат, скоростей и ускорений в обобщённых координатах для каждого звена. Графики представлены на рисунках 7–9.
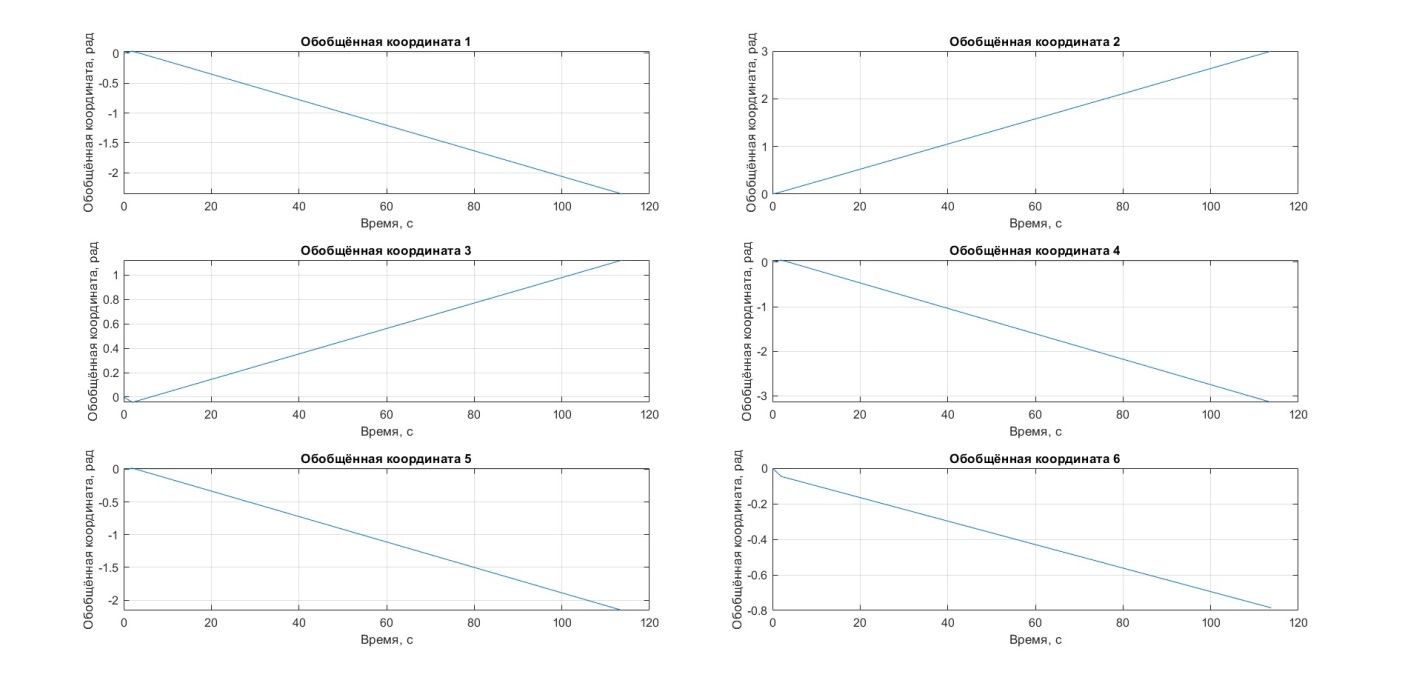
Рисунок 7 – Обобщённые координаты
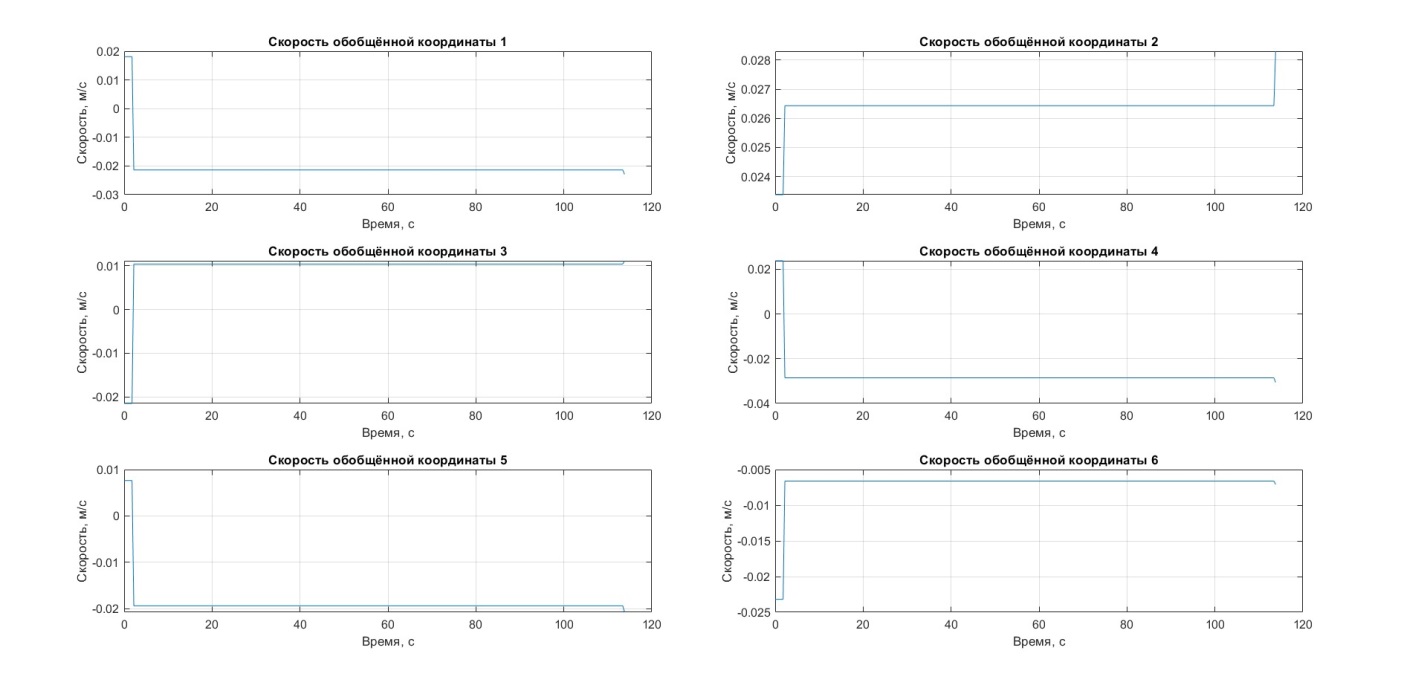
Рисунок 8 – Скорость по обобщённым координатам
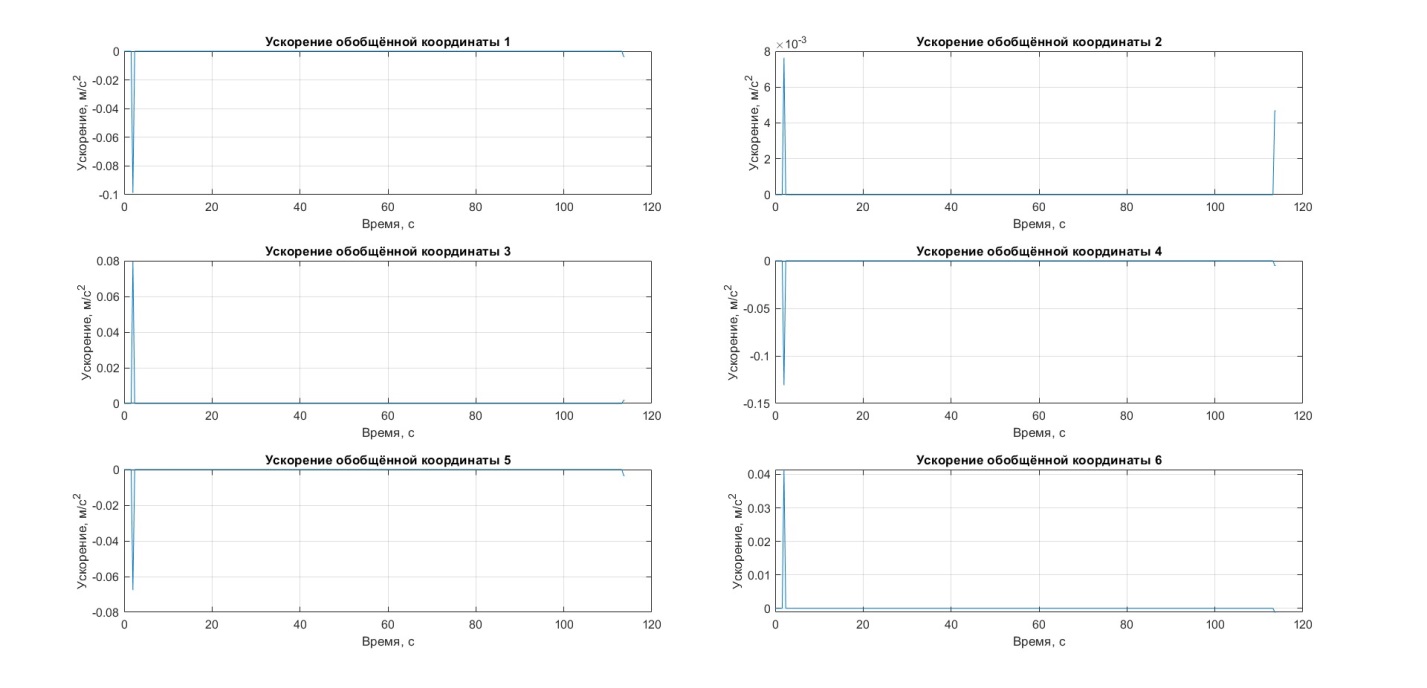
Рисунок 9 – Ускорение по обобщённым координатам
Значения обобщённых координат, их скоростей и ускорений также отвечают заданным требованиям и находятся в пределах допустимых значений, что подтверждает правильность решенных задач и возможность успешного управления.
Приведем конечное положение манипулятора на рисунке 10:
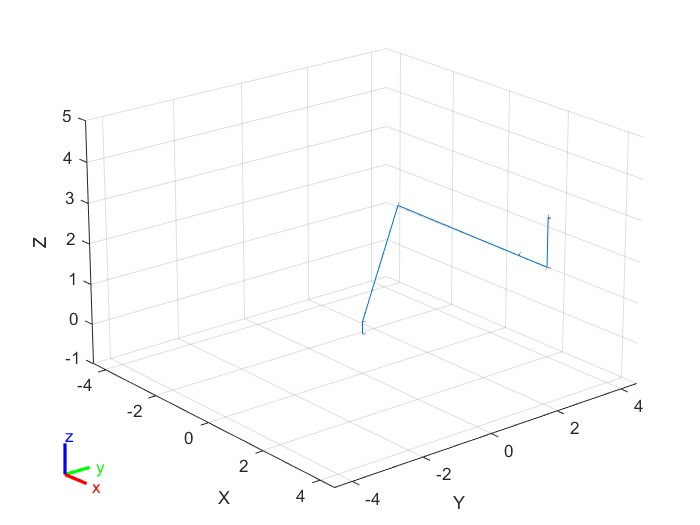
Рисунок 10 – Конечное положение манипулятора
Программный код представлен в приложении В.
-
Оценка допустимых кинематических погрешностей приводов
На основе полученных данных вычислим вектор ошибок для схвата манипулятора. Для этого зададимся следующей статической ошибкой:
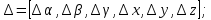
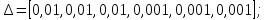
Ошибка манипулятора:
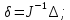 (26)
(26)Так как для этого достаточно провести итерации для первых трёх обобщённых координат, зададим для них следующие крайние положения:
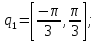
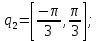
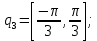
Для количества итераций, равных N=10 получим следующий результат:
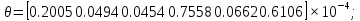
Полученные погрешности будут использованы в дальнейшем при проектировании приводов мехатронных модулей ИУ РТК.
Программный код представлен в приложении Г.
В заключение представим общий вид манипулятора без груза и схвата:
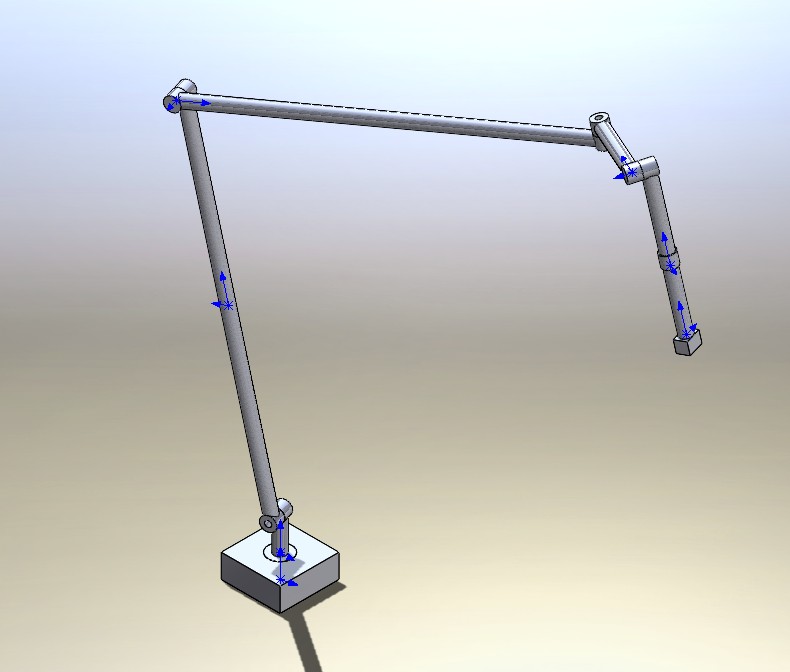
Рисунок 11 – общий вид ИУ РТК
Чертёж общего вида представлен в приложении Е.
-
Разработка электромеханического привода мехатронного модуля
-
Синтез функциональной и кинематической схем мехатронного модуля робота
-
Выполним расчёт пятого мехатронного модуля: выполним подбор двигателя и системы управления, проектировочный расчёт механического преобразователя. Для этого примем допущение, что шестой мехатронный модуль уже рассчитан, его параметры известны.
Функциональная схема мехатронного модуля представлена на рисунке 8:
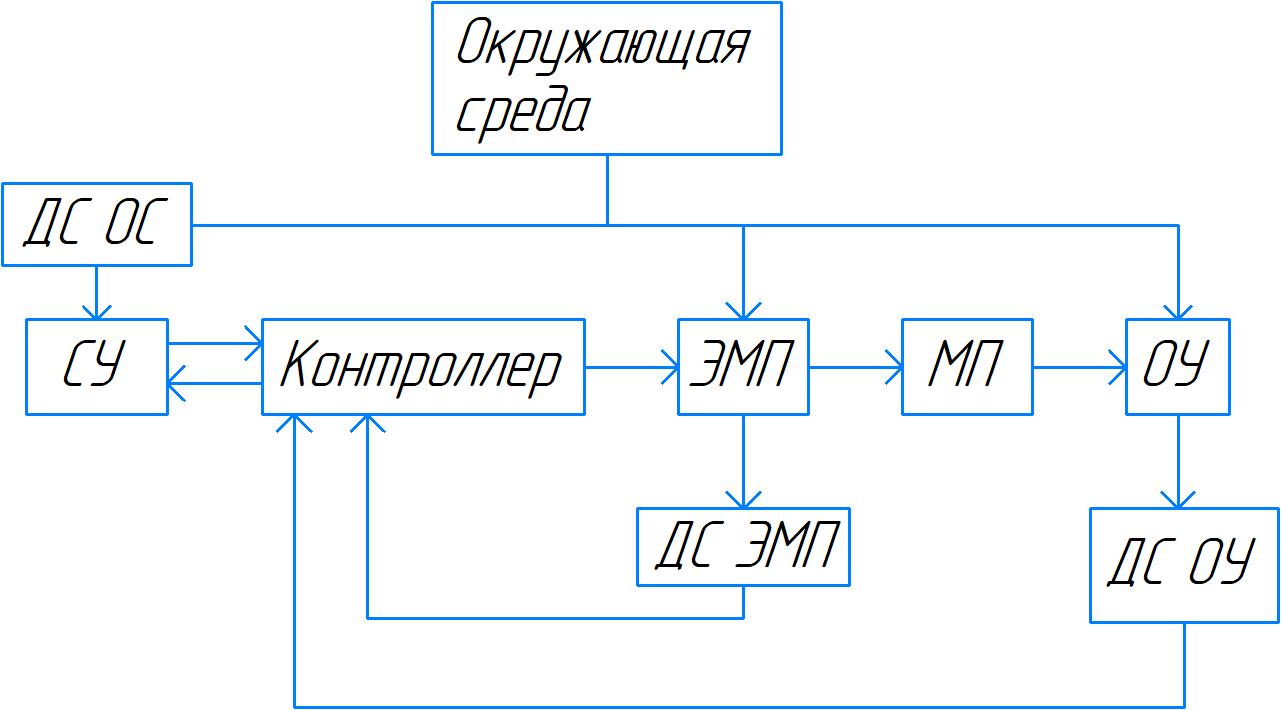
Рисунок 12–функциональная схема ММ ИУ РТК
Где:
СУ – система управления;
ДС ОС – датчики состояния окружающей среды;
ЭМП – электромеханический преобразователь, т.е. электродвигатель;
МП – механический преобразователь, т.е. редуктор;
ОУ – объект управления, т.е. шестой мехатронный модуль;
ДС ЭМП – датчики состояния электромеханического преобразователя;
ДС ОУ – датчики состояния объекта управления.
Кинематическая схема силовой части мехатронного модуля представлена на рисунке 9:
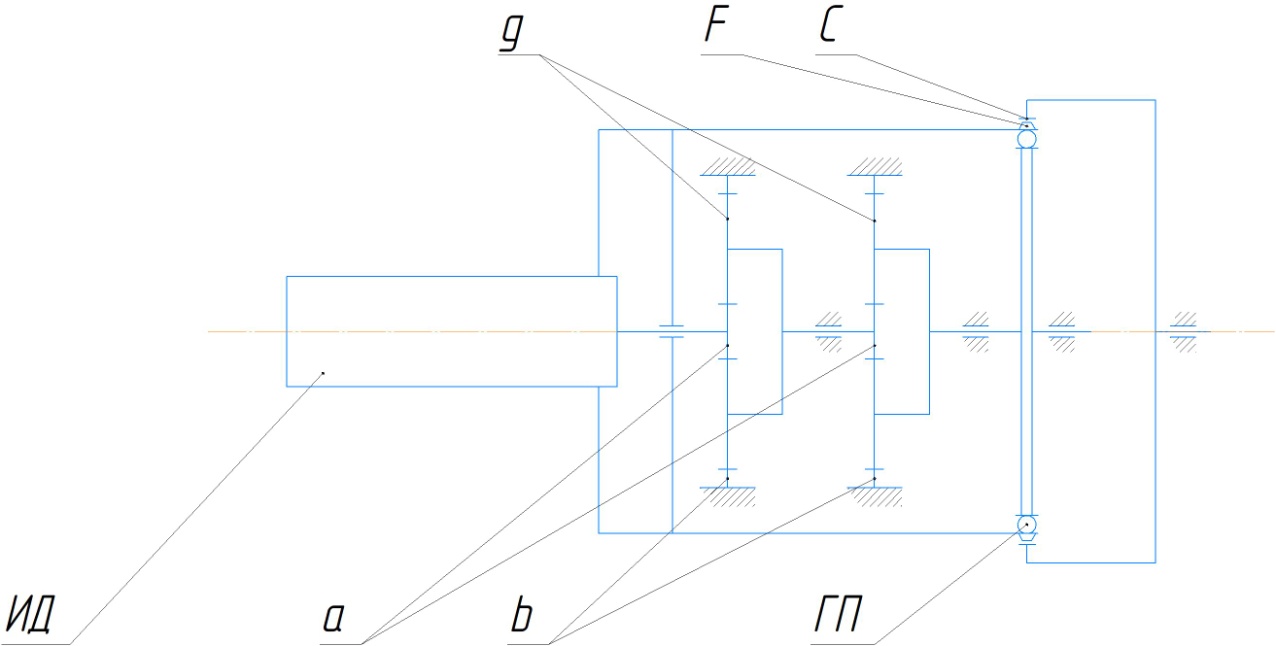
Рисунок 13 - Кинематическая схема
Где:
ИД – исполнительный двигатель;
a – солнечное колесо планетарного редуктора;
b – коронное колесо;
g – сателлит;
ГП – гибкий подшипник;
С – жесткое колесо;
F – гибкий стакан.
Предполагается, что планетарный редуктор соединен с валом двигателя, а волновой – с выходным валом планетарного редуктора. Это обусловлено тем, что волновой редуктор, в отличие от планетарного, имеет ограничения на максимальную скорость вращения элементов. В связи с этим планетарный редуктор часто используется как перемычка между валом двигателя и волновым редуктором, снижая скорость вращения до приемлемых значений. Входным звеном здесь является вал исполнительного двигателя, выходным – жесткое колесо волнового редуктора [12].
- 1 2 3 4 5 6 7 8 9 10
Выбор электропривода
Сведем требуемые параметры, которые он должен обеспечивать, а также известные данные в таблицу.
Таблица 5 – Параметры, необходимые для расчёта мехатронного модуля
| Параметр | Значение |
| Приведенный момент | 8500Нм |
| Максимальная скорость | 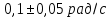 |
| Внешний радиус балки следующего мехатронного модуля | 0,0275 м |
| Внутренний радиус балки следующего мехатронного модуля | 0,022 м |
| Масса следующего мехатронного модуля | 10 кг |
| Длина следующего мехатронного модуля | 0,5 м |
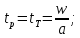 (27)
(27)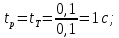
tp – время разгона
tт – время торможения
Расчет ускорения двигателя:
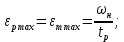 (29)
(29)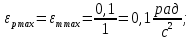
Расчёт приведенного момента инерции:
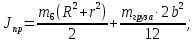 (31)
(31) Где:
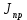 – приведенный к двигателю момент инерции;
– приведенный к двигателю момент инерции;R – внешний радиус балки;
r – внутренний радиус балки;
b – грань куба условного груза.
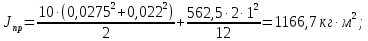
Расчет мощности двигателя (минимальная требуемая мощность)
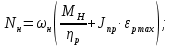 (32)
(32)Где:
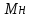 – максимальный момент нагрузки на выходном звене;
– максимальный момент нагрузки на выходном звене;