Файл: Минобрнауки россии федеральное государственное бюджетное образовательное учреждение высшего образования Балтийский государственный технический университет военмех.docx

Функциональная схема РТК

Прежде всего, в процессе создания робота-манипулятора необходимо разработать функциональную схему робототехнического устройства [7]. Данная схема представлена на рисунке 4.



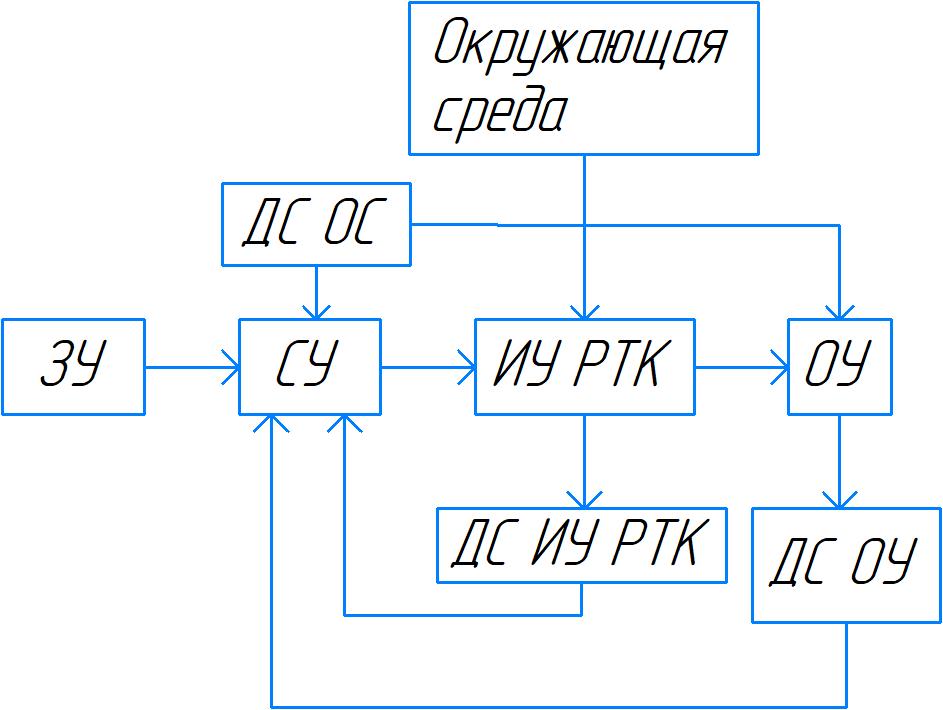
Рисунок 4 —Функциональная схема робототехнического устройства

Где:

ЗУ – задающее устройство;

СУ – система управления;

ИУ РТК – исполнительное устройство робототехнического комплекса (манипулятор);

ОУ – объект управления;

ДСИУ РТК – датчики состояния исполнительного устройства;

ДС ОС – датчики состояния окружающей среды;

ДСОУ – датчики состояния объекта управления.

2. Кинематическая схема ИУ РТК

Структурный анализ выполняется по формуле Малышева:

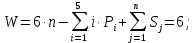(1)

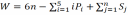
Где:

т– число подвижных звеньев;

i–Класс кинематической пары;

P_i – Число кинематических пар i-го класса

j– номер замкнутого контура;

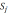
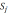– число избыточных связей замкнутого контура

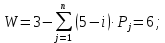(2)


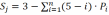
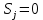
Основные параметры манипулятора приведены в таблицах 1-3.

Таблица 1 — Параметры исполнительного устройства

Параметры ИУ	Значения
Степень подвижности	W=6
Число замкнутых контуров	0

Примечание: на данном этапе в качестве звеньев принимаем эквивалентные им металлические балки с сечением в виде кольца - трубки.

---

Таблица 2 – длины звеньев манипулятора, мм

L1	L2	L3	L 4	L 5	L 6
300	3000	3000	700	700	500

Разработку исполнительного органа следует начинать с синтеза кинематической схемы.

Исполнительное устройство сервисного робота-манипулятора космического назначения имеет кинематическую схему, состоящую из 6 звеньев с вращательными кинематическими парами 5-ого класса. Данная схема представлена на рисунке 5.



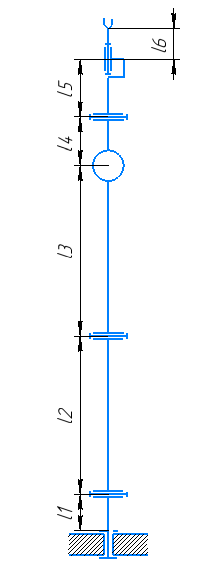
Рисунок 5 — Кинематическая схема исполнительного устройства

4. Решение прямой задачи кинематики

Обратная задача кинематики заключается в расчете обобщенных координат при заданных линейных и угловых координатах рабочего органа манипулятора.

Прямая задача кинематики решается определением параметров Денавита-Хартенберга и последующим вычислением матрицы инструмента для определения положения схвата [8].

Для решения прямой задачи кинематики сформируем параметры Денавита-Хартенберга, внеся их в таблицу 4:

Таблица 3 – параметры Денавита-Хартенберга манипулятора

	θ	α	d	a
1			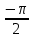0	l1
2		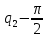0	l2	0
3		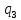	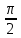l3	0
4		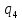	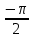l4	0
5		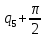	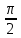0	0
6		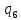0	0	l5+l6

---

Где 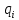– обобщенные координаты:

– угол поворота звена 1 относительно оси ;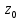

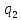– угол поворота звена 2 относительно оси ;

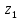– угол поворота звена 3 относительно оси ;

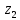– угол поворота звена 4 относительно оси ;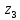

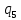– угол поворота звена 5 относительно оси ;

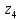– угол поворота инструмента относительно оси .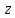



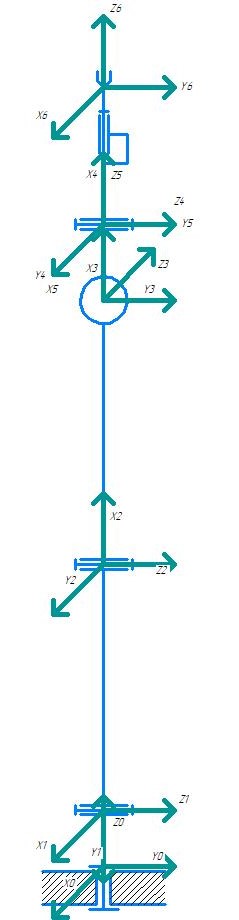
Рисунок 6 — Параметры Денавита-Хартенберга исполнительного устройства

Для дальнейшего проектирования необходимо решить прямую и обратную задачи кинематики.

Для расчета матрицы инструмента определим последовательность согласованных систем координат.

Составим расширенные однородные матрицы преобразований в системе координат присоединенных звеньев робота .

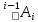Матрица преобразования для 1-го звена имеет вид:



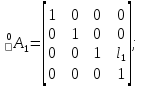
Для 2-ого звена:



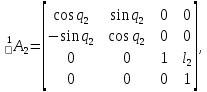
Для 3-го звена:



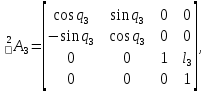
Для 4-го звена:



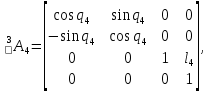
Для 5-го звена:



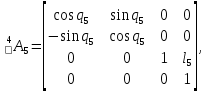
Для 6-го звена:



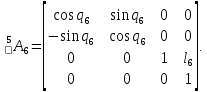
Матрица инструмента представляет собой произведение последовательности однородных матриц преобразования

---

и имеет вид: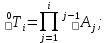







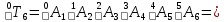
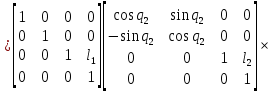
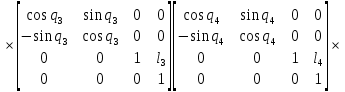
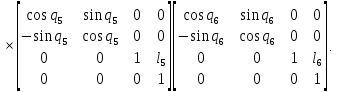(3)

Проверим правильность синтеза матрицы инструмента, используя программный код в Matlab [9]. Результат работы программы:
T1 =

1 0 0 0

0 1 0 0

0 0 1 300

0 0 0 1

T2 =

1 0 0 0

0 1 0 0

0 0 1 3000

0 0 0 1

T3 =

1 0 0 0

0 1 0 0

0 0 1 3000

0 0 0 1

T4 =

1 0 0 0

0 1 0 0

0 0 1 700

0 0 0 1

T5 =

1 0 0 0

0 1 0 0

0 0 1 700

0 0 0 1

T6 =

0 -1 0 0

0 0 0 0

0 0 1 500

0 0 0 1



Рисунок 5 – Заданное положение ИУ РТК

Программный код представлен в приложении А.

Положение схвата в начальной системе координат 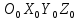определяется следующим выражением:

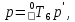(4)

где 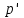– координаты схвата в СК .

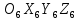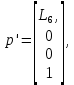(5)

где 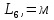– длина 6 звена.

Реализация в Matlab представлена в Приложении Б.

Зададим начальное положение манипулятора:

При :

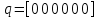T =

[-1, 0, 0, -3000]

[ 0, -1, 0, 3700]

[ 0, 0, 1, 1500]

[ 0, 0, 0, 1]

p =

-3000

3700

1500

1
Зададим случайное положение манипулятора:

При :
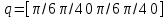T =

[0.0002 0.0007 0.0006 -3.1103]³

[-0.0003 -0.0006 0.0008 2.5725]³

[0.0009 -0.0004 0.0001 3.1973]³

[0, 0, 0, 1]

p =

-3.1103³

2.5725³

3.1973³

1
Таким образом, решена прямая задача кинематики для ИУ робота.

4. 1   2   3   4   5   6   7   8   9   10

---

Решение обратной задачи кинематики с помощью матрицы Якоби

1. Определение матрицы Якоби

Следующим этапом является решение обратной задачи кинематики.

Положение схвата манипулятора относительно начальной системы координат однозначно определяется его обобщенными координатами, а именно [10]:

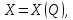(6)

Где:

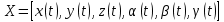– вектор абсолютных координат;

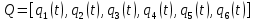- вектор обобщенных координат манипулятора.

Продифференцировав 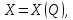получим:

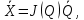(7)

Где:

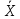– агрегированный вектор линейных и угловых скоростей рабочего органа;

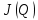– матрица Якоби, которая имеет следующий вид:

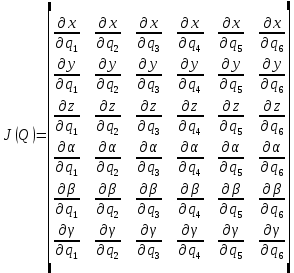(8)

Таким образом, выражение (7) принимает следующий вид:

(9)

Произведем синтез матрицы Якоби [11]:

Векторы угловых скоростей:













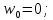
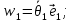
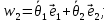
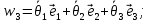
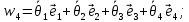
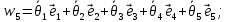
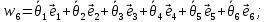(10)
Где:

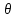–угол вращения;

е–ось вращения.

---