Файл: 1. Свет. Интерференция света. Условие максимума и минимума интерференции.docx

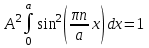, (1.17)

взяв этот интеграл, получаем 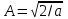и в результате имеем конечное выражение для возможных решений уравнения Шредингера в поставленной задаче

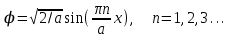. (1.18)

Данное решение показывает, что поведение микрочастицы в одномерной бесконечно глубокой потенциальной «яме» может быть различным в зависимости от значения числа n, его называют квантовым числом и рассматривают как номер возможного состояния микрочастицы.

Рассмотрим графики функции ² (рис.5), которая согласно (1.8) определяет вероятность нахождения частицы в разных точках «ямы» для различных состояний.



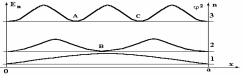
Рис.5. Графики вероятности нахождения частицы в бесконечно глубокой потенциальной «яме» для n = 1, 2, 3. Горизонтальные, тонкие линии соответствуют значениям энергий состояний (энергетическая диаграмма или уровни возможных энергий системы), толстые линии соответствуют функции ².

Из рисунка 5 видно, что во втором и в третьем состояниях микрочастица не может находиться в некоторых точках «ямы» A,B,C, однако она может находиться между этими точками. Кроме этого, видно, что минимальное значение полной энергии Е₁, которая в области 2 является кинетической энергией, не равна нулю, это означает что частица находится в непрерывном движении. Такое поведение микрочастицы существенно отличается от поведения макрочастиц и приводит к тому, что в квантовой механике не может быть использовано классическое понятие траектории.

Используя найденные соотношения ka = n и (1.16), получим выражение для полной энергии частицы

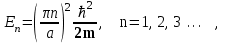(1.19)

которое показывает, что энергия частицы в разных состояниях различна и строго определена (имеет дискретный спектр). Других значений энергии частица иметь не может, возможные дискретные значения называют квантовыми уровнями энергии. Подобное квантование у микрочастиц может происходить и с другими параметрами: импульсом, моментом импульса.

Если рассмотреть таким же образом более реальную ситуацию, когда частица находится в одномерной потенциальной «яме» конечной глубины (U = Uo в областях 1,3 для x < 0 и x > a; U = 0 в области 2 для 0 > x > a), то, в отличие от случая бесконечно глубокой ямы, функция 

---

² не будет равна нулю в областях 1, 3 даже при малых энергиях частицы (рис.6).



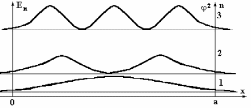
Рис.6. Графики вероятности нахождения частицы в потенциальной «яме» конечной глубины для n = 1, 2, 3.

Это означает, что частица может выйти за пределы потенциальной «ямы» даже в случае, когда ее энергия меньше Uo , чего в классической механике происходить не может. Подобное явление наблюдается и при рассмотрении поведения микрочастицы вблизи одномерного потенциального «барьера» (U = 0 в областях 1,3 для x < 0 и x > a; U = Uo в области 2 для 0 > x > a). Если решить уравнение Шредингера в этом случае, то можно обнаружить, что частица с энергией меньшей Uo может проходить сквозь этот «барьер».

Такие явления прохождения сквозь потенциальные барьеры частиц с малой энергией являются чисто квантовыми и называются «туннельными эффектами». Экспериментально эти явления наблюдаются с микрочастицами в различных ситуациях: автоэлектронная эмиссия – выход электронов за пределы металлов при малых температурах, автоионизация – выход электронов из атомов и молекул под действием слабого электрического поля, когда энергии поля бывает недостаточно для вырывания электрона с точки зрения классической механики. В физике элементарных частиц подобное явление наблюдается в радиоактивном излучении при выходе альфа частиц из ядер атомов.

Очень важным для атомной физики является рассмотрение поведения микрочастицы в силовом поле, когда потенциальная энергия зависит от координаты x в соответствии с законом 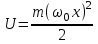, этот случай соответствует в классической механике гармоническим колебаниям тела массой m с циклической частотой _o (гармонический осциллятор). Примерно такие колебания в мире микрочастиц происходят при движении атомов в молекуле, а также при колебаниях молекул около узлов кристаллической решетке в твердых телах.

В классической механике гармонический осциллятор может иметь любую произвольную полную энергию Е, а его максимальное смещение от положения равновесия (амплитуда колебаний) x_o ограничено и связано с энергией соотношением 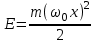. В квантовой механике для анализа характеристик особенностей движения гармонического осциллятора необходимо решить уравнение Шредингера с данной потенциальной энергией

---

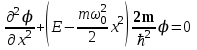. (1.20)

Решение такого дифференциального уравнения в аналитическом виде достаточно сложно, но качественные особенности аналогичны предыдущим случаям. На рисунке 7 представлены графики получаемого решения и возможные значения энергий.



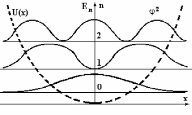
Рис.7. Графики вероятности нахождения гармонического осциллятора для n = 0, 1, 2. Горизонтальные, тонкие линии показывают значения энергий состояний (энергетическая диаграмма или уровни возможных энергий системы), толстые линии показывают ², пунктирная – вид потенциала.

Возможные значения для полной энергии при решении определяются формулой

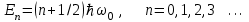. (1.21)

Из этой формулы видно, что полная энергия гармонического осциллятора тоже квантована, а ее минимальная величина при n = 0 отлична от нуля, также как и в предыдущих случаях. Наличие энергии нулевых колебаний – это чисто квантовый эффект, он говорит о том, даже в области нулевой потенциальной энергии у частицы имеется ненулевая кинетическая энергия и ненулевой импульс. Это означает, что микрочастица постоянно двигается и не может находиться в абсолютном покое.

Подтверждение наличия нулевых колебаний было получено в экспериментах по рассеиванию света в кристаллах. Согласно классической теории, при абсолютном нуле температуры по Кельвину колебаний атомов около узлов кристаллической решетки и соответственно рассеивания света, вызываемого этими колебаниями, не должно быть. Эксперименты показывают, что интенсивность рассеянного света при уменьшении температуры уменьшается, но даже при температурах очень близких к абсолютному нулю интенсивность рассеянного света не нулевая, что доказывает наличие нулевых колебаний.

Все выше приведенные варианты решений уравнения Шредингера и наличие в экспериментах эффектов, объясняемых рассмотренными примерами, указывают на необходимость использования квантово-механического описания поведения микрочастиц.

23. Модель атома по Резерфорду. Постулаты Бора.

Английский ученый Резерфорд, пропуская альфа-частицы с большой кинетической энергией через тонкие металлические пластинки, установил, что большая часть частиц отклоняются от первоначального направления на небольшие углы. Наряду с рассеиванием на малые углы, было обнаружено отклонение отдельных частиц и на большие углы, доходящие до 180

---

⁰ (Рис.1). Такое рассеивание было обнаружено и при прохождении альфа-частиц через газы.

Р
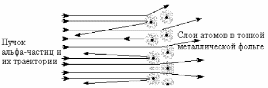
ис.1. Схема опытов Резерфорда.

При анализе этих экспериментов было установлено, что отклонения происходят вследствие кулоновского отталкивания от положительного заряда, сосредоточенного в очень малом объеме внутри атома. До этого уже было известно (по экспериментам с ионизацией газов), что в составе атомов вещества также имеются элементарные частицы – электроны (с малой массой и отрицательным зарядом). Для объяснения результатов рассеивания Резерфорд в 1911г. предложил планетарную модель атома. Согласно этой модели атом построен по типу Солнечной системы - в центре атома в очень малой области (10^-14 м) находится положительно заряженное ядро, в котором сосредоточена почти вся масса атома, а вокруг ядра под действием сил Кулоновского притяжения двигаются по замкнутым орбитам электроны (примерный радиус орбит -10^-10м). При этом суммарный заряд электронов равен по величине заряду ядра, поэтому в целом атом нейтрален. При прохождении альфа-частиц через такой атом, только малая часть частиц будет сталкиваться с ядром и рассеиваться назад, основная их часть будет проходить на больших расстояниях от ядра и, вследствие малости Кулоновских сил, будут отклоняться на небольшие углы.

Таким образом, планетарная модель атома полностью объяснила эксперименты по рассеиванию. Однако, согласно классической электродинамике электрон, двигающийся по орбите вокруг ядра должен испускать электромагнитные волны непрерывного спектра частот. При этом он теряет свою энергию и через малый интервал времени (10^-8 с) должен упасть на ядро, то есть такой атом нестабилен и имеет очень малое время жизни. Но, как известно, атомы отличаются большим временем жизни. Кроме того, из экспериментов по изучению частотного состава излучения (спектров) отдельных атомов в газах, известно, что атомы в невозбужденном (нормальном) состоянии не испускают электромагнитные волны, они излучают их только после передачи им энергии (при возбуждении), при зтом спектр частот имеет дискретный характер. Например, у атома водорода было обнаружено несколько серий частот излучения, наиболее известные описываются соотношениями:

---

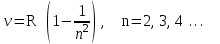
(1.1)

серия Лаймана для ультрафиолетового излучения,

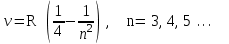(1.2)

серия Бальмераа для видимого излучения

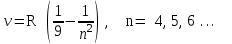(1.3)

серия Пашена для инфракрасного излучения, здесь R-постоянная Ридберга, n – номер частоты (номер линии спектра излучения) в серии. Эксперименты по изучению спектра поглощения электромагнитного излучения для атома водорода показали, что спектр поглощения тоже имеет дискретный характер, описываемый соотношениями (1.1‑1.3). Подобная дискретность спектров была обнаружена у всех атомов. Таким образом, планетарная модель атома требовала серьезных доработок.

Для объяснения спектров излучения и поглощения атома водорода в 1913г. датский ученый Бор добавил к этой модели три ограничения (постулата), которые не соответствовали законам классической механики.

1. Атом может находиться в различных состояниях, в этих состояниях электрон двигается по определенным стационарным орбитам без излучения и без потери энергии. Эти орбиты называют Боровскими орбитами.

2. При движении по Боровским орбитам электрон имеет строго определенный (дискретный) момент импульса L(L равен произведению массы электрона, его скорости и радиуса орбиты). Его значение задается формулой квантования Бора.



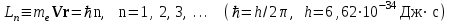
где момент импульса связывается с постоянной Планка h и квантовым числом n.

Квантовое число n является номером состояния атома и номером Боровской орбиты электрона. В этих состояниях радиусы орбит электрона и его скорости различны, атом также имеет различные энергии. Обычно атом находится в основном или невозбужденном состоянии n=1 с наименьшим значением энергии, состояния с n = 2, 3, 4 имеют большие энергии и называются возбужденными.

3. При передаче атому энергии он переходит в какое-либо возбужденное состояние с n = 2, 3, 4… (если передача энергии производится с помощью электромагнитного излучения, то происходит поглощение атомом порции излучения), в возбужденном состоянии атом находится недолго (10^-8с), он испускает порцию (квант) электромагнитного излучения и переходит в какое-либо состояние с меньшим квантовым числом. При всех переходах, в соответствии с законом сохранения, энергия кванта  точно равна разности энергий атома  = E

---