Файл: 1. Свет. Интерференция света. Условие максимума и минимума интерференции.docx

Существует также внутренний фотоэффект – это вызываемые электромагнитным излучением переходы электронов внутри полупроводника или диэлектрика из связанных состояний в свободные без вылета наружу. В результате этого концентрация свободных носителей тока внутри тела увеличивается, что приводит к повышению электропроводности. На основе данного явления конструируются полупроводниковые фотоэлементы. Они используются при автоматическом управлении электрическими цепями (например, в турникетах метро), в цепях переменного тока, в качестве источников тока в часах, микрокалькуляторах, в солнечных батареях на искусственных спутниках Земли, межпланетных и орбитальных автоматических станциях. С явлением фотоэффекта связаны фотохимические процессы, протекающие под действием света в фотографических материалах.

Эйнштейн выдвигает предположение, что свет сам по себе имеет корпускулярную природу, что имеет смысл смотреть на свет не как на поток волн, а как на поток частиц. Эйнштейн, вводя фотоны, совсем не отбрасывал волновую теорию света. Это видно уже из самой гипотезы о фотонах - энергия фотона пропорциональна частоте света. Можно сказать так: свет - ни волны, ни корпускулы в подлинном смысле этих слов, а нечто такое, что в опыте проявляется иногда как волны (интерференция, дифракция, поляризация), а иногда как поток корпускул, фотонов (черное излучение, фотоэффект и др.). И той и другой картиной - волновой и корпускулярной - приходится пользоваться смотря по обстоятельствам. Для описания одних явлений более подходит волновая точка зрения на свет, для описания других - фотонная. К настоящему времени построена единая непротиворечивая теория (квантовая теория поля или квантовая электродинамика). Она находится за пределами нашего курса, и мы ее (по причине сложности) не будем рассматривать, а удовлетворимся изложенной наглядной точкой зрения.

18.Эффект Комптона. Давление света.

Эффект Комптона (Комптон-эффект) — явление изменения длины волны электромагнитного излучения вследствие упругого рассеивания его электронами. Обнаружен американским физиком Артуром Комптоном в 1923 году для рентгеновского излучения. В 1927 Комптон получил за это открытие Нобелевскую премию по физике.



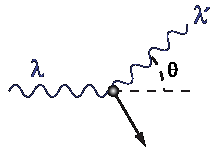
При рассеянии фотона на покоящемся электроне частоты фотона и (до и после рассеяния соответственно) связаны соотношением:

---

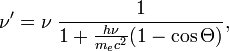
где — угол рассеяния (угол между направлениями распространения фотона до и после рассеяния).

Перейдя к длинам волн:



где — комптоновская длина волны электрона.

Для электрона м. Уменьшение энергии фотона после комптоновского рассеяния называется комптоновским сдвигом. В классической электродинамике рассеяние электромагнитной волны на заряде (томсоновское рассеяние) не сопровождается уменьшением её частоты.

Объяснить эффект Комптона в рамках классической электродинамики невозможно. С точки зрения классической физики электромагнитная волна является непрерывным объектом и в результате рассеяния на свободных электронах изменять свою длину волны не должна. Эффект Комптона является прямым доказательством квантования электромагнитной волны, другими словами подтверждает существование фотонов. Эффект Комптона является ещё одним доказательством справедливости корпускулярно-волнового дуализма микрочастиц.

Обратный эффект Комптона

Эффектом, обратным эффекту Комптона, является увеличение частоты света, претерпевающего рассеяние на релятивистских электронах, имеющих энергию выше, чем энергия фотонов. То есть в процессе такого взаимодействия происходит передача энергии от электрона фотону.

Энергия рассеянных фотонов определяется выражением[1]:



Где и — энергия рассеянного и падающего фотонов соответственно, K — кинетическая энергия электрона.

Обратный эффект Комптона ответственен за рентгеновское излучение галактических источников, рентгеновскую составляющую реликтового фонового излучения (эффект Сюняева — Зельдовича), трансформацию плазменных волн в высокочастотные электромагнитные волны.

Давление света.

Давление электромагнитного излучения, давление света — давление, которое оказывает световое (и вообще электромагнитное) излучение, падающее на поверхность тела.

В отсутствие рассеяния

---

Для вычисления давления света при нормальном падении излучения и отсутствии рассеяния можно воспользоваться следующей формулой:



где — количество лучистой энергии, падающей нормально на 1 м² поверхности за 1 с, т. е. интенсивность падающего излучения; — скорость света, — коэффициент пропускания, — коэффициент отражения.

Давление солнечного света на перпендикулярную свету зеркальную поверхность, находящуюся в космосе в районе Земли, легко рассчитать через плотность потока солнечной (электромагнитной) энергии на расстоянии одной астрономической единицы от Солнца (солнечная постоянная). Оно составляет 4,6 мкН/м² = 4,6·10−11[источник не указан 494 дня] атм (см. солнечная постоянная).

Если свет падает под углом к нормали, то давление можно выразить формулой:



где — объёмная плотность энергии излучения, — коэффициент пропускания, — коэффициент отражения, — единичный вектор в направлении падающего пучка, — единичный вектор в направлении отражённого пучка.

Например, тангенциальная составляющая силы давления света на единичную площадку будет равна:



Нормальная составляющая силы давления света на единичную площадку будет равна:



Отношение нормальной и тангенциальной составляющих равно:



При рассеянии

Если рассеяние света поверхностью и при пропускании, и при отражении подчиняется закону Ламберта, то при нормальном падении давление будет равно:

где — интенсивность падающего излучения, — коэффициент диффузного пропускания, — альбедо.

Вывод

Найдём импульс, уносимый электромагнитной волной от Ламбертова источника.

Полная светимость ламбертова источника, как известно, равна:

---

где — сила света в направлении нормали.

Отсюда сила света под произвольным углом к нормали, по закону Ламберта, равна:

.

Энергия, излучаемая в элемент телесного угла, имеющий вид сферического кольца, равна:



Для определения импульса, уносимого излучением, нужно учитывать только его нормальную составляющую, так как в силу поворотной симметрии все тангенциальные составляющие взаимно компенсируются:



Отсюда



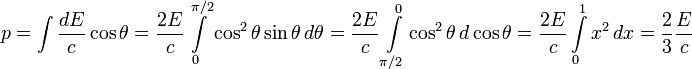
Для рассеянного обратно излучения и

Для излучения, прошедшего сквозь пластинку, и (минус возникает из-за того, что это излучение направлено вперёд).

Складывая давление, создаваемое падающим и обоими видами рассеянного излучения, получаем искомое выражение.

В случае, когда отражённое и пропущенное излучение является частично направленным и частично рассеянным, справедлива формула:



где — интенсивность падающего излучения, — коэффициент направленного пропускания, — коэффициент диффузного пропускания, — коэффициент направленного отражения, — альбедо рассеяния.

19.Гепотиза Де-Бройля. Формула Де-Бройля. Опыт подтверждающий волновый свойства микрочастиц.

Как известно, эксперименты с электромагнитными волнами показали, что в некоторых явлениях они проявляют свойства частиц (фотоэффект, эффект Комптона, тепловое излучение и др). Эти явления удалось описать, если предположить согласно теории Планка, что электромагнитное излучение является потоком частиц‑фотонов или квантов со следующими значениями энергии и импульса

---

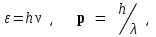(1.4)

где - частота, - длина волны.

По аналогии, Луи де Бройль в 1923 году выдвинул гипотезу, что для объяснения волновых свойств микрочастиц им необходимо сопоставить особые волны, которые были названы волнами де Бройля. То есть, если микрочастице приписать некоторый волновой процесс длиной волны

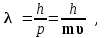(1.5)

(где р, m, υ – импульс, масса и скорость частицы), то по формулам дифракции и интерференции для электромагнитных волн можно рассчитать эти явления и для пучков микрочастиц. Например, по известной формуле оптики для дифракционной решетки dSin(_k) = k можно рассчитать положения максимумов и при дифракции микрочастиц. Эта гипотеза нашла полное подтверждение в вышеупомянутых экспериментах.

Эксперименты также показали, что распространение волн де Бройля не связано с распространением электромагнитных волн, а также каких-либо других волн, известных в классической физике. Наблюдаемое постепенное формирование интерференционной картины показывает, что волны де Бройля связаны со статистической природой движения микрочастиц и имеют вероятностное истолкование.

20. Соотношение неопределенностей Гейзенберга.

Своеобразие движения микрочастиц, как оказалось, заключается также и в том, что ее траекторию нельзя характеризовать точными значениями координат и скорости (т.е. нельзя определить одновременно положение микрочастицы в пространстве и ее скорость с произвольной точностью). Немецкий ученый Гейзенберг в 1927г. установил, что неопределенности или погрешности измерения координаты Δх, Δy, Δz и импульса Δр_х, Δр_y, Δр_z удовлетворяют соотношениям:

Δх Δр_х ≥ h, Δy Δр_y ≥ h, Δz Δр_z ≥ h. (1.6)

Подобное соотношение имеется и для неопределенности измерения времени состояния микросистемы Δt и ее энергии ΔЕ

Δt ΔЕ≥h , (1.7)

все эти формулы называются соотношениями неопределенностей Гейзенберга.

Наличие этих соотношений объяснятся тем, что при измерении одного параметра микрочастицы, второй соответствующий параметр искажается измерительным прибором и чем точнее измеряется один, тем больше искажается второй. Это происходит и для макрообъектов, но вследствие их больших масс воздействие приборов оказывается несущественным. Например, при определении координат макрообъекта путем локации используют поток фотонов, которые испускаются локатором, они со скоростью света долетают до объекта, отражаются от него и возвращаются назад. Зная время движения фотона и его скорость можно легко определить расстояние до объекта, причем вследствие массивности макрообъекта, его скорость изменится незначительно. Если же использовать принцип локации для определения координаты микрочастицы, то при отражении от нее фотона он передаст ей импульс, сравнимый с импульсом частицы, что приведет к значительному изменению ее скорости. Подобные изменения соответствующих параметров

---