Файл: 1. Свет. Интерференция света. Условие максимума и минимума интерференции.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 239
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
3. Интерференция света в тонких пленках или полосы ровного наклона.
6.Дифракция Френеля на круглом отверстии и диске.
7.Дифракция Фраунгофера на прямоугольной щели.
8. Дисперсия и разрешающая сила спектрального прибора.
Оптическая активность веществ. @
Поляризация света при отражении и преломлениина границе раздела
двух диэлектрических сред. Закон Брюстера.
4. 3. Поляризация света при двойном лучепреломлении.
6. 1. Характеристики теплового излучения. @
Волновая функция, её статистический смысл. Задание состояния микрочастицы.
28. Состав ядра. Характеристики ядра. Размеры ядер.
равновесным или черным излучением. Величина энергии равновесного излучения и его спектральный состав зависят только от температуры. Если в адиабатно замкнутую полость с зеркально отражающими стенками поместить несколько тел, нагретых до различной температуры, то, как показывает опыт, такая система с течением времени приходит в состояние теплового равновесия, при котором все тела приобретают одинаковую температуру. Если через малое отверстие заглянуть внутрь полости, в которой установилось термодинамическое равновесие между излучением и нагретыми телами, то глаз не различит очертаний тел и зафиксирует лишь однородное свечение всей полости в целом.
Для установления равновесия в полости необходимо, чтобы каждое тело испускало ровно столько лучистой энергии, сколько оно и поглощает. Это одна из важнейших закономерностей теплового излучения, экспериментально установленная Прево в 1809 г.
Рассмотрим величины, характеризующие тепловое излучение:
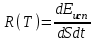
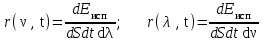
Связь энергетической светимости и испускательной способности тела записывается следующим образом:
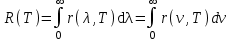
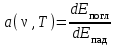
Поглощательная способность - это безразмерная величина.
И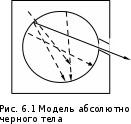 спускательная и поглощательная способности зависят от частоты излучаемых и поглощаемых волн, температуры тела, его химического состава и состояния поверхности. Все тела частично поглощают и частично отражают падающее на них излучение. Идеализацией является понятие абсолютно черного тела
спускательная и поглощательная способности зависят от частоты излучаемых и поглощаемых волн, температуры тела, его химического состава и состояния поверхности. Все тела частично поглощают и частично отражают падающее на них излучение. Идеализацией является понятие абсолютно черного тела
, поглощающего все падающее на него излучение во всем диапазоне частот. Поглощательная способность абсолютно черного тела равна единице = 1 при любой температуре T . Моделью абсолютно черного тела является небольшое отверстие в сферической полости, размер отверстия меньше 0.1 от диаметра полости (рис. 6.1). Свет, падающий через отверстие внутрь полости, после поглощения и отражения стенками будет такой системой практически полностью поглощен, и отверстие снаружи будет казаться совершенно черным. Но если полость нагрета до определенной температуры T, и внутри установилось тепловое равновесие, то собственное излучение полости, выходящее через отверстие, будет излучением абсолютно черного тела. Именно таким образом моделируется абсолютно черное тело во всех экспериментах по исследованию теплового излучения. Абсолютно черных тел в природе не бывает. В природе к абсолютно черному телу по свойствам близки: сажа, черный бархат, черная шерсть животных, поглощающие свойства которых обусловлены их пористостью. От таких тел падающее излучение не отражается из-за многократного переотражения в микрополостях и последующего рассеяния.
= 1 при любой температуре T . Моделью абсолютно черного тела является небольшое отверстие в сферической полости, размер отверстия меньше 0.1 от диаметра полости (рис. 6.1). Свет, падающий через отверстие внутрь полости, после поглощения и отражения стенками будет такой системой практически полностью поглощен, и отверстие снаружи будет казаться совершенно черным. Но если полость нагрета до определенной температуры T, и внутри установилось тепловое равновесие, то собственное излучение полости, выходящее через отверстие, будет излучением абсолютно черного тела. Именно таким образом моделируется абсолютно черное тело во всех экспериментах по исследованию теплового излучения. Абсолютно черных тел в природе не бывает. В природе к абсолютно черному телу по свойствам близки: сажа, черный бархат, черная шерсть животных, поглощающие свойства которых обусловлены их пористостью. От таких тел падающее излучение не отражается из-за многократного переотражения в микрополостях и последующего рассеяния.
Наряду с понятием черного тела используют понятие серого тела, поглощательная способность которого меньше единицы, но одинакова для всех частот и зависит только от температуры, материала, из которого сделано тело и состояния его поверхности
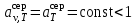 .
.
У реальных тел < 1 и зависит от частоты.
< 1 и зависит от частоты.
З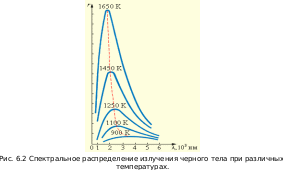 акон Стефана–Больцмана.
акон Стефана–Больцмана.
Открытие закона Кирхгофа потребовало тщательного изучения излучения абсолютно черного тела. В 1879 году польский физик Йозеф Стефан на основе анализа экспериментальных данных пришел к заключению, что энергетическая светимость абсолютно черного тела R(T) пропорциональна четвертой степени абсолютной температуры T:
R(T) = T4
Несколько позднее, в 1884 году, Л. Больцман теоретически получил эту зависимость на основе термодинамических законов. Этот закон получил название закона Стефана–Больцмана. Числовое значение постоянной Стефана-Больцмана σ составляет 5,671·10–8 Вт/(м2·К4). В дальнейшем в результате экпериментальных проверок было установлено, что такая зависимость с поправкой имеет место и для других тел.
Закон Стефана-Больцмана не позволяет найти частотную зависимость излучения.
14. Закон Кирхгофа. Закон смещения вин.
Кирхгоф (1859 г.) нашел количественную связь излучательной и поглощательной способности: отношение излучательной и поглощательной способности не зависит от природы тела и является универсальной функцией частоты и температуры, одинаковой для всех тел:
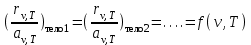 ,
,
где функция f(ν,T) называется универсальной функцией Кирхгофа. Этот закон следует из того, что для теплового равновесия количества поглощаемой и излучаемой телом энергии должны быть равны для всех диапазонов частот:
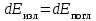 .
.
Это равенство можно переписать в следующем виде: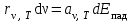 , откуда следует
, откуда следует
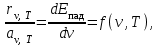
где f(ν,T)- общая для всех тел функция, характеризующая распределение энергии по частотам в падающем на тела тепловом излучении. Закон справедлив для любого тела, в том числе и для абсолютно черного. Поскольку его поглощательная способность равна единице, то из закона следует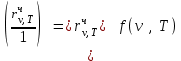 . Таким образом, универсальная функция Кирхгофа есть не что иное, как испускательная способность абсолютно черного тела. Из закона Кирхгофа следует, что испускательная способность любого тела меньше, чем абсолютно черного.
. Таким образом, универсальная функция Кирхгофа есть не что иное, как испускательная способность абсолютно черного тела. Из закона Кирхгофа следует, что испускательная способность любого тела меньше, чем абсолютно черного.
С увеличением температуры максимум смещается в область коротких длин волн, причем произведение температуры T на длину волны λm, соответствующую максимуму, остается постоянным:
λmT = b или λm = b / T.
Это соотношение было получено Вином в 1893 г. из термодинамики. Оно выражает так называемый закон смещения Вина: длина волны λm, на которую приходится максимум энергии излучения абсолютно черного тела, обратно пропорциональна абсолютной температуре T. Значение постоянной Вина b = 2,898·10–3 м·К.
При практически достижимых в лабораторных условиях температурах максимум излучательной способности r(λ, T) лежит в видимой красной и инфракрасной областях, поэтому нагретые тела приобретают красный цвет. Вид графиков (рис. 6.2) показывает, как спектральный максимум излучения смещается из инфракрасной в видимую (при
Для установления равновесия в полости необходимо, чтобы каждое тело испускало ровно столько лучистой энергии, сколько оно и поглощает. Это одна из важнейших закономерностей теплового излучения, экспериментально установленная Прево в 1809 г.
6. 1. Характеристики теплового излучения. @
Рассмотрим величины, характеризующие тепловое излучение:
-
Энергетическая светимость R(Т) - это полная энергия электромагнитного излучения, испускаемая единицей поверхности тела во всех направлениях в единицу времени на всех частотах. Этот полный поток излучения всех волн называют также интегральной светимостью тела. Согласно определению
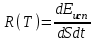
-
Распределение энергии по длинам волн в излучении тел при заданной температуре T характеризуется испускательной или излучательной способностью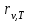 или r(ν, T), равной энергии, испускаемой с единицы поверхности тела в единицу времени в единичном интервале частот. Аналогично можно ввести распределение энергии по длинам волн r(λ, T). Функцию r(λ, T) (или r(ν, T)) часто называют спектральной плотностью энергетической светимости.
или r(ν, T), равной энергии, испускаемой с единицы поверхности тела в единицу времени в единичном интервале частот. Аналогично можно ввести распределение энергии по длинам волн r(λ, T). Функцию r(λ, T) (или r(ν, T)) часто называют спектральной плотностью энергетической светимости.
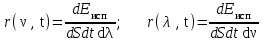
Связь энергетической светимости и испускательной способности тела записывается следующим образом:
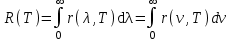
-
Способность тел поглощать падающее на них излучение характеризуется поглощательной способностью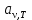 или а(ν,Т)- отношением поглощенной энергии в интервале частот от ν до ν +dν к общему количеству энергии падающего излучения в том же интервале:
или а(ν,Т)- отношением поглощенной энергии в интервале частот от ν до ν +dν к общему количеству энергии падающего излучения в том же интервале:
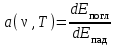
Поглощательная способность - это безразмерная величина.
И
 спускательная и поглощательная способности зависят от частоты излучаемых и поглощаемых волн, температуры тела, его химического состава и состояния поверхности. Все тела частично поглощают и частично отражают падающее на них излучение. Идеализацией является понятие абсолютно черного тела
спускательная и поглощательная способности зависят от частоты излучаемых и поглощаемых волн, температуры тела, его химического состава и состояния поверхности. Все тела частично поглощают и частично отражают падающее на них излучение. Идеализацией является понятие абсолютно черного тела
, поглощающего все падающее на него излучение во всем диапазоне частот. Поглощательная способность абсолютно черного тела равна единице
 = 1 при любой температуре T . Моделью абсолютно черного тела является небольшое отверстие в сферической полости, размер отверстия меньше 0.1 от диаметра полости (рис. 6.1). Свет, падающий через отверстие внутрь полости, после поглощения и отражения стенками будет такой системой практически полностью поглощен, и отверстие снаружи будет казаться совершенно черным. Но если полость нагрета до определенной температуры T, и внутри установилось тепловое равновесие, то собственное излучение полости, выходящее через отверстие, будет излучением абсолютно черного тела. Именно таким образом моделируется абсолютно черное тело во всех экспериментах по исследованию теплового излучения. Абсолютно черных тел в природе не бывает. В природе к абсолютно черному телу по свойствам близки: сажа, черный бархат, черная шерсть животных, поглощающие свойства которых обусловлены их пористостью. От таких тел падающее излучение не отражается из-за многократного переотражения в микрополостях и последующего рассеяния.
= 1 при любой температуре T . Моделью абсолютно черного тела является небольшое отверстие в сферической полости, размер отверстия меньше 0.1 от диаметра полости (рис. 6.1). Свет, падающий через отверстие внутрь полости, после поглощения и отражения стенками будет такой системой практически полностью поглощен, и отверстие снаружи будет казаться совершенно черным. Но если полость нагрета до определенной температуры T, и внутри установилось тепловое равновесие, то собственное излучение полости, выходящее через отверстие, будет излучением абсолютно черного тела. Именно таким образом моделируется абсолютно черное тело во всех экспериментах по исследованию теплового излучения. Абсолютно черных тел в природе не бывает. В природе к абсолютно черному телу по свойствам близки: сажа, черный бархат, черная шерсть животных, поглощающие свойства которых обусловлены их пористостью. От таких тел падающее излучение не отражается из-за многократного переотражения в микрополостях и последующего рассеяния.Наряду с понятием черного тела используют понятие серого тела, поглощательная способность которого меньше единицы, но одинакова для всех частот и зависит только от температуры, материала, из которого сделано тело и состояния его поверхности
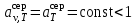 .
.У реальных тел
 < 1 и зависит от частоты.
< 1 и зависит от частоты.З
 акон Стефана–Больцмана.
акон Стефана–Больцмана.Открытие закона Кирхгофа потребовало тщательного изучения излучения абсолютно черного тела. В 1879 году польский физик Йозеф Стефан на основе анализа экспериментальных данных пришел к заключению, что энергетическая светимость абсолютно черного тела R(T) пропорциональна четвертой степени абсолютной температуры T:
R(T) = T4
Несколько позднее, в 1884 году, Л. Больцман теоретически получил эту зависимость на основе термодинамических законов. Этот закон получил название закона Стефана–Больцмана. Числовое значение постоянной Стефана-Больцмана σ составляет 5,671·10–8 Вт/(м2·К4). В дальнейшем в результате экпериментальных проверок было установлено, что такая зависимость с поправкой имеет место и для других тел.
Закон Стефана-Больцмана не позволяет найти частотную зависимость излучения.
14. Закон Кирхгофа. Закон смещения вин.
Закон Кирхгофа.
Кирхгоф (1859 г.) нашел количественную связь излучательной и поглощательной способности: отношение излучательной и поглощательной способности не зависит от природы тела и является универсальной функцией частоты и температуры, одинаковой для всех тел:
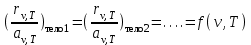 ,
,где функция f(ν,T) называется универсальной функцией Кирхгофа. Этот закон следует из того, что для теплового равновесия количества поглощаемой и излучаемой телом энергии должны быть равны для всех диапазонов частот:
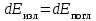 .
.Это равенство можно переписать в следующем виде:
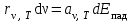 , откуда следует
, откуда следует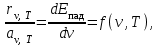
где f(ν,T)- общая для всех тел функция, характеризующая распределение энергии по частотам в падающем на тела тепловом излучении. Закон справедлив для любого тела, в том числе и для абсолютно черного. Поскольку его поглощательная способность равна единице, то из закона следует
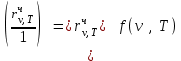 . Таким образом, универсальная функция Кирхгофа есть не что иное, как испускательная способность абсолютно черного тела. Из закона Кирхгофа следует, что испускательная способность любого тела меньше, чем абсолютно черного.
. Таким образом, универсальная функция Кирхгофа есть не что иное, как испускательная способность абсолютно черного тела. Из закона Кирхгофа следует, что испускательная способность любого тела меньше, чем абсолютно черного.С увеличением температуры максимум смещается в область коротких длин волн, причем произведение температуры T на длину волны λm, соответствующую максимуму, остается постоянным:
λmT = b или λm = b / T.
Это соотношение было получено Вином в 1893 г. из термодинамики. Оно выражает так называемый закон смещения Вина: длина волны λm, на которую приходится максимум энергии излучения абсолютно черного тела, обратно пропорциональна абсолютной температуре T. Значение постоянной Вина b = 2,898·10–3 м·К.
При практически достижимых в лабораторных условиях температурах максимум излучательной способности r(λ, T) лежит в видимой красной и инфракрасной областях, поэтому нагретые тела приобретают красный цвет. Вид графиков (рис. 6.2) показывает, как спектральный максимум излучения смещается из инфракрасной в видимую (при