Файл: Автоматики и вычислительной техники.docx

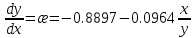
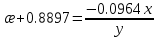
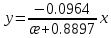
В таблице 2.1.5 представлены значения α, σ и y в зависимости от значения :

Таблица 2.1.5

0	0	-0.108	-0.108x
∞	π/2	0	0
-1	-π/4	0.874	0.874x
1	π/4	-0.051	-0.051x
-			∞

---

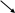
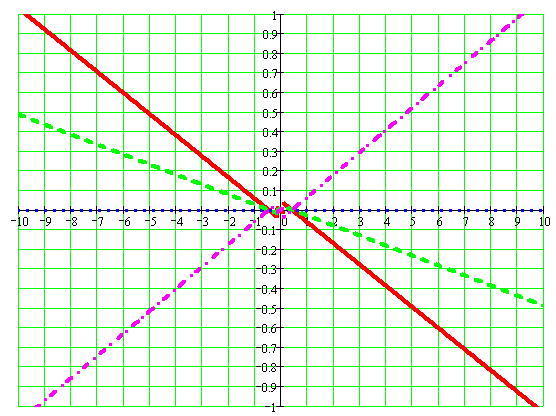
Рисунок 2.6 – График изоклин для реле с зоной нечувствительности



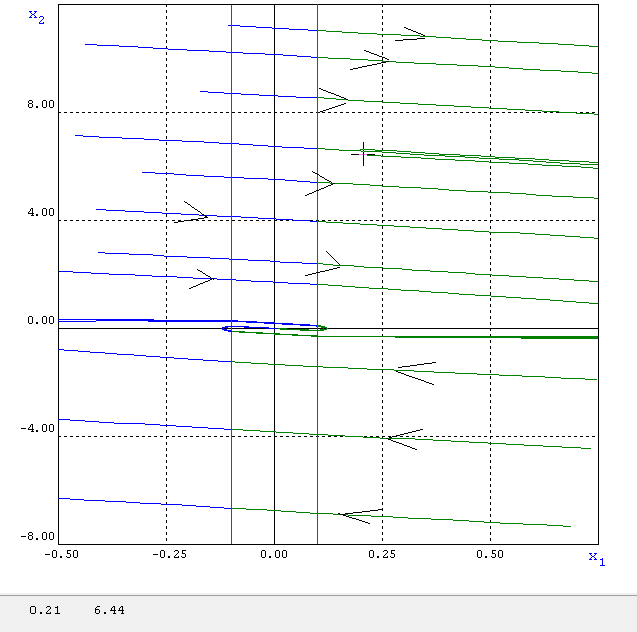
Рисунок 2.7 – Фазовый портрет с нелинейным элементом зона нечувствительности

Устойчивый узел



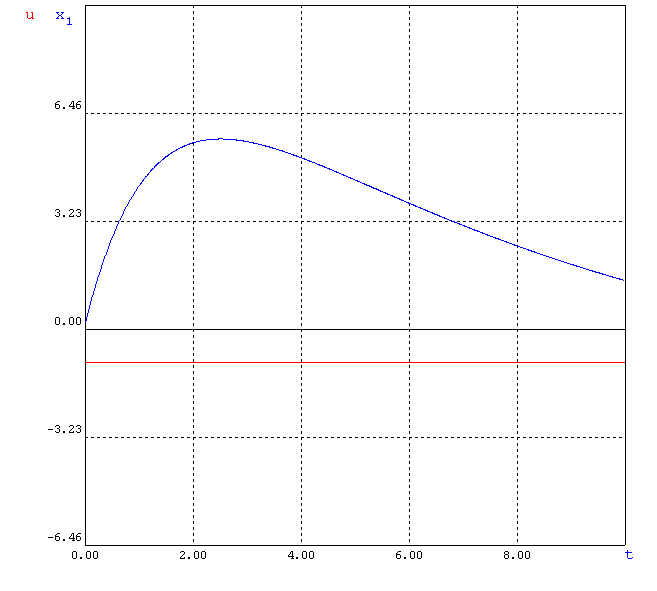
Рисунок 2.8 – Переходный процесс в системе с нелинейным элементом зона нечувствительности

Процесс во времени – апериодический.

---

2.2. Исследование скользящего режима и условий скачков

Рассмотрим следующую систему (рисунок 2.2.1):



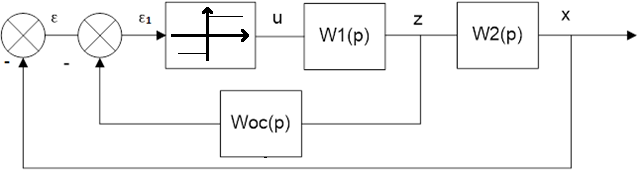
Рисунок 2.9 – Структурная схема исследуемой системы.

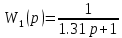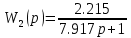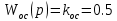В представленной выше системе присутствует местная обратная связь, наличие которой вызывает воздействие по производной на выходе нелинейного элемента, то есть на входе линейной части, что в свою очередь является причиной скачков фазовых траекторий на линиях переключения и, вследствие этого, скользящего режима.

Уравнение скачков:

---

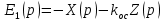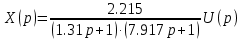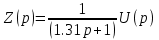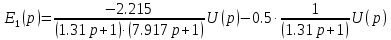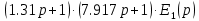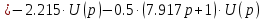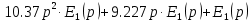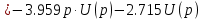В итоге получим следующее дифференциальное уравнение:

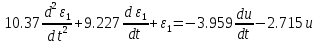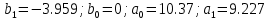Так как , значит скачка по координате 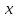нет.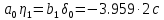

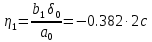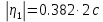– полосаскачка по скорости.

Уравнение линии переключения:

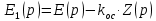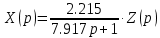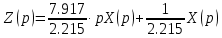Подставляем в верхнее уравнение и получаем следующее:

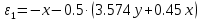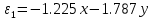Уравнение линии переключения зависит не только от типа нелинейного элемента, но и от дифференциального уравнения линейной части. В нашем случае нелинейный элемент – идеальное реле. У идеального реле линия переключения 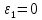. Тогда имеем следующее уравнение линии переключения:

---

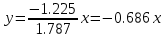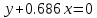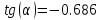– тангенс угла наклона линии переключения

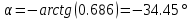– угол наклона линии переключения

Теперь найдем координаты полосы скользящего режима, исходя из полосы скачка по скорости и уравнения линии переключения.

Из полосы скачка по скорости найдем 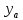и :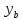

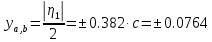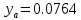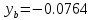Найдем координаты 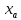и 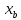из уравнения линии переключения:

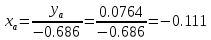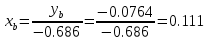Проверим найденные координаты точек А и В.

Точка А есть точка касания параболы 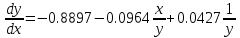с линией переключения 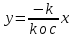, значит тангенс угла наклона касательной равен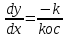



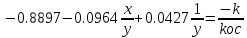
Следовательно

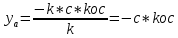
Очевидно, =

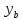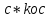
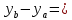
Полоса скользящего режима 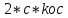, где 2с =

---