ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 185
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
– скачок статической характеристики идеального реле в момент переключения.
Теперь построим график линии переключения и выделим на нем отрезок скользящего режима.
скользящего режима.
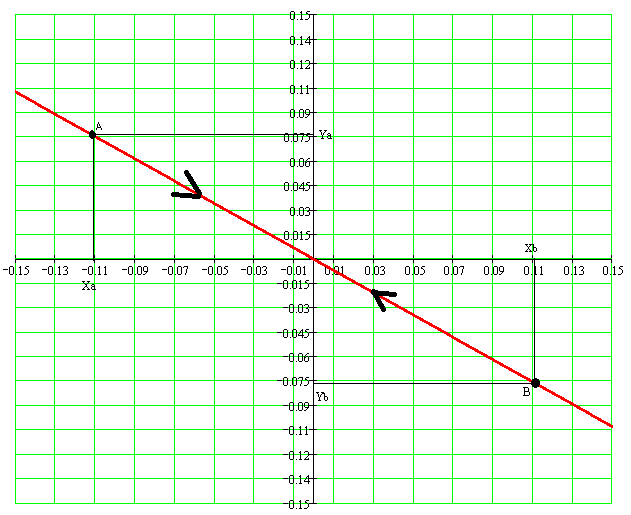
Рисунок 2.10 – График линии переключения с отрезком скользящего режима для идеального реле.
для идеального реле.
Найдем закон движения изображающей точки в полосе скользящего режима для идеального реле:
Теперь построим процесс во времени внутри граничных координат.
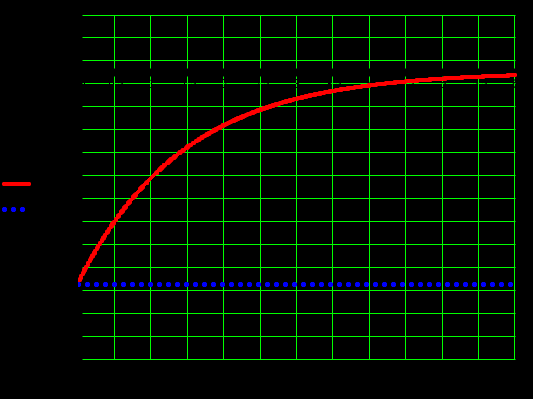
Рисунок 2.11 – Процесс во времени для точки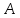 .
.
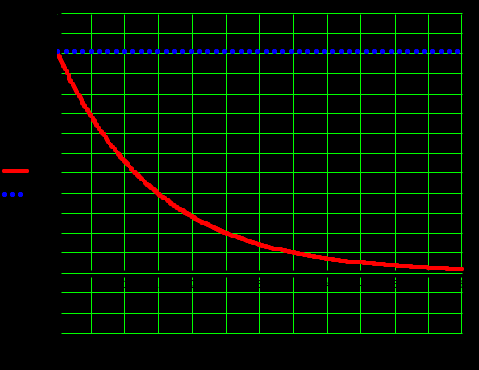
Рисунок 2.12– Процесс во времени для точки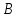 .
.
2.3 Расчёт автоколебаний (АК) методом гармонического баланса
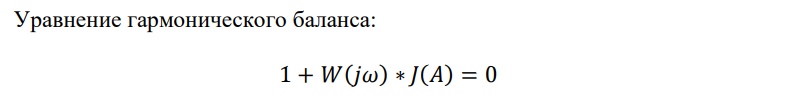
I) Идеальное реле

Рисунок 2.13 – Структурная схема замкнутой системы с нелинейным элементом идеальное реле
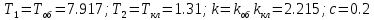
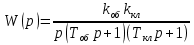
Строим график инверсной амплитудно-фазовой характеристики (АФХ):
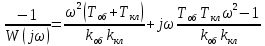
В Таблице 2.3.1 приведены значения действительной (Re) и мнимой (Im) частей функции инверсной АФХ в зависимости от значения частоты ω:
Таблица 2.3.1
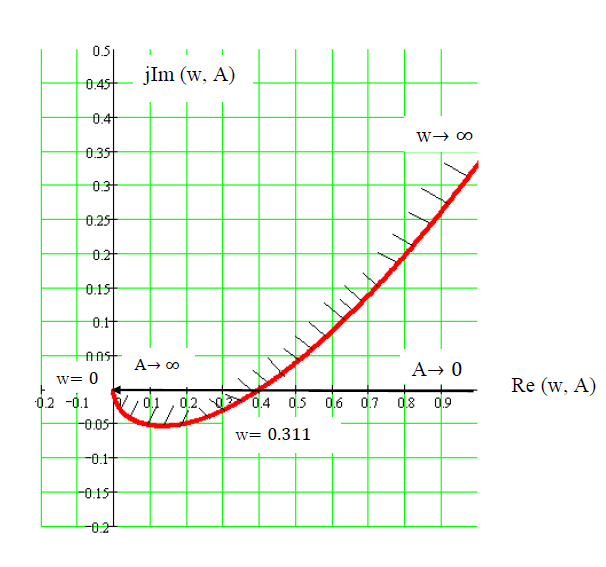
Рисунок 2.14 – Графическое решение уравнения гармонического баланса
Частота в точке пересечения ωАК = 0.311. Комплексный коэффициент усиления J(A) = 4c/(πA). Амплитуда 0.402 = 4c/(πAАК). Значит AАК = 0.633.
Проверка гипотезы фильтра.
1) Находим частоту пропускания
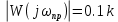
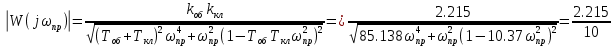
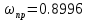
2) Гипотеза фильтра выполняется, если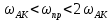
0.311 < 0.8996 < 0.622 - неверно
Гипотеза фильтра не подтвердилась, значит, автоколебаний нет. Подберём другие значения параметров Тоб и Ткл, чтобы выполнялась гипотеза фильтров.
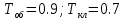
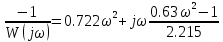
В Таблице 2.3.2 приведены значения действительной (Re) и мнимой (Im) частей функции инверсной АФХ в зависимости от значения частоты ω:
Таблица 2.3.2
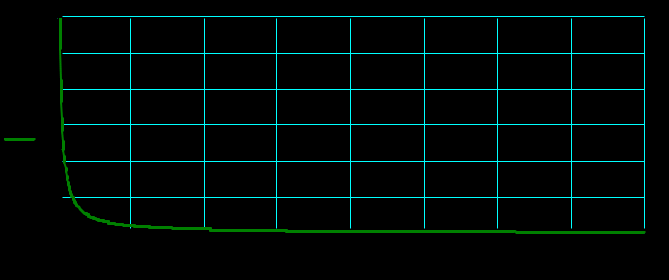
Рисунок 2.15 – График J(A)
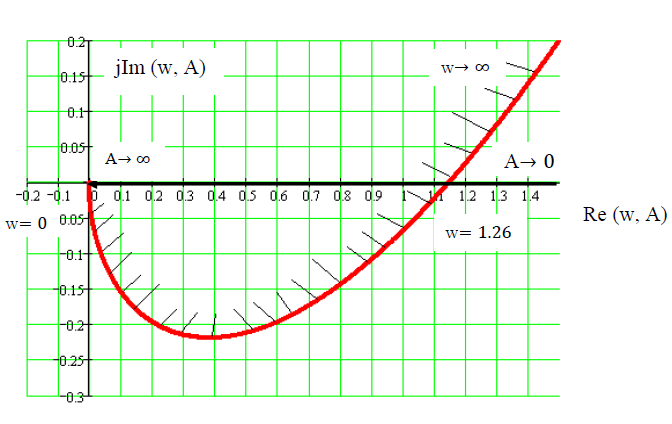 Рисунок 2.16 – Графическое решение уравнения гармонического баланса
Рисунок 2.16 – Графическое решение уравнения гармонического баланса
Частота в точке пересечения ωАК = 1.26. Комплексный коэффициент усиления J(A) = 4c/(πA). Амплитуда 1.146= 4c/(πAАК). Значит AАК = 0.222.
Проверка гипотезы фильтра.
1) Находим частоту пропускания
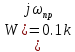
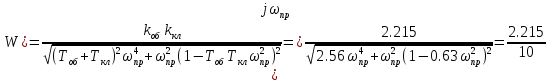
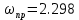
2) Гипотеза фильтров выполняется, если
1.26 < 2.298 < 2.52 верно
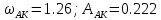
Переходный процесс выглядит следующим образом:
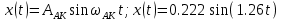
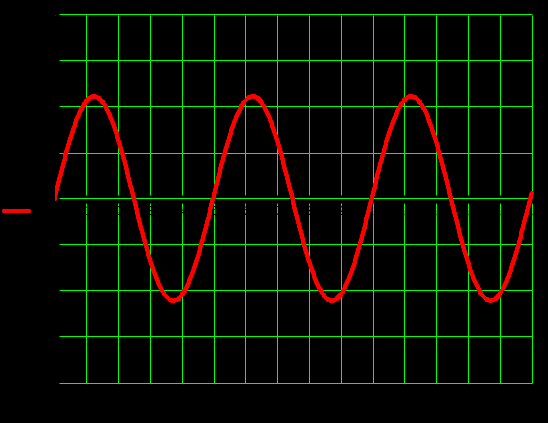
Рисунок 2.17 – Переходный процесс системы с нелинейным элементом идеальное реле
II) Зона нечувствительности

Рисунок 2.18 - Структурная схема замкнутой системы с нелинейным элементом зона нечувствительности
C=0.2; a=0.1.
Комплексная передаточная функция J(A) зоны нечувствительности:
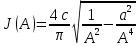
ωАК = 1.26 из предыдущего пункта
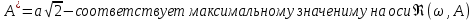
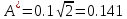
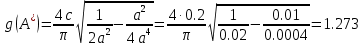
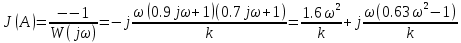
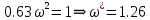
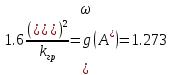
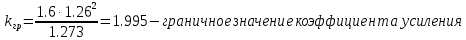
1)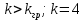
Автоколебания возможны.
Таблица 2.3.3
2)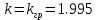
Граничный случай, автоколебаний нет:
Таблица 2.3.4
3)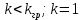
Автоколебания невозможны, т.к. нет пересечения с областью автоколебаний (уравнение гармонического баланса (ГБ) не имеет решения):
Таблица 2.3.5
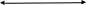
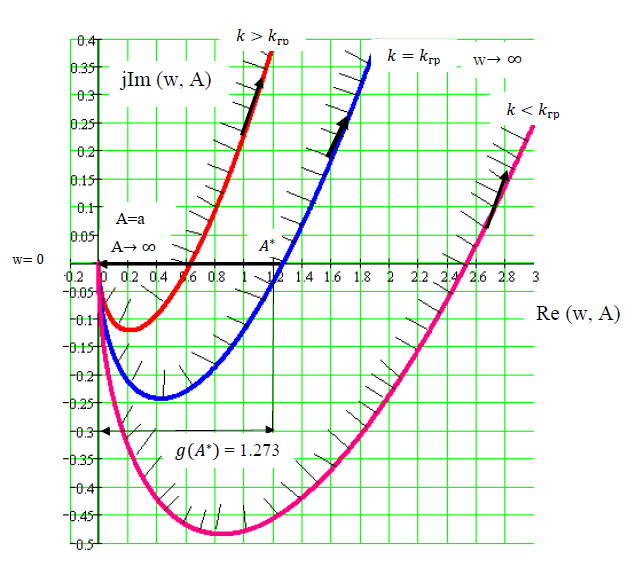 Рисунок 2.19 – Графическое решение уравнения гармонического баланса
Рисунок 2.19 – Графическое решение уравнения гармонического баланса
Найдём амплитуду устойчивых АК:
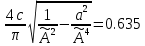
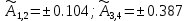
Отрицательные значения отбрасываем и берём большую амплитуду, т.к. при большей амплитуде график J(A) втекает в устойчивую область. Поэтому,
А* =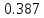 .
.
Решение уравнения ГБ
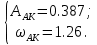
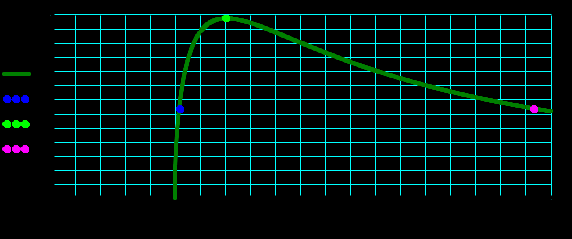
Рисунок 2.20 – График J(A)

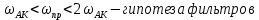
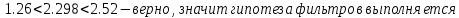
Переходный процесс выглядит следующим образом:
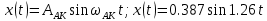
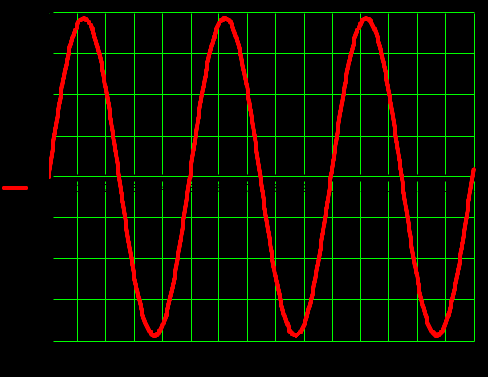
Рисунок 2.21 – Переходный процесс системы с нелинейным элементом зона нечувствительности
2.4 Исследование условий абсолютной устойчивости: сравнение результатов
Теперь построим график линии переключения и выделим на нем отрезок
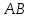 скользящего режима.
скользящего режима.
Рисунок 2.10 – График линии переключения с отрезком скользящего режима
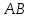 для идеального реле.
для идеального реле.Найдем закон движения изображающей точки в полосе скользящего режима для идеального реле:
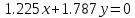 | |
| | |
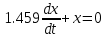 | |
| | |
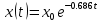 | |
Теперь построим процесс во времени внутри граничных координат.
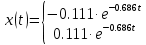 | |

Рисунок 2.11 – Процесс во времени для точки
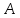 .
.
Рисунок 2.12– Процесс во времени для точки
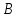 .
.2.3 Расчёт автоколебаний (АК) методом гармонического баланса
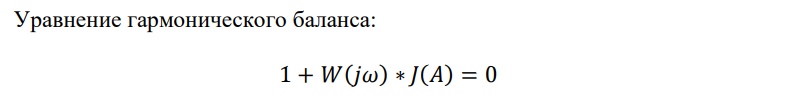
I) Идеальное реле

Рисунок 2.13 – Структурная схема замкнутой системы с нелинейным элементом идеальное реле
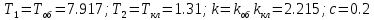
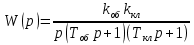
Строим график инверсной амплитудно-фазовой характеристики (АФХ):
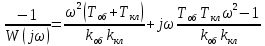
В Таблице 2.3.1 приведены значения действительной (Re) и мнимой (Im) частей функции инверсной АФХ в зависимости от значения частоты ω:
Таблица 2.3.1
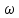 | 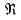 | 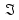 |
| 0 | 0 | 0 |
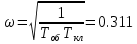 | 0.402 | 0 |
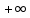 | 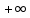 | 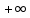 |

Рисунок 2.14 – Графическое решение уравнения гармонического баланса
Частота в точке пересечения ωАК = 0.311. Комплексный коэффициент усиления J(A) = 4c/(πA). Амплитуда 0.402 = 4c/(πAАК). Значит AАК = 0.633.
Проверка гипотезы фильтра.
1) Находим частоту пропускания
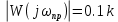
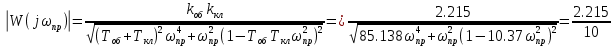
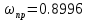
2) Гипотеза фильтра выполняется, если
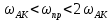
0.311 < 0.8996 < 0.622 - неверно
Гипотеза фильтра не подтвердилась, значит, автоколебаний нет. Подберём другие значения параметров Тоб и Ткл, чтобы выполнялась гипотеза фильтров.
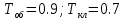
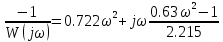
В Таблице 2.3.2 приведены значения действительной (Re) и мнимой (Im) частей функции инверсной АФХ в зависимости от значения частоты ω:
Таблица 2.3.2
 |  |  |
| 0 | 0 | 0 |
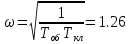 | 1.146 | 0 |
 |  |  |

Рисунок 2.15 – График J(A)
 Рисунок 2.16 – Графическое решение уравнения гармонического баланса
Рисунок 2.16 – Графическое решение уравнения гармонического балансаЧастота в точке пересечения ωАК = 1.26. Комплексный коэффициент усиления J(A) = 4c/(πA). Амплитуда 1.146= 4c/(πAАК). Значит AАК = 0.222.
Проверка гипотезы фильтра.
1) Находим частоту пропускания
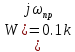
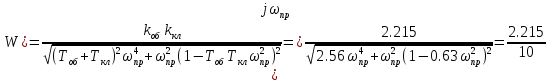
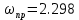
2) Гипотеза фильтров выполняется, если

1.26 < 2.298 < 2.52 верно
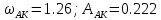
Переходный процесс выглядит следующим образом:
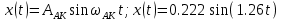

Рисунок 2.17 – Переходный процесс системы с нелинейным элементом идеальное реле
II) Зона нечувствительности

Рисунок 2.18 - Структурная схема замкнутой системы с нелинейным элементом зона нечувствительности
C=0.2; a=0.1.
Комплексная передаточная функция J(A) зоны нечувствительности:
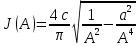
ωАК = 1.26 из предыдущего пункта
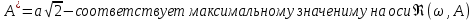
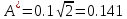
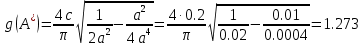
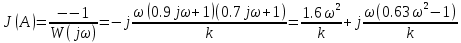
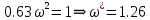
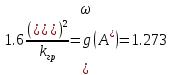
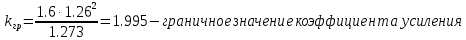
1)
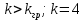
Автоколебания возможны.
Таблица 2.3.3
 |  |  |
| 0 | 0 | 0 |
| 1.26 | 0.635 | 0 |
 |  |  |
2)
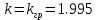
Граничный случай, автоколебаний нет:
Таблица 2.3.4
 |  |  |
| 0 | 0 | 0 |
| 1.26 | 1.273 | 0 |
 |  |  |
3)
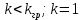
Автоколебания невозможны, т.к. нет пересечения с областью автоколебаний (уравнение гармонического баланса (ГБ) не имеет решения):
Таблица 2.3.5
 |  |  |
| 0 | 0 | 0 |
| 1.26 | 2.54 | 0 |
 |  |  |
 Рисунок 2.19 – Графическое решение уравнения гармонического баланса
Рисунок 2.19 – Графическое решение уравнения гармонического балансаНайдём амплитуду устойчивых АК:
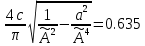
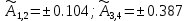
Отрицательные значения отбрасываем и берём большую амплитуду, т.к. при большей амплитуде график J(A) втекает в устойчивую область. Поэтому,
А* =
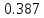 .
.Решение уравнения ГБ
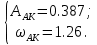

Рисунок 2.20 – График J(A)

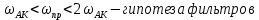
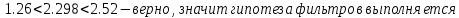
Переходный процесс выглядит следующим образом:
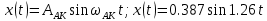

Рисунок 2.21 – Переходный процесс системы с нелинейным элементом зона нечувствительности
2.4 Исследование условий абсолютной устойчивости: сравнение результатов