ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 150
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.Представляется целесообразным заменить в полученной формуле момент инерции фигуры относительно линии пересечения поверхности жидкости со стенкой Jx через цент тяжести С параллельно поверхности жидкости, по известной формуле механики
.Тогда
. (I.10)Из полученной формулы видно, что центр давления D (рис. 3) лежит ниже центра тяжести С на величину
, называемую эксцентриситетом давления. Например, для прямоугольного щита координата центра давления lD равна:
(так как для прямоугольника
). Таким образом, точка приложения равнодействующей сил давления на прямоугольную стенку лежит ниже ее центра тяжести на 1/6 l.Равнодействующая сил давления на криволинейную стенку может быть определена суммированием сил давления на элементарные площадки, которые можно считать плоскими. Обычно задача определения равнодействующей давления на криволинейную стенку сводится к нахождению ее составляющих по координатным осям.
Определим суммарное давление жидкости на цилиндрическую поверхность АВ с горизонтальной образующей, которая направлена параллельно оси Oy (рис. 4).
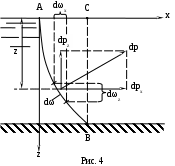
Для этого выделим на поверхности АВ элементарную площадку dω, погруженную под уровень жидкости на глубину z. Суммарное давление dP на эту площадку должно быть направлено по внутренней нормали к площадке и проходит через центр ее тяжести.
Если учитывать только избыточное гидростатическое давление, то суммарное давление определится по формуле dP = γz dω. Разложим это давление на две составляющих – на горизонтальную dPx и вертикальную dPz. Эти составляющие суммарного давления можно будет записать в следующем виде:
,
,где α – угол, составленный суммарным давлением с осью x.
Произведение
можно рассматривать как проекцию площадки dω на вертикальную плоскость dωz, а 
как проекцию площадки dω на горизонтальную плоскость dωx, то есть 
и 
. Подставляя эти выражения в проекцию суммарного давления на оси координат, будем иметь:
,
.Для того чтобы получить проекции суммарного давления жидкости на всю цилиндрическую поверхность АВ, проинтегрируем полученные выражения по указанной площади ω.
Тогда будем иметь:
,
.Рассмотрим выражение для горизонтальной составляющей суммарного давления
.
– есть статический момент площади вертикальной проекции цилиндрической поверхности относительно оси y, то есть 
, где zc – расстояние до центра тяжести вертикальной проекции криволинейной поверхности до свободной поверхности жидкости. Следовательно,
.Горизонтальная составляющая суммарного давления жидкости на цилиндрическую поверхность равна избыточному гидростатическому давлению: в центре тяжести проекции цилиндрической поверхности на вертикальную плоскость, умноженному на величину этой площади. Центр давления горизонтальной составляющей Рх будет определяться так же, как для суммарного давления на вертикальную плоскость
.
В данном случае I0 – момент инерции цилиндрической поверхности на вертикальную плоскость относительно центральной горизонтальной оси.
Рассмотрим выражение для вертикальной составляющей суммарного давления жидкости на цилиндрическую поверхность
, 
– есть не что иное, как объем призмы АВС, или иначе объем тела давления W, то есть
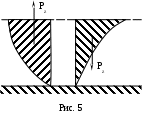
.Телом давления называется объем, ограниченный цилиндрической поверхностью, вертикальной плоскостью, проходящей через нижнюю образующую цилиндрической поверхности, и горизонтальной плоскостью, совпадающей со свободной поверхностью жидкости АС (или ее продолжением).
Таким образом, вертикальная составляющая суммарного давления жидкости на цилиндрическую поверхность Pz равна весу жидкости в объеме тела давления. Тело давления может быть фиктивным, если оно не заполнено жидкость a) и действительным, если оно жидкостью заполнено b) (рис. 5).
Полная величина суммарного давления жидкости на цилиндрическую поверхность может быть выражена геометрической суммой сил Px и Pz и определена по формуле
. (I.11)О
бе составляющие Px, Pz и их равнодействующая P должны иметь общую точку пересечения. Угол наклона равнодействующей P к горизонту α определится из выражения 
. Точка приложения полной силы давления Р к криволинейной поверхности находится в месте пересечения линии действия силы Р, проходящей через точку, с криволинейной поверхностью.Тема II. Основные понятия и уравнения гидродинамики
2.1. Основные определения кинематики жидкости.
Неразрывность
А. Основные определения. Из предыдущего известно, что состояние какого-либо объема покоящейся жидкости полностью определяется величинами внутренних напряжений (гидростатических давлений) в отдельных его точках, возникающих в результате воздействия на жидкость внешних сил. Для характеристики состояния движущейся жидкости недостаточно знать только распределение давлений. Необходимо знать также, с какими скоростями движется жидкость в различных точках, то есть задачей гидродинамики является определение скоростей и давлений жидкости в различных точках потока и в различные моменты времени t. В общем случае вектор скорости u и давление p являются функциями четырех переменных:
, 
.Если скорость и давление в любой фиксированной точке потока остаются неизменными во времени (т. е. являются функциями только координат х, у, z), то течение называется установившимся. Пример установившегося течения – истечение жидкости из бака под постоянным напором. Если скорость и давление меняются со временем, то течение – неустановившееся. Например, если при истечении из бака убыль жидкости не восполняется, то напор, скорость и давление в любой точке постепенно уменьшаются, это течение неустановившееся.
Мгновенную картину течения наглядно представляют линии тока (рис. 6, а). В каждой точке линии тока вектор скорости направлен по касательной к ней. При установившемся течении линии тока совпадают с траекториями частиц, при неустановившемся течении они могут не совпадать.
Е
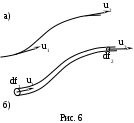сли провести линии тока через все точки элементарно-малого контура, то образованная ими поверхность ограничит элементарную струйку (рис. 6, б). В элементарной струйке жидкость течет, не смешиваясь с соседними объемами, так как, по определению, векторы скорости направлены по касательной к ее поверхности. Площадь сечения струйки dS
выбирают достаточно малой для того, чтобы вектор скорости u оставался в этом сечении неизменным по величине.
Объем жидкости, протекающей через сечение струйки в единицу времени, называют элементарным расходом dQ. Он равен произведению длины вектора скорости на площадь сечения струйки
. (II.1)Размерность расхода – м3/сек.
Рассматривая поток жидкости, такой, например, как в трубе или канале, допустимо считать, что он состоит из большого числа элементарных струек. В этом случае сечение потока (в гидравлике его называют «живым сечением») равно сумме сечений элементарных струек. Расход потока есть сумма расходов струек, в пределе – интеграл по площади сечения:
. (II.2)При известном расходе Q легко определить среднюю скорость потока V в данном сечении:
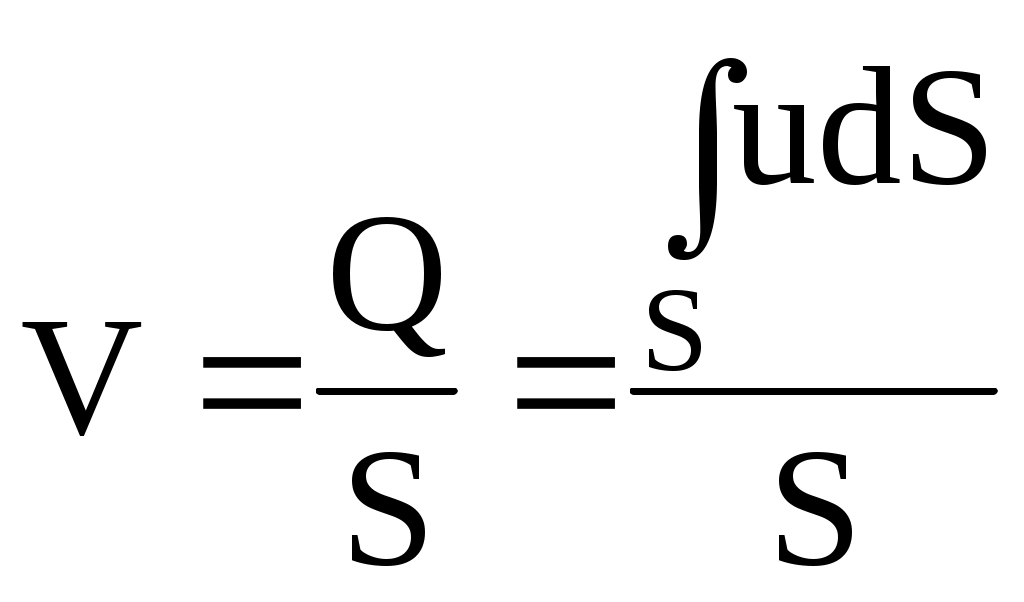. (II.3)Для характеристики торможения потока твердыми стенками кроме сечения S в гидравлике вводятся еще понятия смоченного периметра χ – периметр сечения в пределах соприкосновения с твердыми стенками трубы или канала, и гидравлического радиуса R, причем
. (II.4)Размерность смоченного периметра и гидравлического радиуса – м.
Как видно из выражения (II.4), гидравлический радиус характеризует компактность сечения потока. Для круглой трубы радиуса r, например, гидравлический радиус
, если d – диаметр трубы, то 
.Если в потоке между какими-нибудь двумя его сечениями количество жидкости не пополняется извне и не убывает (нет источников и стоков), то масса протекающей через эти два сечения жидкости сохраняется неизменной. Математически этот принцип выражается уравнением неразрывности (это название подчеркивает, что в рассматриваемых сечениях поток сплошной, не содержит полостей и разрывов).
Наиболее просто записывается уравнение неразрывности для установившегося одномерного течения, в котором скорость меняется только в направлении одной продольной координаты. Примерами одномерного течения являются элементарная струйка, движение в трубе и канале. Для элементарной струйки несжимаемой жидкости принцип сохранения массы выражается через постоянство объемного расхода (II. 1) в струйке (рис. 6, б):