ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 542
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Непрерывная величина задана плотностью
Н
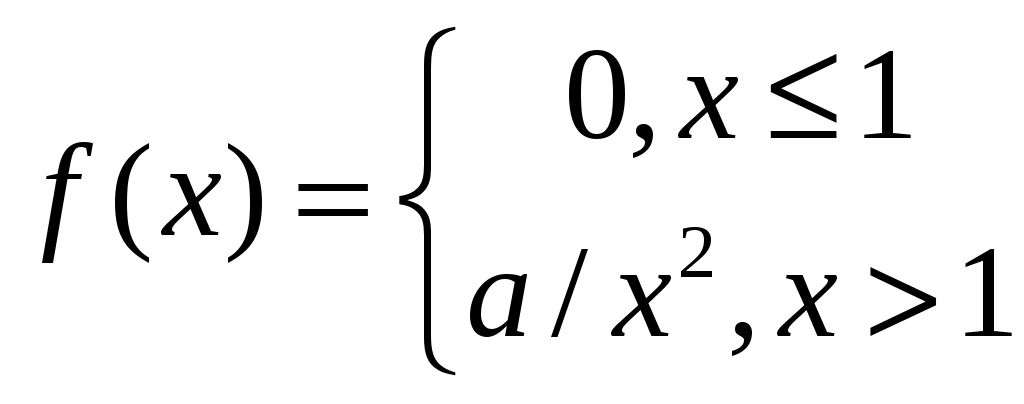
айти коэффициент а, функцию распределения, вероятность события {2<X<3}.
-
Ошибки прибора распределены нормально с нулевым мат.ожиданием и ско, равным 3. Какова вероятность того, что ошибка по модулю превзойдет 6? Какова вероятность того, что это произойдет лишь два раза в пяти измерениях?
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.99
-
Вероятность одного попадания в цель при залпе из двух орудий равна 0,38. Какова вероятность поражения цели первым орудием, если известно, что для второго орудия эта вероятность равна 0,8 ?
-
Оцените вероятность того, что четырехзначный номер первой встречной машины не содержит а) цифры 5; б) содержит две и более пятерки.
-
В кузове 768 арбузов. Каждый может оказаться неспелым с вероятностью 0,25. С какой вероятностью число спелых арбузов в партии лежит в пределах от 564 до 600? Более 700?
-
Третья часть только одной из трех партий является второсортной. Деталь, взятая из какой-то партии, оказалась первосортной. Какова вероятность того, что она из партии, в которой есть второсортные?
-
По некоторой цели производится стрельба пятью ракетами. Вероятность попадания у каждой ракеты 0,7. Найти числовые характеристики случайной величины Х – число попаданий.
-
Детали от двух заводов поступают на сборку. Количество деталей от второго в три раза больше. Детали перемешаны. Вероятность брака на первом заводе 0,01, на втором – 0,02.
Наугад берем две детали. Обе оказались бракованными. Какова вероятность того, что они от второго завода?
-
Рост человека в данной местности есть нормальная с.в. с m=165 и =7. Какова вероятность того, что наудачу выбранный человек имеет рост от 155 до 170 см? Выше, чем 182 см? В каком диапазоне равных отклонений от ожидаемого находится рост с вероятностью 0,95?
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.98
-
Двое бросают монету по очереди. Выигрывает тот, у кого раньше появится герб. Найти вероятности выигрыша каждого из игроков.
-
Отдел технического контроля проверяет изделия. Вероятность брака – 0,1. Найти вероятность того, что из трех проверенных лишь одно окажется бракованным. Какова вероятность того, что хотя бы одно будет бракованным?
-
Радиостанция состоит из трех блоков, которые могут выйти из строя с вероятностями 0,1 , 0,2 и 0,4. Определить вероятности того, что
из строя вышел один из блоков;
из строя вышли 2-й и 3-й блоки;
отказал хотя бы один блок.
-
В помещении 5 ламп. Каждая перегорает в течение года с вероятностью 0,2. Найти наиболее вероятное число работающих ламп в конце года.
-
Третья часть только одной из трех партий является второсортной. Деталь, взятая из какой-то партии, оказалась первосортной. Какова вероятность того, что она из партии, в которой есть второсортные.
-
По некоторой цели производится стрельба пятью ракетами. Вероятность попадания у каждой ракеты 0,7. Найти числовые характеристики случайной величины Х – число попаданий.
-
Ошибка в изготовлении детали нормальна с с m=0,1мм и σ=0,15мм. Если ошибка по модулю не превосходит 0,3мм, то деталь можно использовать. Изготовлено 7 деталей.
Найти ожидаемое число годных. Какова вероятность того, что негодных будет более половины?
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.99
-
В первой урне 5 белых, 11 черных и 8 красных шаров, а во второй 19 белых, 8 черных и 6 красных. Из каждой урны извлекают по одному шару. Какова вероятность того, что шары будут одного цвета? Какова вероятность появления разноцветных шаров в этом же эксперименте? Какова вероятность, что оба шара черные, если известно, что первый шар черный?
-
В городе три библиотеки. Вероятность того, что нужная книга есть в библиотеке равна 0,5, а вероятность того, что она при этом не выдана равна 0,6. Найти вероятность того, что мы получим книгу.
-
В колоде 52 карты. Какова вероятность:
а)вытянув две карты получить сначала туза, а потом короля?
б)вытянув две карты, получить туза и короля?
в)вытянув пять карт получить не менее двух тузов?
г)вытянув одну карту получить либо туза, либо пики?
-
В ящике 3 пары совершенно одинаковых ботинок. Вынимаем наугад по одному ботинку пока не составится пара. Найти закон распределения и числовые характеристики с.в..Х – число вынутых ботинок.
-
В коробке 3 новых и 3 использованных теннисных мяча. Наудачу берем два, играем и возвращаем в коробку. Какова вероятность в следующий раз вынуть два новых мяча?
-
Интервал времени между отказами системы имеет функцию распределения F(t)=F(t)=1-e-t,t>0. Определить плотность распределения и числовые характеристики. Определить вероятность того, что интервал между отказами превысит математическое ожидание.
-
Ошибки прибора распределены нормально с нулевым мат.ожиданием и ско, равным 3. Какова вероятность того, что ошибка по модулю превзойдет 6? Какова вероятность того, что это произойдет лишь два раза в пяти измерениях?
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар100
-
На шахматную доску случайным образом ставят две ладьи. Какова вероятность того, что они «бьют» друг друга? То же для случая двух слонов.
-
Бросаем две кости. Какова вероятность того, что сумма значений равна7, если известно. Что сумма нечетная?
-
Партия из 100 деталей подвергается выборочному контролю. Для этого берут наугад 5 штук и, если среди них есть хотя бы одна дефектная, то бракуем всю партию. Какова вероятность этого события, если на самом деле в партии 5 дефектных деталей? Как изменится эта вероятность, если после проверки каждая деталь возвращается в партию и перемешивается?
-
Отрезок разделен не три равные части. На отрезок наугад бросают три точки. Какова вероятность того, что на каждую из частей попадет по одной точке? Какова вероятность того, что все точки попадут на одну из частей отрезка?
-
В первом ящике 5 годных и 7 дефектных деталей, а во втором 9 годных и 3 дефектные. Детали смешивают и извлекают наугад две. Они оказались дефектными. Какова вероятность того, что они из второго ящика?
-
По цели производится 4 выстрела. Вероятность попадания при этом растет так – 0,2 , 0,4 , 0,6 , 0,7. Найти закон распределения с.в.Х – число попаданий. Найти вероятность того. что Х 1.
-
Ошибки прибора распределены нормально с нулевым мат.ожиданием и ско, равным 3. Какова вероятность того, что ошибка по модулю превзойдет 6? Какова вероятность того, что это произойдет лишь три раза в пяти измерениях?
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.101
1.Вероятность одного попадания в цель при залпе из двух орудий равна 0,38. Найти вероятность поражения цели при одном выстреле первым орудием, если для второго орудия эта вероятность равна 0,8.
2.Бросаем две кости. Какова вероятность того, что сумма значений равна 8, если известно,что сумма больше или равна 7?
3.В урне 9 белых и 4 черных шара. Извлекаем 3 шара. Какова вероятность того, что третий будет черным? Какова вероятность того, что третий будет черным, если известно, что первые два разные?
4.Из пачки в десять билетов выигрышными являются два. Наугад вынимаем 5 билетов. Какова вероятность того, что среди них 1 выигрышный? То же, но при возвращении каждого билета обратно в пачку и перемешивании.
5.Оцените вероятность того, что четырехзначный номер первой встречной машины не содержит а) цифры 5; б) содержит две и более пятерки.