Файл: Сборник работ для суммативного оценивания по алгебре и началам анализа 11 класс.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 4605
Скачиваний: 247
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «СТЕПЕНИ И КОРНИ. СТЕПЕННАЯ ФУНКЦИЯ»
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА»
7. Постройте сечение многогранника плоскостью, проходящей через точки Е, F и T. Опишите кратко построение сечения.
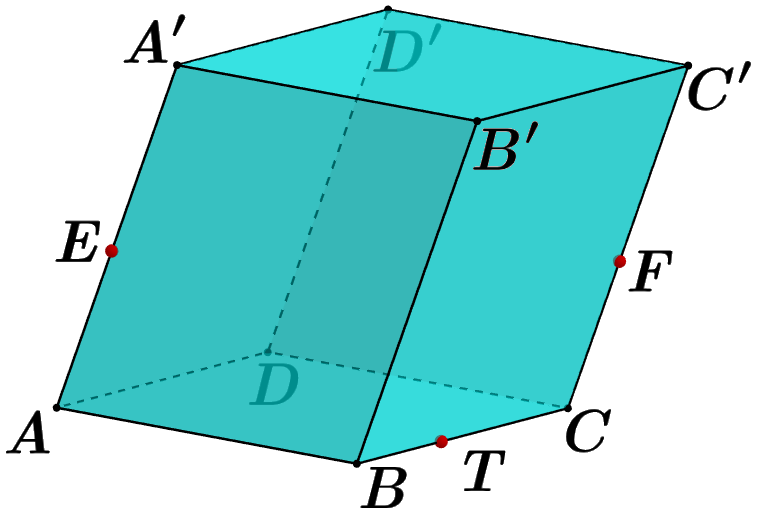
Схема выставления баллов
| № | Ответ | Балл | Дополнительная информация |
| 1 | В | 1 | |
| 2 | Строна основания пирамиды равна 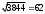 (м) (м) | 1 | |
| Апофема вычисляется по теореме Пифагора из прямоугольного треугольника с катетами 62м и 31м 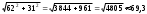 (м) (м) | 1 | | |
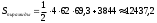 м² м² | 1 | | |
| 3 | 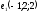 , , 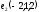 - направляющие векторы заданных прямых - направляющие векторы заданных прямых | 1 | Принимаются другие обозначения |
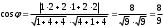 | 1 | | |
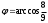 | 1 | | |
| 4 | 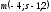 , , 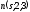 - направляющие векторы прямых m и n. - направляющие векторы прямых m и n. | 1 | Принимаются другие обозначения |
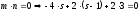 | 1 | | |
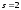 | 1 | | |
| 5 | 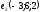 направляющий вектор прямой направляющий вектор прямой  | 1 | |
| Записано каноническое уравнение прямой  , проходящей через точку , проходящей через точку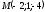 параллельно вектору параллельно вектору 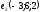 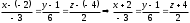 | 1 | | |
| Записано параметрическое уравнение прямой  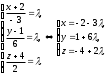 | 1 | Принимаются другие обозначения | |
| 6 | 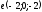 - направляющий вектор прямой - направляющий вектор прямой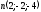 - вектор нормали плоскости - вектор нормали плоскости | 1 | |
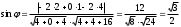 | 1 | | |
 | 1 | | |
| 7 | Проведена прямая FT так, что 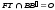 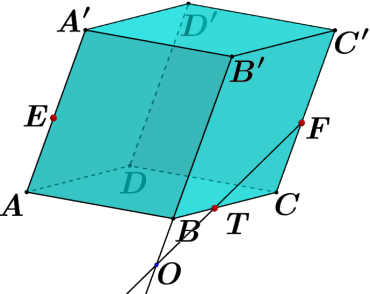 | 1 | |
| Проведена прямая ЕО так, что 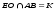 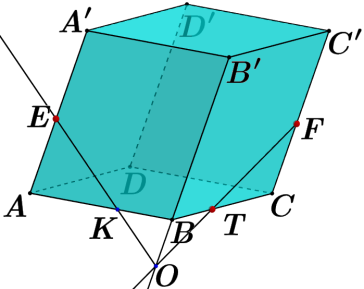 | 1 | | |
| Проведена прямая 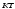 так, что так, что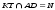 , ,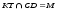 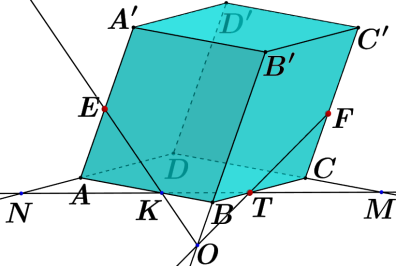 | 1 | | |
| Проведены прямые EN и FM так, что 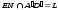 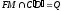 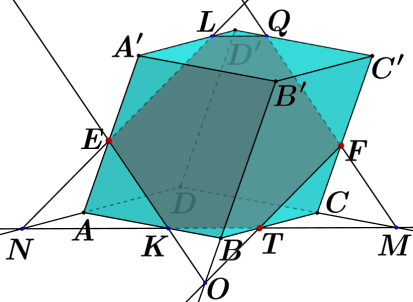 ELQFTK – искомое сечение | 1 | | |
| Итого: | 20 | | |
4 ВАРИАНТ
| Разбаловка заданий работы | |||||||
| № задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Количество баллов | 1 | 3 | 3 | 3 | 3 | 3 | 4 |
| итого | 20 баллов | ||||||
1. В правильной усечённой шестиугольной пирамиде стороны основания равны а и b, а апофема равна k. Найдите площадь боковой поверхности усечённой пирамиды.
А)
 ;
;В)
 ;
;С)
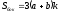 ;
;D)
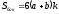 .
.2. В Париже большая стеклянная «Пирамида Лувра» имеет форму правильной четырехугольной пирамиды высотой 21,6м и площадью основания 1225м². Найдите площадь полной поверхности пирамиды (ответ округлите до десятых).

3. Найдите угол между прямыми, заданными уравнениями
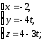 и
и 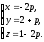
4. Прямые m и n заданы уравнениями
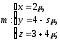 и
и 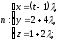 .
. Найдите значение s и t, при котором прямые m и n параллельны.
5. Составьте параметрическое уравнение прямой
 , проходящей через точки
, проходящей через точки 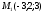 и
и 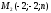 и перпендикулярно прямой
и перпендикулярно прямой 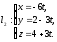
6. Найдите угол между прямой
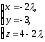 и плоскостью
и плоскостью 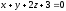 .
. 7. Постройте сечение многогранника плоскостью, проходящей через точки Е, F и T. Опишите кратко построение сечения.
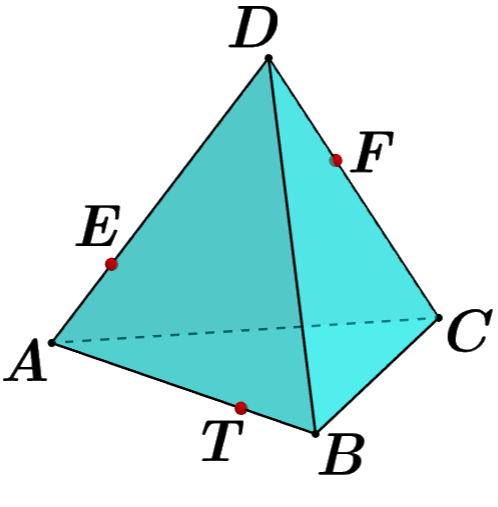
Схема выставления баллов
| № | Ответ | Балл | Дополнительная информация |
| 1 | С | 1 | |
| 2 | Строна основания пирамиды равна 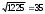 (м) (м) | 1 | |
| Апофема вычисляется по теореме Пифагора из прямоугольного треугольника с катетами 21,6м и 17,5м 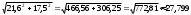 (м) (м) | 1 | | |
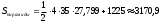 м² м² | 1 | | |
| 3 | 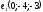 , , 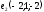 - направляющие векторы заданных прямых - направляющие векторы заданных прямых | 1 | Принимаются другие обозначения |
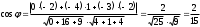 | 1 | | |
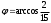 | 1 | | |
| 4 | 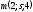 , , 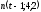 - направляющие векторы прямых m и n. - направляющие векторы прямых m и n. | 1 | Принимаются другие обозначения |
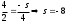 | 1 | | |
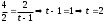 | 1 | | |
| 5 | 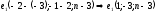 направляющий вектор прямой направляющий вектор прямой  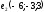 направляющий вектор прямой направляющий вектор прямой  | 1 | |
| Выполнено условие перпендикулярных прямых  и и  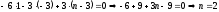 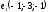 | 1 | | |
| Записано параметрическое уравнение прямой  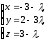 | 1 | Принимаются другие обозначения | |
| 6 |  - направляющий вектор прямой - направляющий вектор прямой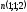 - вектор нормали плоскости - вектор нормали плоскости | 1 | |
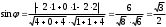 | 1 | | |
 | 1 | | |
| 7 | Проведена прямая EF так, что 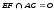 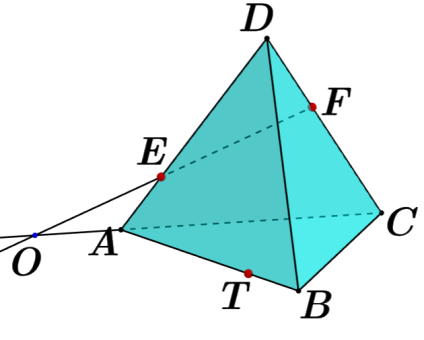 | 1 | |
| Проведена прямая ОТ так, что 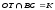 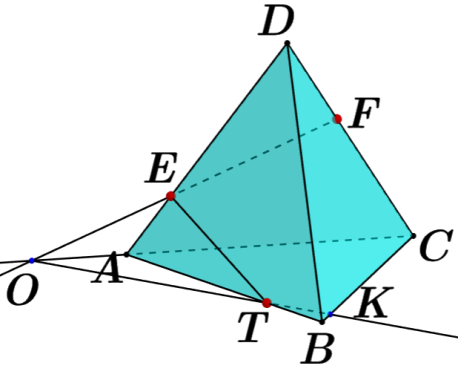 | 1 | | |
| Проведена прямая 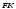  | 1 | | |
| EFKT – искомое сечение 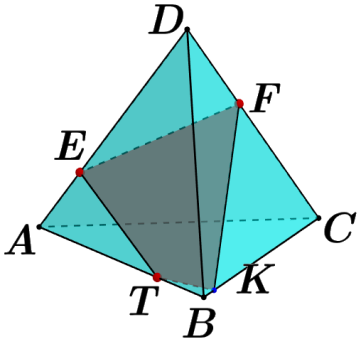 | 1 | | |
| Итого: | 20 | | |
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 3 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 3 четверть
Продолжительность - 40 минут
Количество баллов - 20
Типы заданий:
КО - задания, требующие краткого ответа;
РО - задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 5 заданий, включающих вопросы с кратким и развернутым ответами.
В вопросах, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.
В вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов.Характеристика заданий суммативного оценивания
| Раздел | Проверяемая цель | Уровень мыслительных навыков | Кол. заданий* | № задания* | Тип задани я* | Время на выполнение, мин* | Балл* | Балл за раздел |
| Тела вращения и их элементы | 11.3.4 - выводить формулы площади боковой и полной поверхности цилиндра и применять их при решении задач | Применение | 1 | 5 | РО | 8 мин | 5 | 20 |
| 11.3.5 - решать задачи на нахождение элементов тел вращения (цилиндра, конуса, усеченного конуса, шара) | Применение | 1 | 2 | РО | 10 мин | 4 | ||
| 11.3.6 - выводить формулы площади боковой и полной поверхности конуса и применять их при решении задач | Применение | 1 | 1 а / b | КО/РО | 8 мин | 4 | ||
| 11.3.7 - выводить формулы площади боковой и полной поверхности усеченного конуса и применять их при решении задач | Применение | 1 | 4 | РО | 8 мин | 3 | ||
| 11.1.10 - знать определение сферы, шара; уметь изображать их на плоскости | Знание и понимание | 1 | 3 | КО/РО | 2 мин | 1 | ||
| 11.3.10 - решать задачи, связанные с сечениями шара и сферы плоскостью | Применение | 4 мин | 3 | |||||
| ИТОГО: | | | 5 | | | 40 мин | 20 | 20 |