Файл: Дрістер жинаы (15 саат) etn (II) 2216 Электр техниканы теориялы негіздері (II).doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 160
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
< 0. (4.5а)
Абсолюттік шамасы бойынша | 1 | < |
1 | < |  2 |. Бұндай режим апериодтықдеп аталады, өйткені ток пен кернеу, өзінің бағытын өзгертпей, қалыптасқан режимге қарай ұмтылады;
2 |. Бұндай режим апериодтықдеп аталады, өйткені ток пен кернеу, өзінің бағытын өзгертпей, қалыптасқан режимге қарай ұмтылады;
б)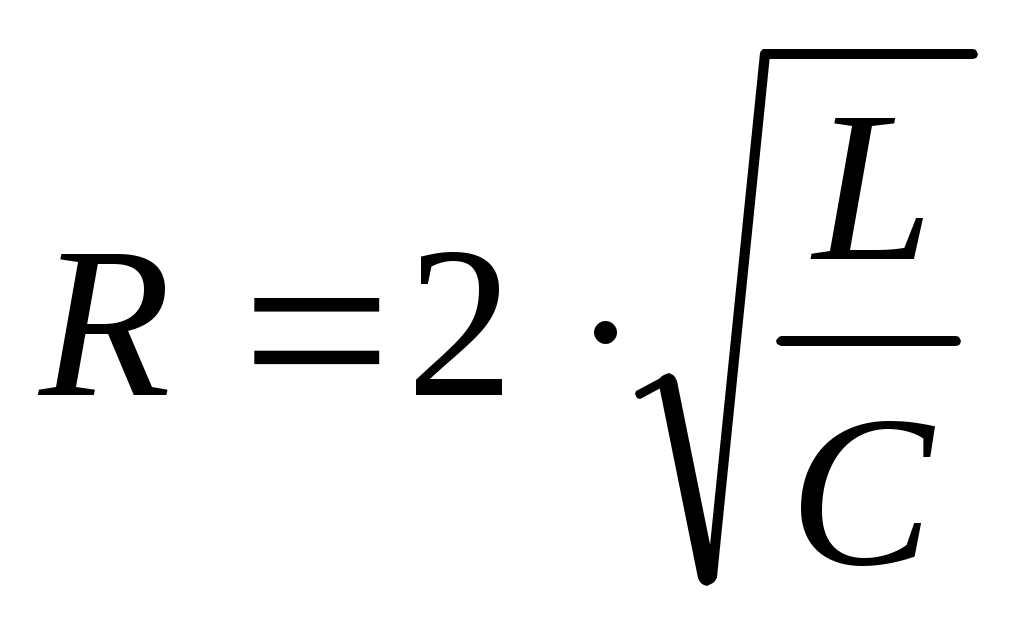 . Бұл шарттың орындалуы кезінде және теңдеу түбірлері бұл жағдайда да нақты, теріс таңбалы сандар болады:
. Бұл шарттың орындалуы кезінде және теңдеу түбірлері бұл жағдайда да нақты, теріс таңбалы сандар болады: 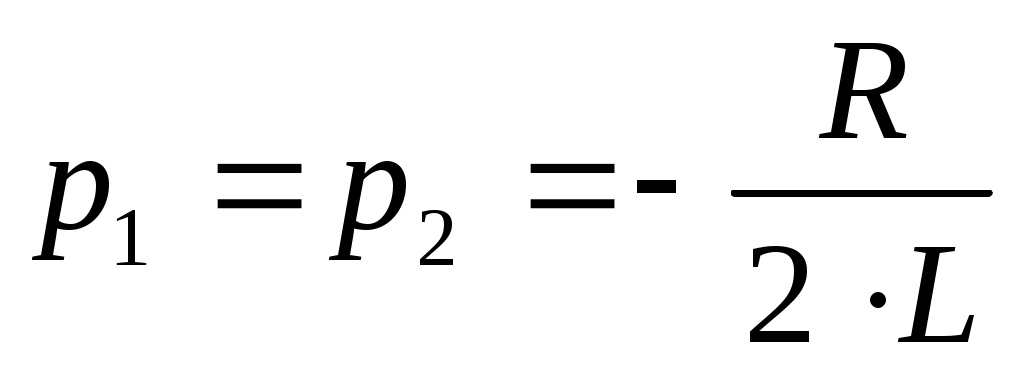 . Бұл жағдайда
. Бұл жағдайда 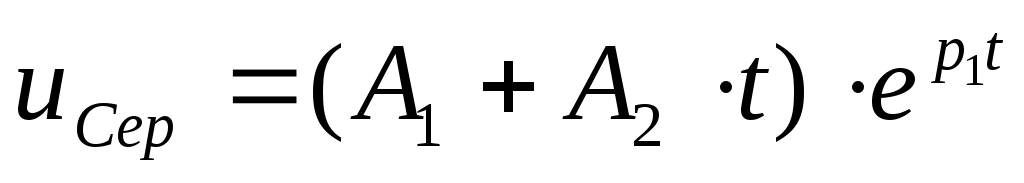 . (4.6)
. (4.6)
Бұл режим критикалық деп аталады.
в) <
< 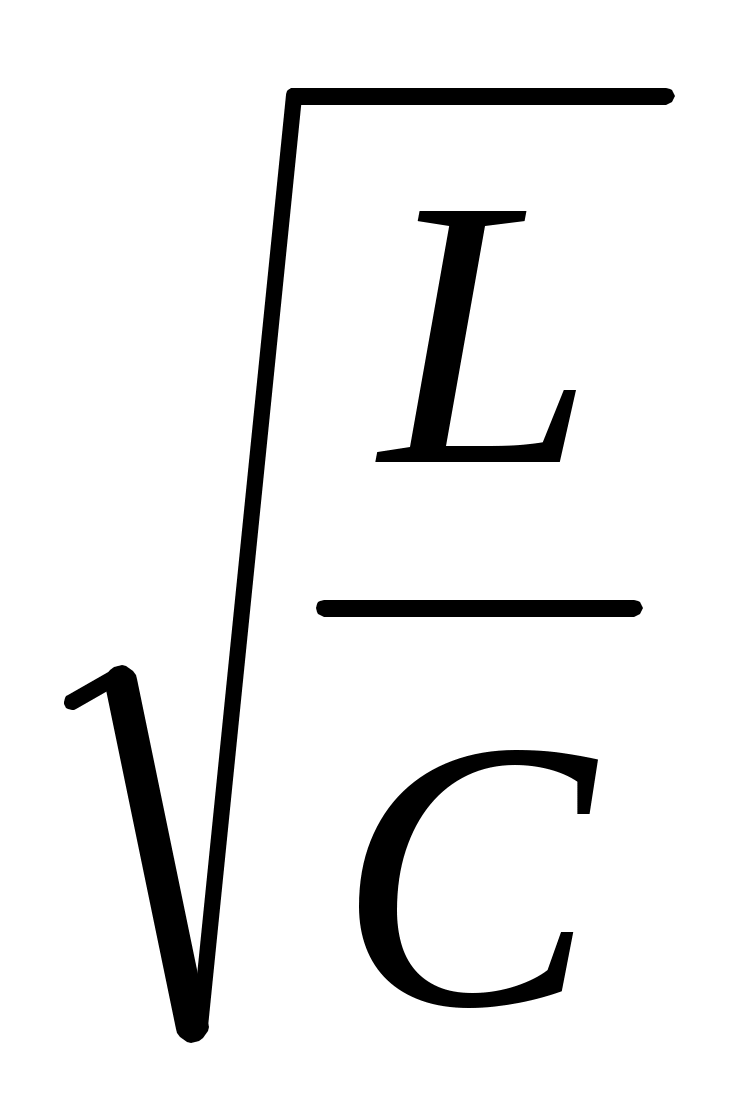 . Бұл жағдайда теңдеу түбірлері
. Бұл жағдайда теңдеу түбірлері 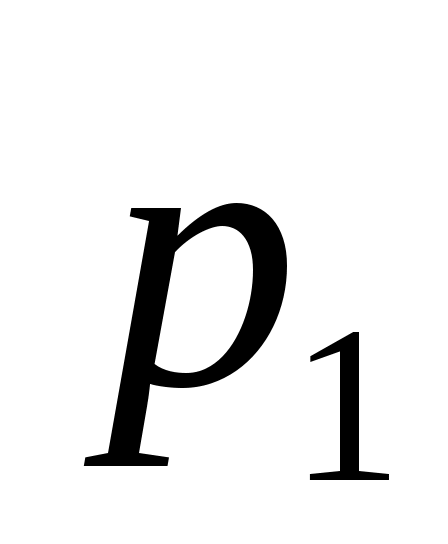 мен
мен 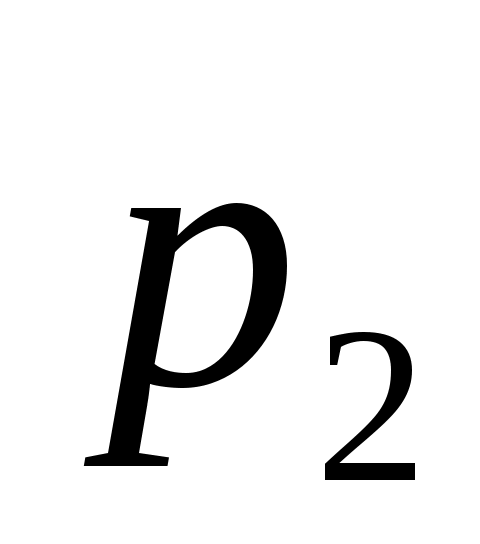 , нақты бөлігі теріс таңбалы, кешенді-сыбайлас мәнді шамалар болады:
, нақты бөлігі теріс таңбалы, кешенді-сыбайлас мәнді шамалар болады:
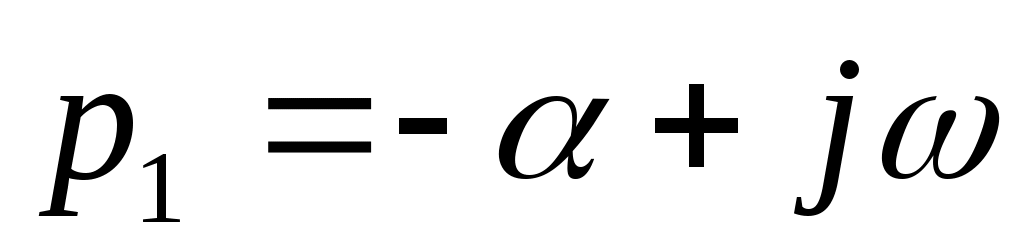 ;
; 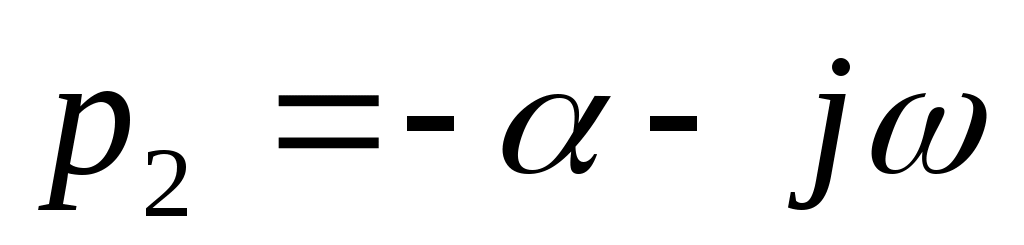 , (4.7)
, (4.7)
мұндағы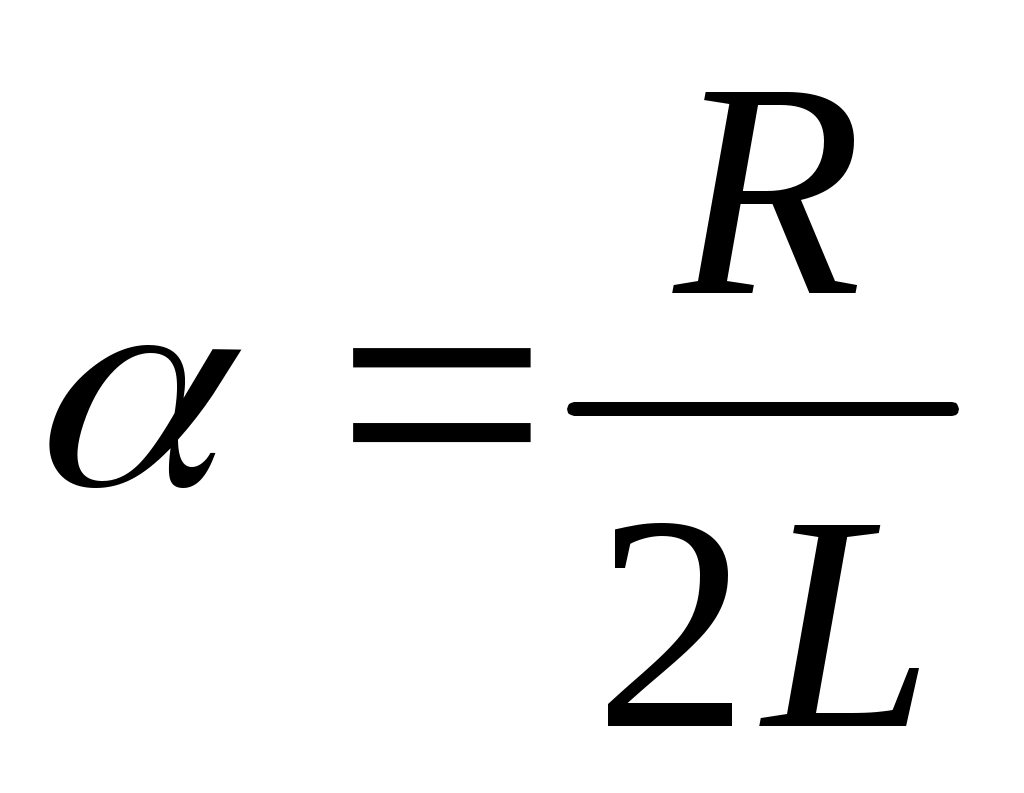 – сөну коэффициенті;
– сөну коэффициенті;
 =
= 
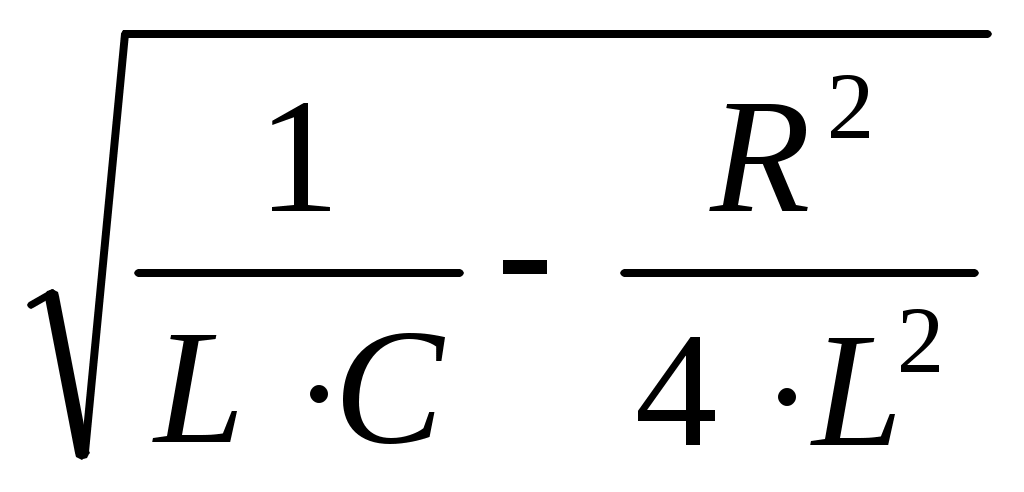
 - меншікті тербелістердің бұрыштық жиілігі.
- меншікті тербелістердің бұрыштық жиілігі.
Бұндай режим периодтық немесе тербелмелі деп аталады. Бұл жерде орауыш пен конденсатор арасында көп мөлшердегі энергия алмасуы жүріп өтеді: энергия бірде магниттік өріске (тоқ өскен кезде), бірде электр өрісіне (конденсатордағы кернеу өскенде) ауысып құйылатындай болады.
Интегралдау тұрақтылары бастапқы шарттардан анықталады.
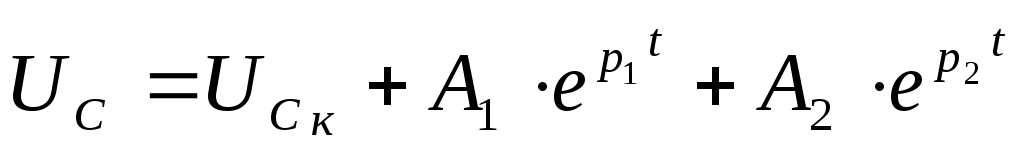 , (4.8)
, (4.8)
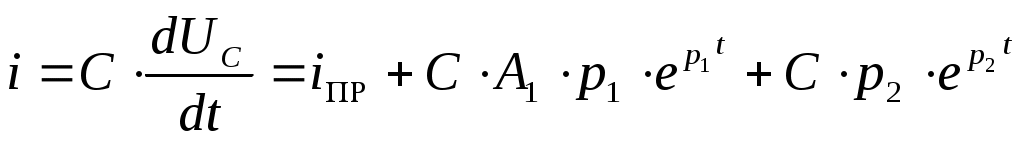
, (4.9)
 кезінде:
кезінде: 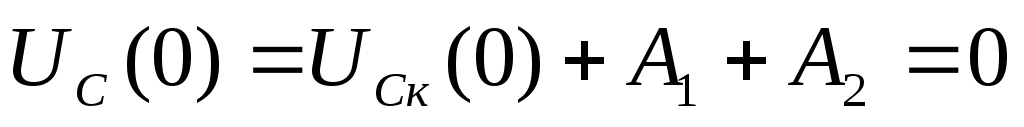 ,
,
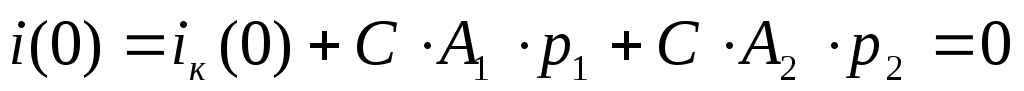 . (4.10)
. (4.10)
(4.10) теңдеулерінен және
және  оңай анықталады.
оңай анықталады.
№5 дәріс 5. Классикалық әдіспен өтпелі кезеңдерді есептеудің жалпы жағдайы.
Дәрістің мақсаты: тармақталған тізбектердегі өтпелі кезеңдерді классикалық әдіспен және тізбектің кез келген кернеу көзіне қосылуы кезіндегі есептеулерді меңгеру.
Берілген есеп, тоқтар мен кернеулердің лездік мәндері үшін Кирхгоф заңдары бойынша құрастырылған теңдеулер көмегімен шешіледі, осы токтар мен кернеулер анықталуға тиіс.
Тармақталған тізбектер тармақтарындағы тоқтарды немесе кернеулерді есептеуді келесі реттілікпен жүргізген ыңғайлы болады:
-коммутациядан кейінгі токтың немесе кернеудің қалыптасқан құраушысын анықтаймыз (іқ uқ)
- коммутациядан кейінгі режим үшін кірістік кедергінің Z(p) (ЭҚК көзі бар тізбектер үшін) немесе кірістік өткізгіштіктің Y(p) (тоқ көзі бар тізбектер үшін) теңдеуін құрып, оны нөлге теңестіреміз. Бұл кезде реактивті кедергілер операторлы түрде келтірілу керек (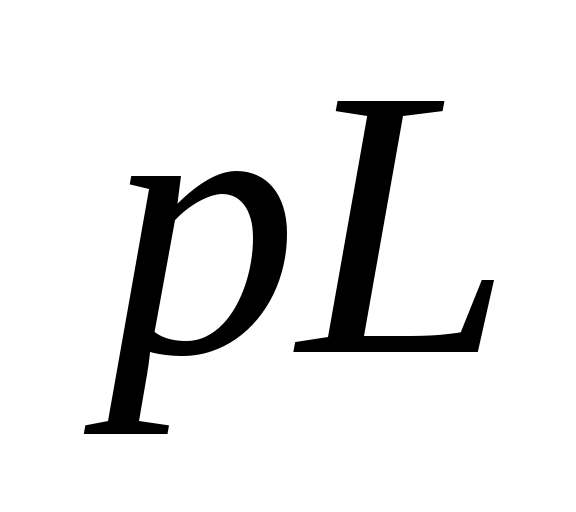 немесе
немесе 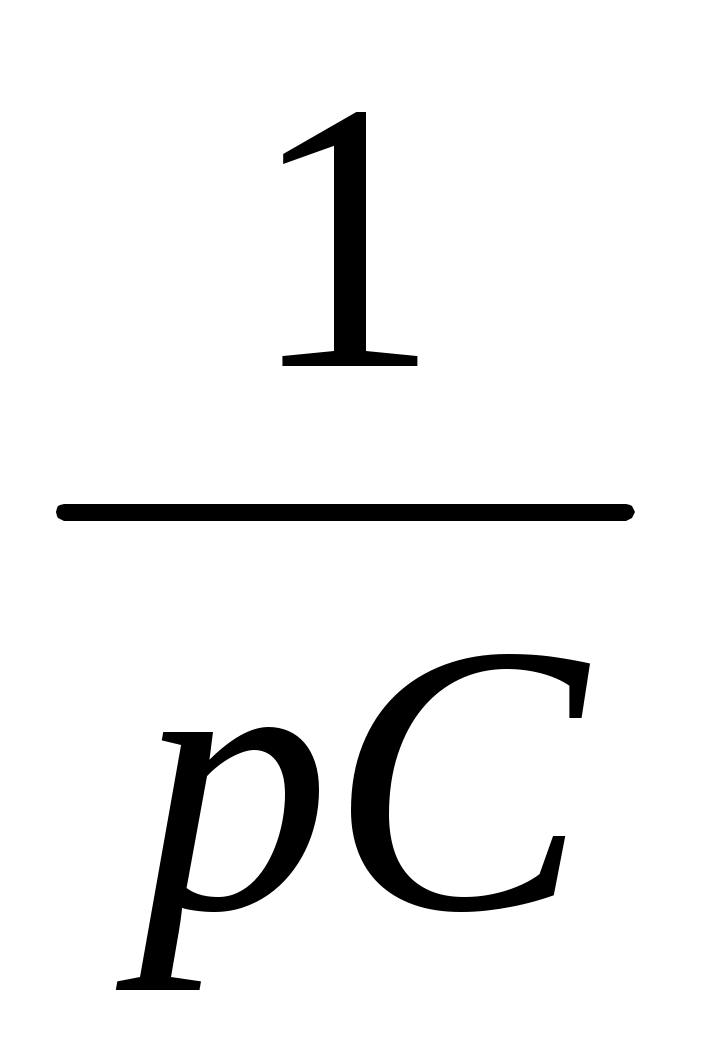 );
);
- түрлендіруден кейін сипаттамалық теңдеуге келеміз, оған берілген параметрлердің мәндерін қойып, өтпелі шаманың еркін құраушысының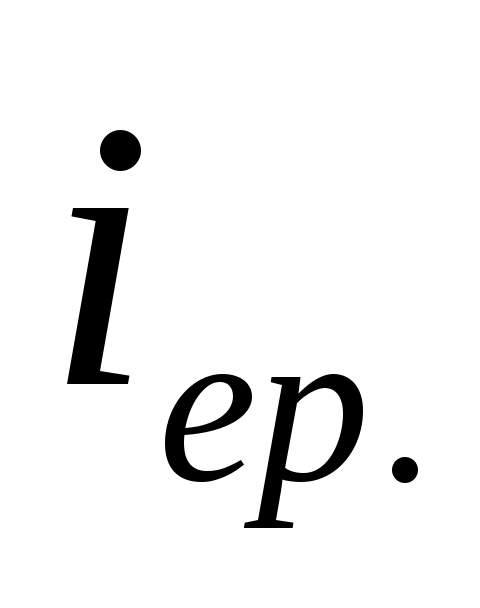 (
(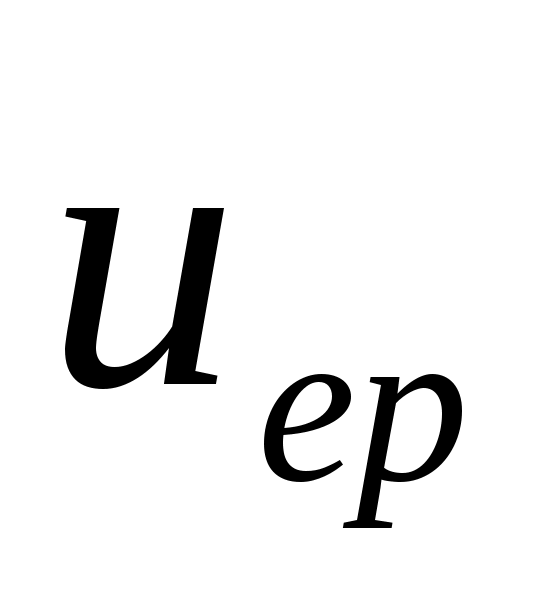 ) түрін анықтайтын теңдеу түбірлерін
) түрін анықтайтын теңдеу түбірлерін  мен
мен  есептейміз. Теңдеу түбірлері теріс таңбалы
есептейміз. Теңдеу түбірлері теріс таңбалы 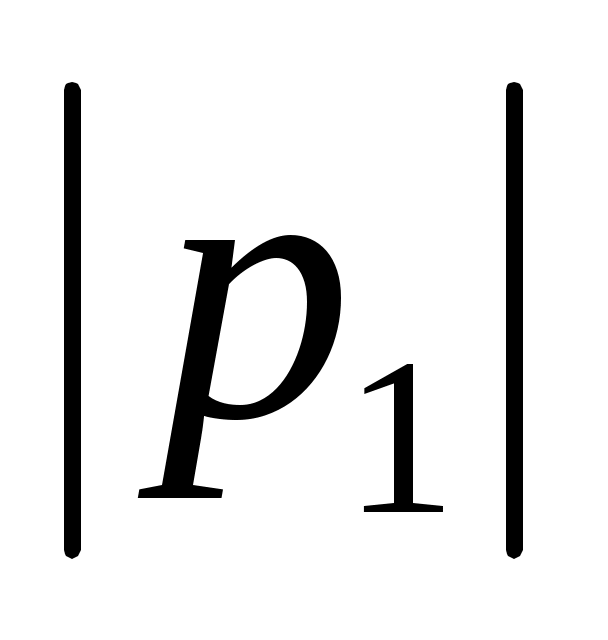 <
<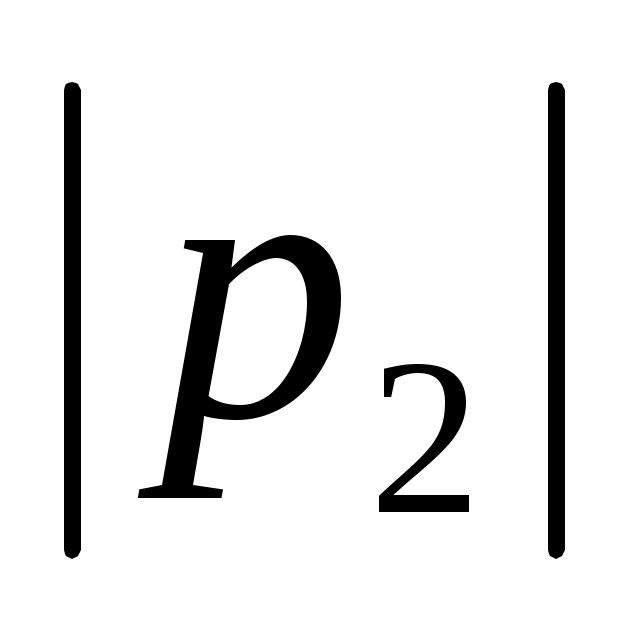
екі нақты сан шықса, онда еркін құраушыларды жазу үшін (13.4) теңдеуін пайдаланамыз, егер =
=  болса - (13.6) өрнегін пайдаланамыз, егер түбірлер кешенді сыбайлас шамалар (
болса - (13.6) өрнегін пайдаланамыз, егер түбірлер кешенді сыбайлас шамалар (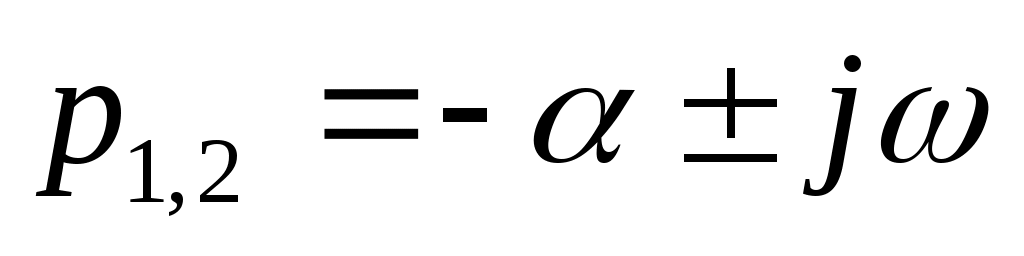 ) болып шықса,
) болып шықса,
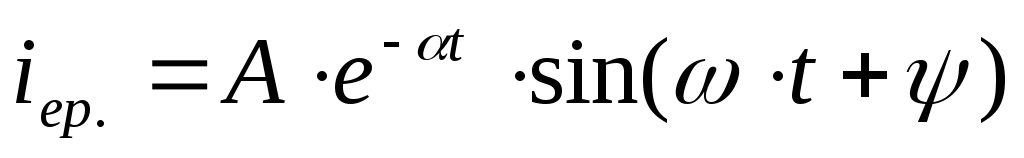 , (5.1)
, (5.1)
мұндағы және
және 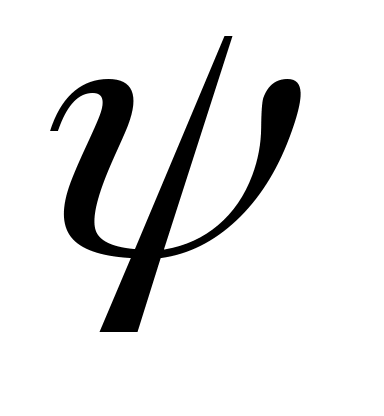 - интегралдау тұрақтылары;
- интегралдау тұрақтылары;
- тоқтың (кернеудің) теңдеуін жалпы түрде жазамыз:
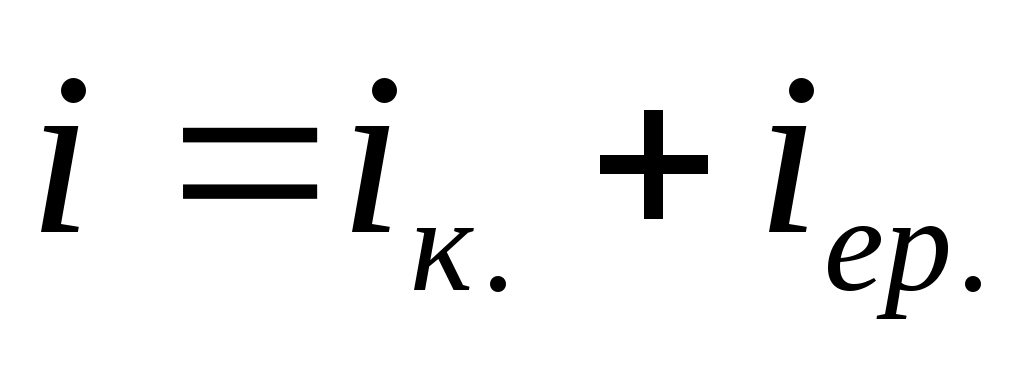 =
= 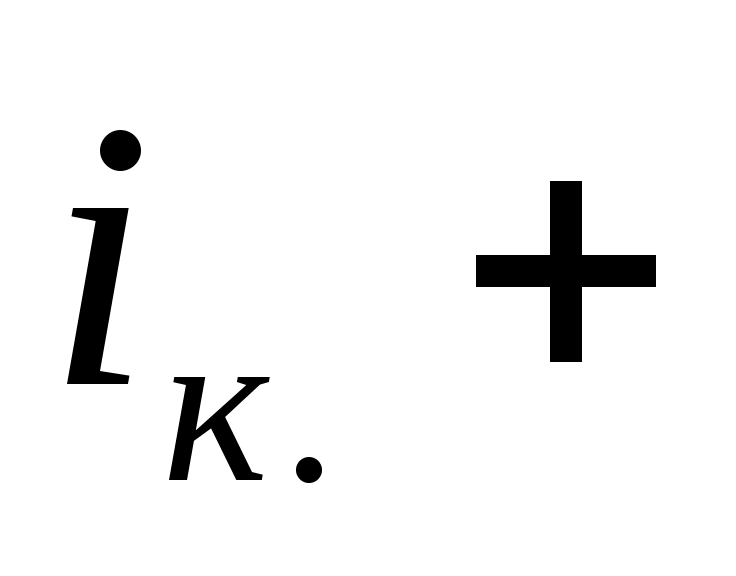
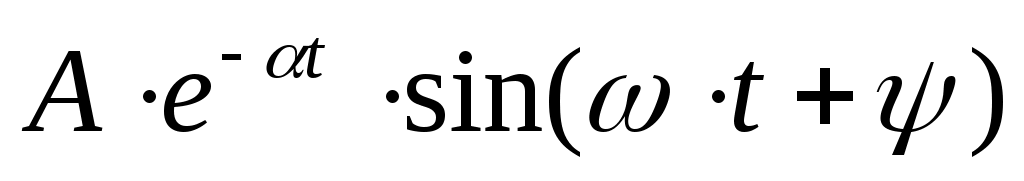 ; (5.2)
; (5.2)
- және
және 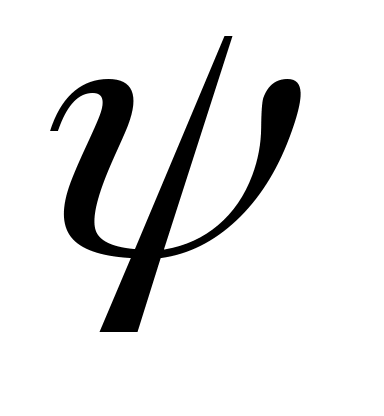 шамаларын есептеу үшін, тағы бір теңдеу қажет, ол үшін тоқтың (кернеудің) уақыт
шамаларын есептеу үшін, тағы бір теңдеу қажет, ол үшін тоқтың (кернеудің) уақыт 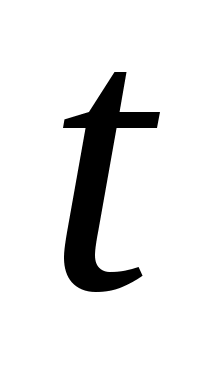 бойынша бірінші туындысын аламыз. Сонда тұрақты ток тізбегі үшін:
бойынша бірінші туындысын аламыз. Сонда тұрақты ток тізбегі үшін:
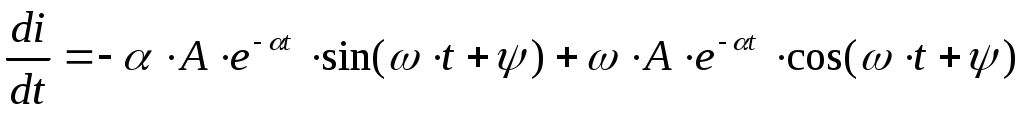 ; (5.3)
; (5.3)
- тоқ (кернеу) және оның туындысының теңдеулерін кезі үшін жазамыз
кезі үшін жазамыз
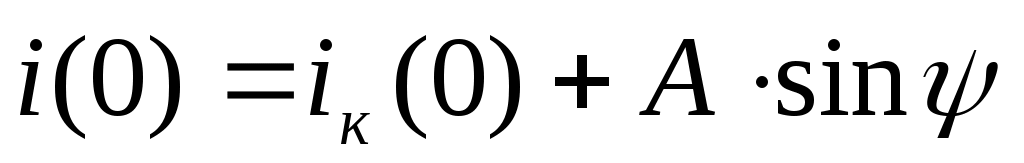 ,
,
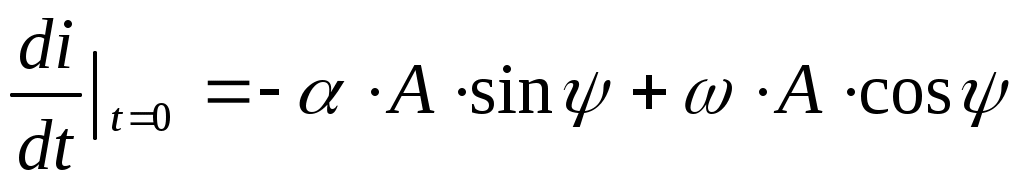 ; (5.4)
; (5.4)
- коммутация заңдары және Кирхгоф теңдеулері бойынша, кезіндегі коммутациядан кейінгі тізбек үшін бастапқы шарттарды анықтаймыз
кезіндегі коммутациядан кейінгі тізбек үшін бастапқы шарттарды анықтаймыз 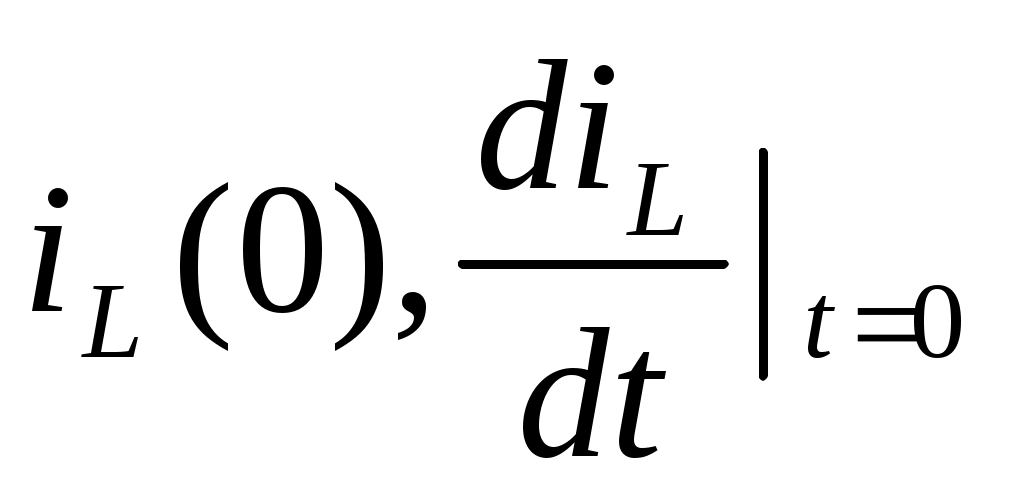 ,
, 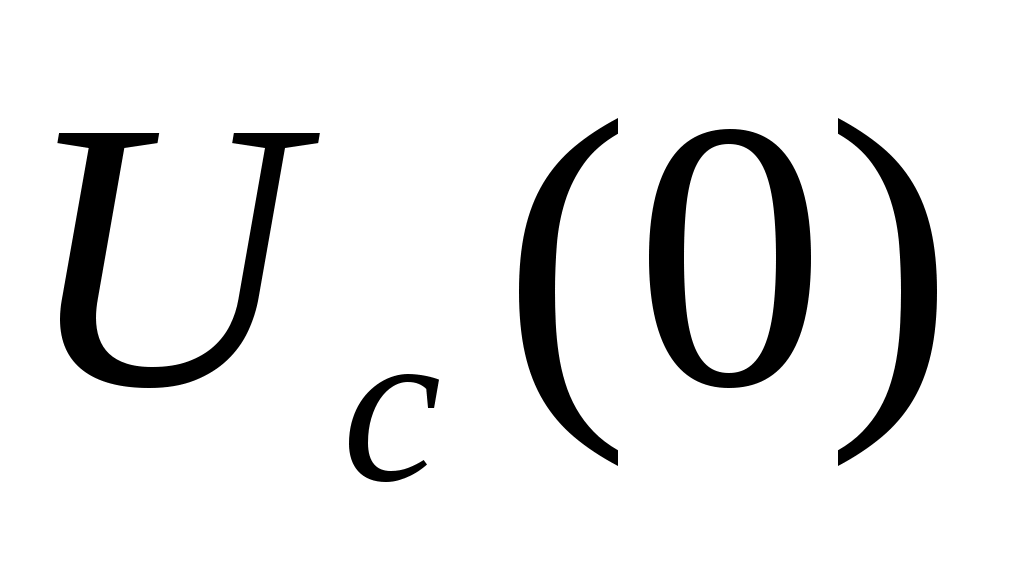 , содан кейін (5.4) өрнектегі
, содан кейін (5.4) өрнектегі  және
және 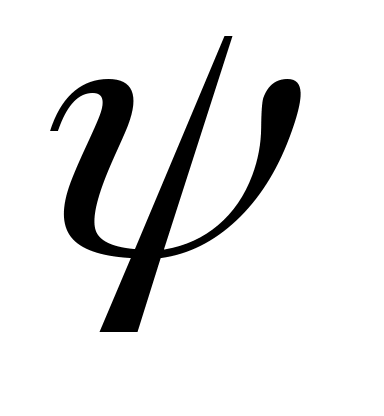
интегралдау тұрақтыларын анықтаймыз;
- және
және  мәндерін өрнегіне қойып, белгілі бір тармақтағы тоқтың
мәндерін өрнегіне қойып, белгілі бір тармақтағы тоқтың 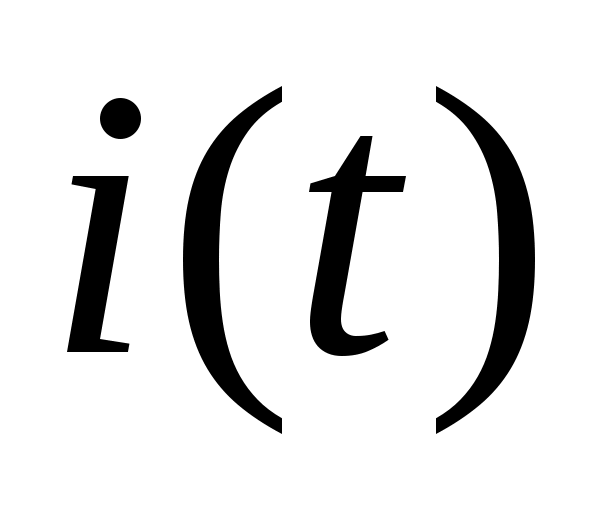 немесе кернеудің
немесе кернеудің 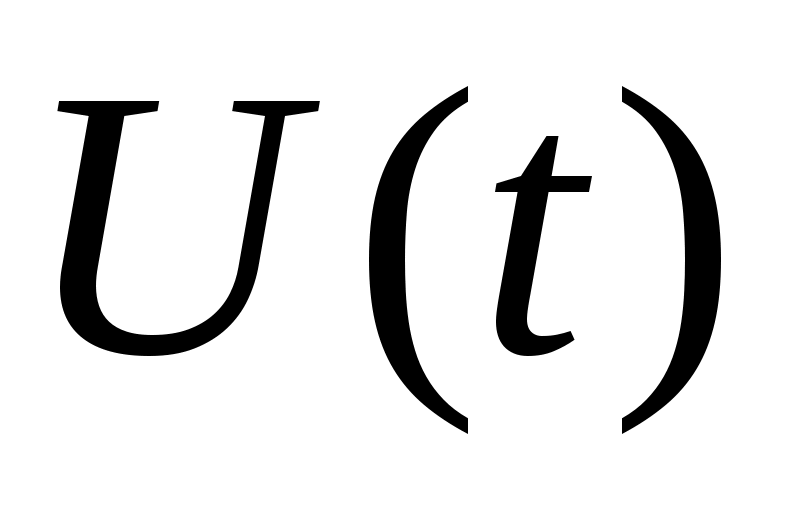 уақыт бойынша өзгеріс заңдылығын анықтаймыз.
уақыт бойынша өзгеріс заңдылығын анықтаймыз.
5.1 Конденсатордың апериодтық разряды. Конденсатордың апериодтық разрядының шектік жағдайы.
Кілтті бір түрге ауыстырғанда конденсатордың зарядталу кезеңі басталады.
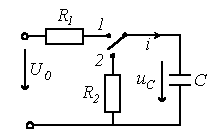
6.1 Сурет
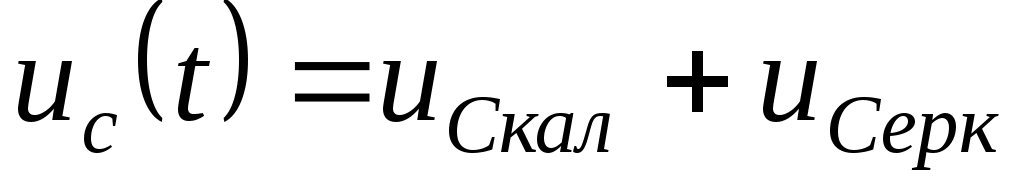 .
.
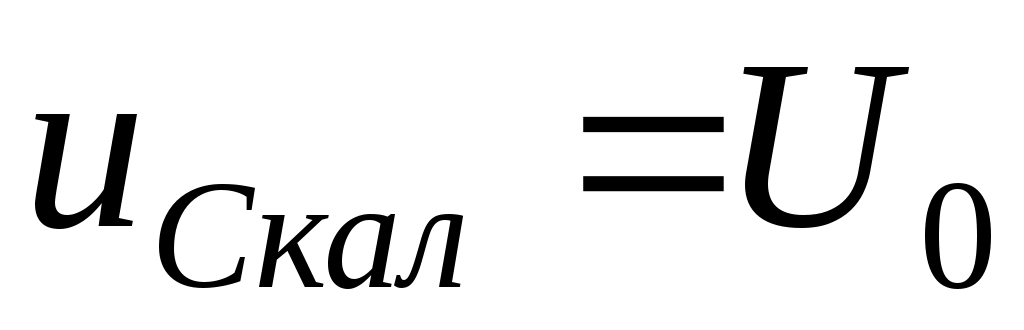 конденсатордағы еріксіз (қалыптасқан) құраушы кернеу.
конденсатордағы еріксіз (қалыптасқан) құраушы кернеу.
Сипаттамалық теңдеуден
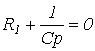
- түбірін анықтаймыз. Осы жерден уақыт тұрақтысы.
Осыдан,
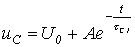 . (5.1)
. (5.1)
t=0 болғанда конденсатор кернеуі - ға тең (жалпы жағдайда коммутация кезінде конденсатор зарядталған болуы мүмкін). Сондықтан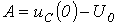 және
және
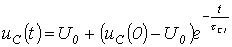 . (5.2)
. (5.2)
Зарядталған тоққа қатысты былай жазуға болады.
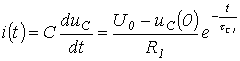 . (5.3)
. (5.3)
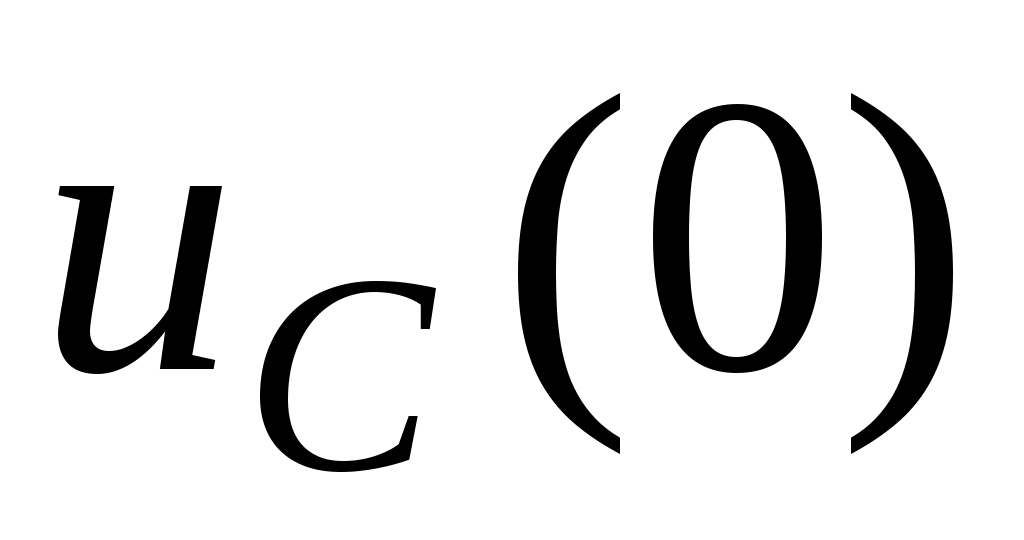 шамасына байланысты:
шамасына байланысты:
1. -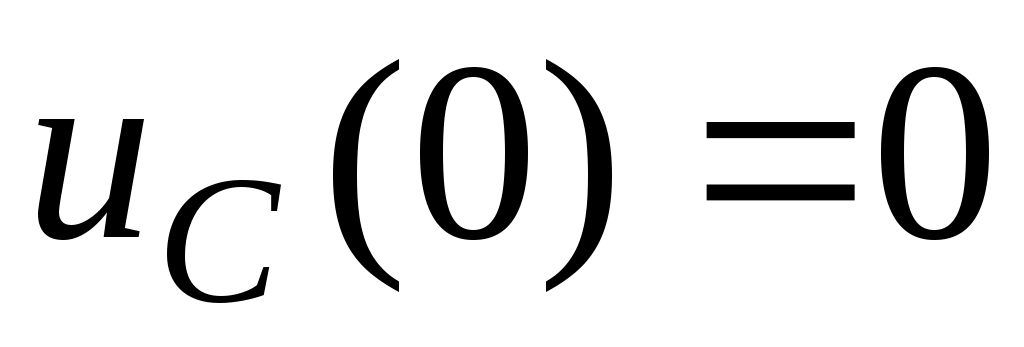 ;
;
2. -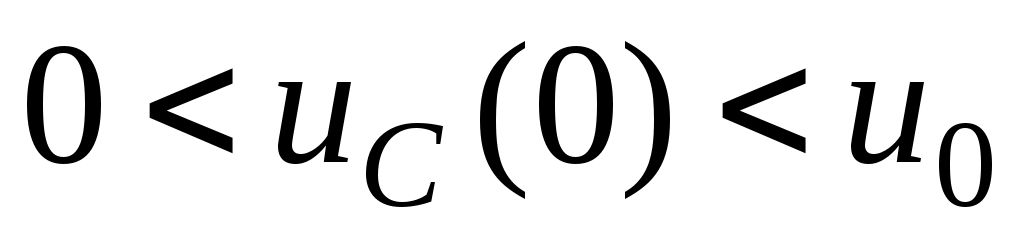 ;
;
3. -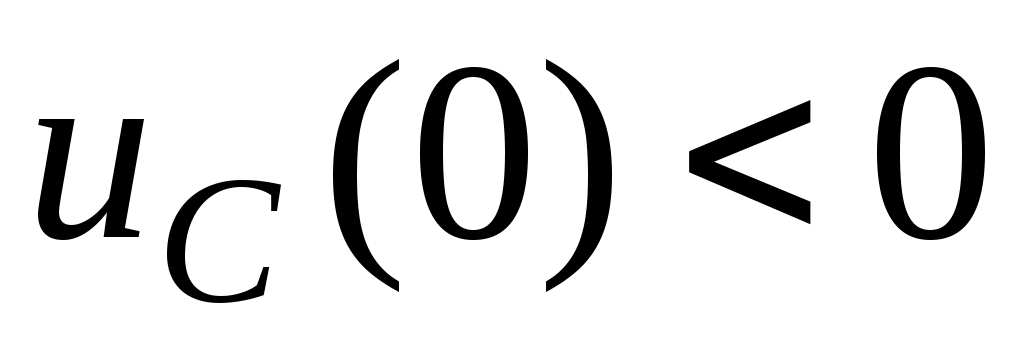 ;
;
-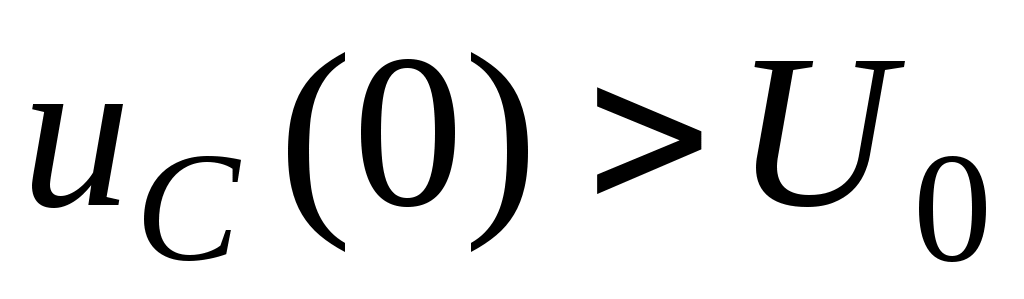 - осыдан төрт қисық өтпелі кезең болуы мүмкін, 6.2 суретте көрсетілген.
- осыдан төрт қисық өтпелі кезең болуы мүмкін, 6.2 суретте көрсетілген.
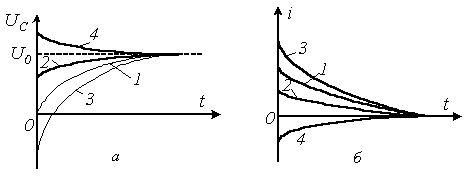
5.2 Сурет
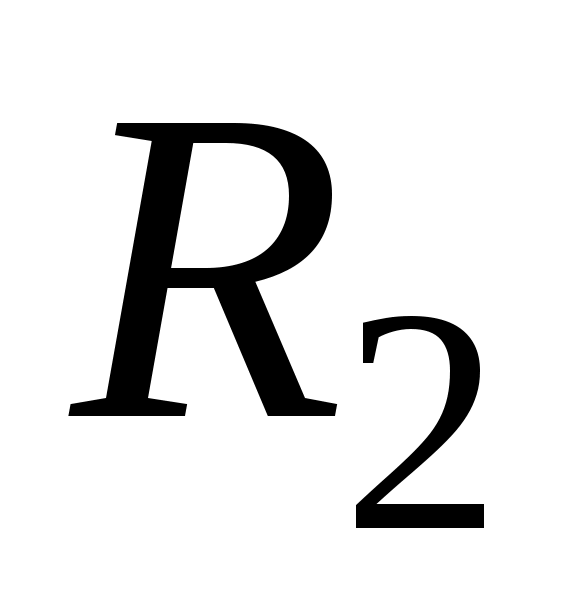 резисторында конденсатор разрядталса (5.1 суретіндегі кілт 2 түрге ауыстырылады)
резисторында конденсатор разрядталса (5.1 суретіндегі кілт 2 түрге ауыстырылады) 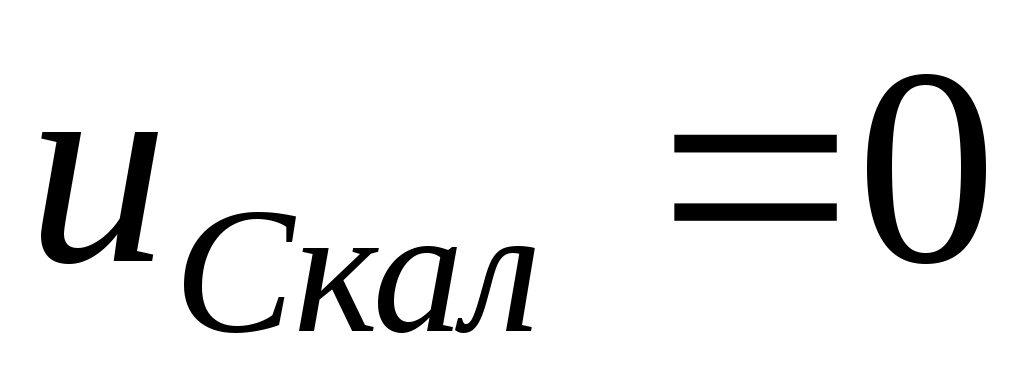 . Уақыт тұрақтысы
. Уақыт тұрақтысы 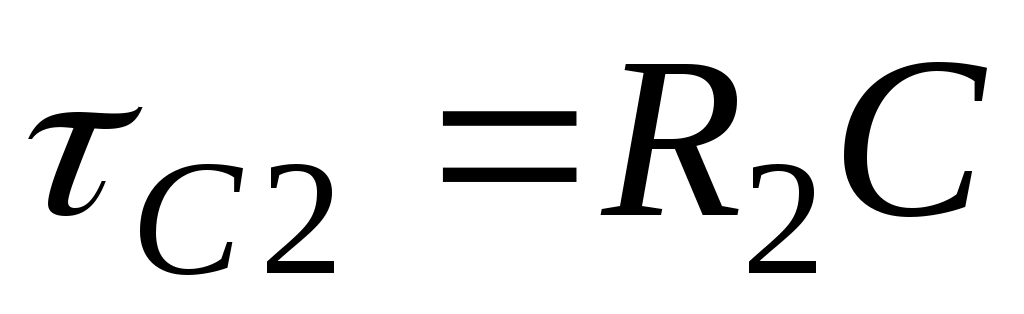 .
.
Коммутация кезінде конденсатор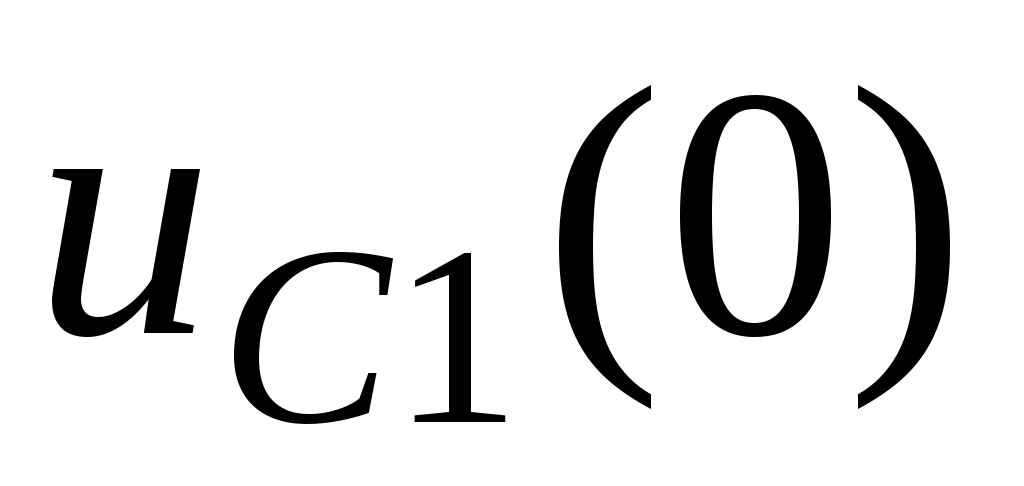
Абсолюттік шамасы бойынша |
б)
Бұл режим критикалық деп аталады.
в)
мұндағы
Бұндай режим периодтық немесе тербелмелі деп аталады. Бұл жерде орауыш пен конденсатор арасында көп мөлшердегі энергия алмасуы жүріп өтеді: энергия бірде магниттік өріске (тоқ өскен кезде), бірде электр өрісіне (конденсатордағы кернеу өскенде) ауысып құйылатындай болады.
Интегралдау тұрақтылары бастапқы шарттардан анықталады.
, (4.9)
(4.10) теңдеулерінен
№5 дәріс 5. Классикалық әдіспен өтпелі кезеңдерді есептеудің жалпы жағдайы.
Дәрістің мақсаты: тармақталған тізбектердегі өтпелі кезеңдерді классикалық әдіспен және тізбектің кез келген кернеу көзіне қосылуы кезіндегі есептеулерді меңгеру.
Берілген есеп, тоқтар мен кернеулердің лездік мәндері үшін Кирхгоф заңдары бойынша құрастырылған теңдеулер көмегімен шешіледі, осы токтар мен кернеулер анықталуға тиіс.
Тармақталған тізбектер тармақтарындағы тоқтарды немесе кернеулерді есептеуді келесі реттілікпен жүргізген ыңғайлы болады:
-коммутациядан кейінгі токтың немесе кернеудің қалыптасқан құраушысын анықтаймыз (іқ uқ)
- коммутациядан кейінгі режим үшін кірістік кедергінің Z(p) (ЭҚК көзі бар тізбектер үшін) немесе кірістік өткізгіштіктің Y(p) (тоқ көзі бар тізбектер үшін) теңдеуін құрып, оны нөлге теңестіреміз. Бұл кезде реактивті кедергілер операторлы түрде келтірілу керек (
- түрлендіруден кейін сипаттамалық теңдеуге келеміз, оған берілген параметрлердің мәндерін қойып, өтпелі шаманың еркін құраушысының
екі нақты сан шықса, онда еркін құраушыларды жазу үшін (13.4) теңдеуін пайдаланамыз, егер
мұндағы
- тоқтың (кернеудің) теңдеуін жалпы түрде жазамыз:
-
- тоқ (кернеу) және оның туындысының теңдеулерін
- коммутация заңдары және Кирхгоф теңдеулері бойынша,
интегралдау тұрақтыларын анықтаймыз;
-
5.1 Конденсатордың апериодтық разряды. Конденсатордың апериодтық разрядының шектік жағдайы.
Кілтті бір түрге ауыстырғанда конденсатордың зарядталу кезеңі басталады.

6.1 Сурет
Сипаттамалық теңдеуден
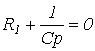
- түбірін анықтаймыз. Осы жерден уақыт тұрақтысы.
Осыдан,
t=0 болғанда конденсатор кернеуі - ға тең (жалпы жағдайда коммутация кезінде конденсатор зарядталған болуы мүмкін). Сондықтан
Зарядталған тоққа қатысты былай жазуға болады.
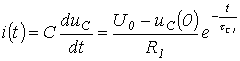 . (5.3)
. (5.3)1. -
2. -
3. -
-

5.2 Сурет
Коммутация кезінде конденсатор