Егер де солжақтағы жартылай жазықтықта орналасқан Z(p) функцияның нөлдері нақтылы білікте жатса, онда апериодикалық процесс болады; нөлдер бір нүктеде болса аумалы жағдай, егерде Z(p) функциясының нөлдері комплексті ілестіру болса, онда тербелу процесс болады.

болғанда оралып өтетін қисықтың ординатасы 2,72 есе басты мәнінен аз болады. Сондықтан шаманы тербелу контурдың уақыт тұрақтысы деп атайды.





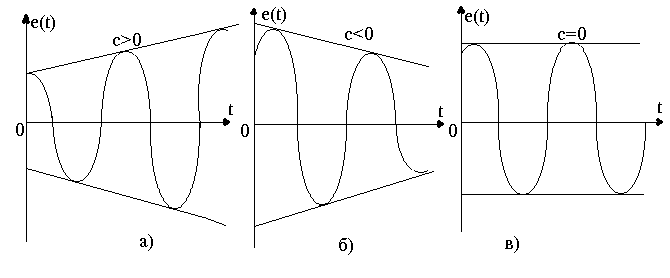
6.5-сурет. Өсетін (а), азаятын (б) және (в) амплитудалары бар синусоидалар

№7 дәріс 7. Өтпелі кезендерді операторлық есептеу жалпы жағдайы.

---

7.1 Лапластың түрлендіруін өтпелі прцестерді есептеуге қолдану

Өтпелі процестерді классикалық әдіспен есептеу басты жағдай бойынша интегралдаудың тұрақтылардың белгілеу және басты функцияларды және олардың туындыларын табу үшін алгебралық теңдеулердің жүйесін дүркін-дүркін шешуді талап етеді. Бұл жағдай осы әдіспен есептеудің негізгі қиыншылығына жатады. Электр схемалар күрделенген сайын және дифференциялды теңдеудің дәрежесі өскен сайын бұл қиыншылықтар өседі.

Сондықтан, тапсырылған басты жағдайлар бастапқы теңдеулерге кіргізіліп сызықты дифференциалды теңдеулерді шешу әдісті пайдалану қолайлы болады, өйткені бұл әдісте керекті функцияларды табу үшін интегралдаудың тұрақтыларын белгілеудің қажеттігі жоқ болады.

Сызықты дифференциалды теңдеулерді Лапластың түрлендірулерге негізделген операторлық әдіспен интегралдауға болады.

Операторлық әдістің маңызы – түп нұсқа деп аталатын кейбір тапсырылған бір қатарлы шектелген заттық айнымалының f(t) функциясына басқа кескін деп аталатын комплексті айнымалының F(p) функция салыстырылады. Функция f(t) әрбір ақырғы уақыт аралықта Дирихле жағдайына қамтамасыз ету керек және t0 кезде нөлге тең болу керек.

Салыстыру мына формула бойынша өткізіледі

(7.1)

(7.1) формула - f(t) функцияның үстінен Лапластың тікелей түрлендірудін көрсетеді.

Оны былай белгілейді:

немесе F(p) f(t),

мұнда F(p) - f(t) функциянын Лапластық кескіні:

Егерде, кері F(p) кескіні бойынша түп нұсқаны табу керек болса, онда Лапластың кері түрлендіруі қолданады

(7.2)

яғни (10.1) интегралды теңдеудің f(t) функцияға қатысты шешу. (7.2) интегралды былай белгілеуге де болады

немесе

---

Түр нұсқаудан туындылардың және интегралдаудың кескіндері үшін формулаларын (шығарусыз) келтірейік:

Егер де болса, онда (7.3)

(7.4)

және т. с. с. (7.5)

Егер де f(t) функция және оның туындылары f^I(t), f^II(t),… t=0 кезде кенет өзгерсе, онда (10.4) және (10.5) формулаларға олардың мәнін осы кенет өзгерісті есепке алып қою керек, яғни нөлдің оң жағында, бұл жағдай олардың аргументтерінде 0+ белгімен көрсетілген. Егер де t=0+ кезде функцияның және оның туындыларының басты мәндері нөлге тең болса, онда бірінші және одан соңғы туындылардың кескіндері өте жеңіл табылады:

(7.6)

Түп нұсқаудан интегралдаудың кескіндерінің түрі:

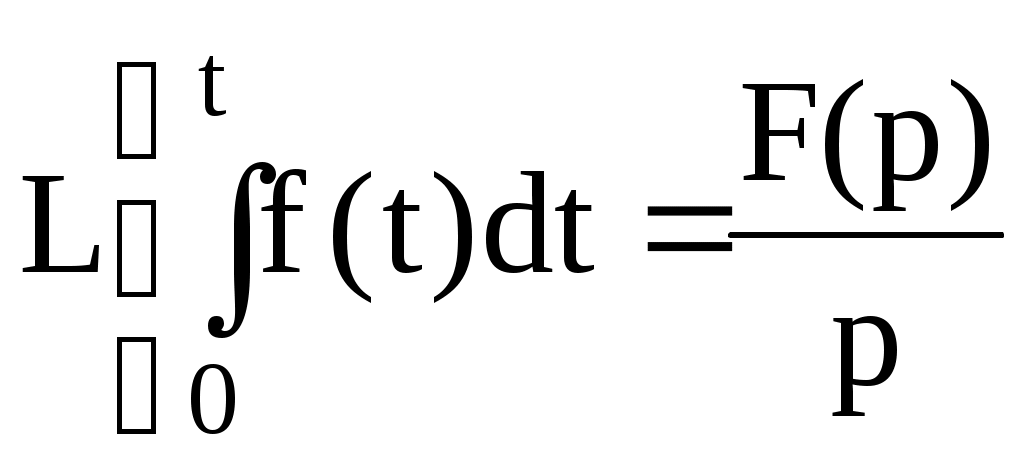(7.7)

(7.8)

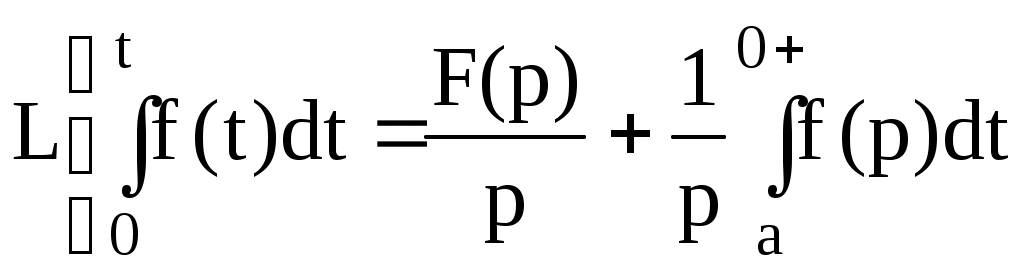
Егер де интеграл t=0 кезде кенет өзгерсе, онда оның мәнін нөлдің оң жағынан алу керек, бұл жағдай оның жоғарғы шегіне 0+ белгімен көрсетілген.


7.2 Жіктеудің теоремасы

Кескін дұрыс бөлшек түрде берілсін, алымның және бөлгіштің жалпы түбірлері жоқ. F(p) функциясын полюстерінің орыны F₂(p)=0 (7.8) теңдеудің түбірлерімен белгіленеді.

(7.8) теңдеудің n түбірлерін р₁, р₂,…р_n деп белгілейміз.

Екі жағдай болуы мүмкін: а) барлық түбірлер жай;

б) кейбір немесе барлық түбірлері еселі

а) Жай түбірлердің жағдайы

Өте жай жағдайда кескін рациональды бөлшек түрде болады

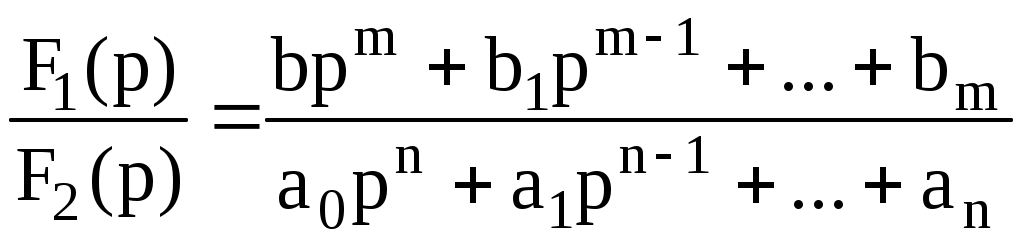m
F₁(p)/F₂(p) бөлшек қысқарылмайды, яғни F₁(p) және F₂(p) көп мүшелердің жалпы түбірлері жоқ, ал а_к және в_к-заттық сандар. (9.8) кескіннің түп нұсқасын жіктеу теоремасы деп аталатын формула бойынша табуға болады

---

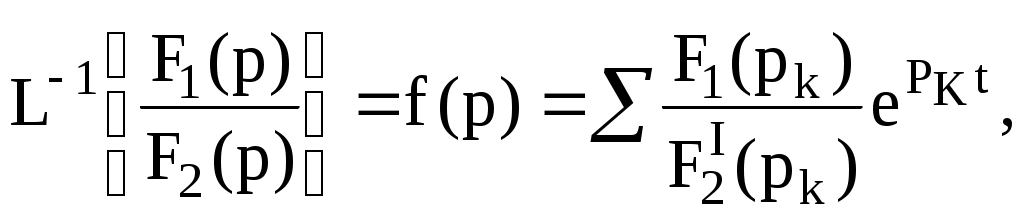
(7.9)

мұнда р_К сипаттамалы теңдеудің F₂(p)=0 жай түбірлері, бір түбір нөлге тең болуы мүмкін.

Егер де бір түбір нөлге тең болса, яғни бөлгіш ішінде (7.9) р көбейткіш бар болса, онда жіктеу теореманың басқа түрі қолданады.

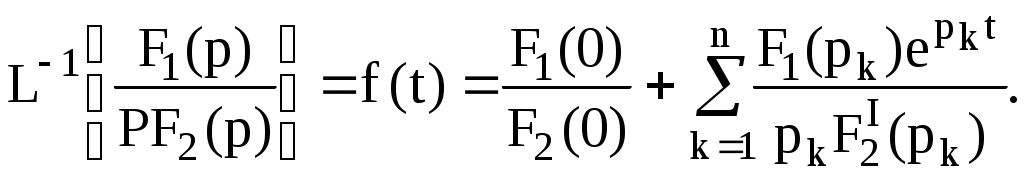(7.10)

б) Еселі түбірлердің жағдайы

Егер де көп мүшелі F₂(p) түбірлерінің ішінде еселі түбірлер болса, онда жіктеу теореманы (7.11) және (7.12) формулаға ұқсасты жазуға болады, бірақ оң жағында қос қосындымен (бір қосынды түбірлер саны бойынша, ал екінші-әрбір түбір үшін оның еселік реттігімен).

Сонымен, F₂(p)=0 теңдеуде еселі түбірлер болса, онда кескіні бойынша түп нұсқау мына формула бойынша есептеледі:

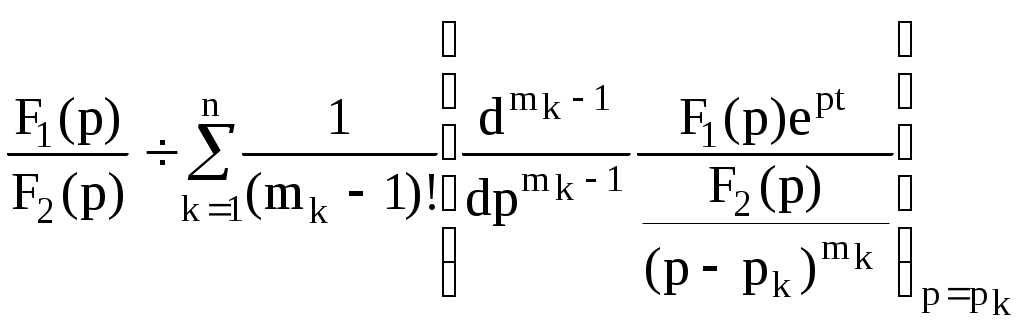(7.11)

Квадрат жақшаның бөлгішіндегі көріністі алдымен (p-p_k)^m_k шамаға қысқартып, содан кейін дифференциялдау керек.

Егер де F₂(p)=0 теңдеуде бір мезгілде жай және еселі түбірлер болса, онда жай түбірлерге сәйкесті қосындыларды (7.9) және (7.10) формулалар, ал еселі түбірлер үшін (7.11) формула қолданады.


№8 дәріс 8. Операторлық формадағы Ом және Кирхгоф заңдары.
8.1-суреттегі r, L, C тізбек e₁(t) ЭҚК-ке қосылып тұрған, ал t=0 уақыт мезгілде e(t) ЭҚК-ке ауысып қосылады.

Ауысып қосылып кейін Ом заңы лезді мәндер үшін былай жазылады


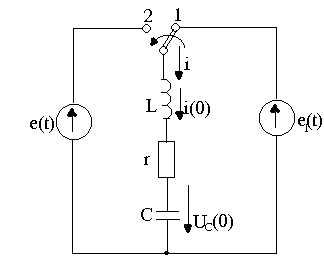
(8.1)

8.1-сурет

(8.2)

мұнда U_C(0)-сыйымдылықта ауысып қосу кездегі кернеу, яғни t=0 кезде.

Лезді мәндер үшін жазылған Ом заңынан оның операторлық түрде жазылған көрінісіне өту үшін (9.1) формулаға сәйкес былай істеледі: (8.1) теңдіктің екі жағын шамаға көбейтіп нөлден шексіздікке дейін интегралдау керек. Сонда шығады

---

деп есептеп шығарамыз



ал бұл теңдеуден r, L, C тізбек үшін операторлық түрде Ом заңы шығады

. (8.3)
Бөлгіште тұрған көрініс операторлық кедергі деп аталады.

. (8.4)

Операторлық кедергіге кері шама операторлық өткізгіш деп аталады . (8.5)

Басты жағдайлар нөлге тең болса, яғни i_L(0)=0 және U_C(0)=0 болса, онда (9.16) көрініс

(8.6)

яғни комплексті түрдегі Ом заңына толық ұқсас. Тармақталған тізбектің әрбір түйіні үшін сондықтан токтың кесіндісін белгілеп Кирхгофтың бірінші заңын операторлық түрде жазамыз

(8.7)

n тармақтан құралған әрбір тұйықталған контур үшін



деп есептеп Киргофтың екінші заңы операторлық түрде жазылады

ал мұны былай жазуға болады

(8.8)

Бұлай жазылған түрде және -индуктивтік орауыштардағы токтың және конденсаторларды кернеудің басты мәндері.

Егер де басты жағдайлар нөлге тең болса, онда Киргофтың екінші заңы былай жазылады

(8.9)

яғни бұл жағдайда ол Киргофтың екінші заңы комплексті түрде жазылғанға толық ұқсас.

Сонымен, Ом және Киргофтың заңдары операторлық түрде өздерінің жазылу түрі бойынша синусоидалды ток тізбегі үшін сол заңдардың комплексті түрі жазылғанға ұқсас. Бірақ есте ұстау керек, бірінші-басты жағдайлар нөлге тең болмағанда, яғни

---

Смотрите также файлы

• Виды клизм Механизм действия.docx

• Гироскопический датчик Создание проекта.docx

• 1 общая характеристика объекта исследования.docx

• Тема Обеспечение реализации требований фгос к условиям реализации основных образовательных программ. Практическая работа 2.docx

• Swot анализ ооо Азбука Вкуса.docx