Файл: Дрістер жинаы (15 саат) etn (II) 2216 Электр техниканы теориялы негіздері (II).doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 161
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
кернеуінде зарядталған болса (кейбір кезде 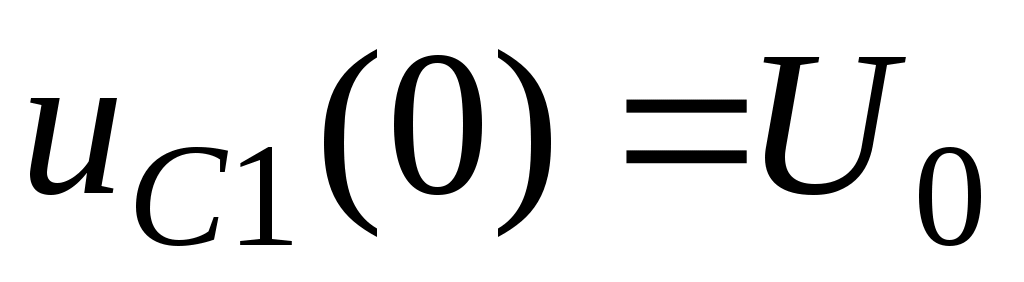 ), өтпелі ережеде кернеуді былай жазуға болады.
), өтпелі ережеде кернеуді былай жазуға болады.
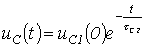 . (5.4)
. (5.4)
Сәйкесінше разрядты тоқ
Өтпелі кезеңде RLC- тізбегін кернеу көзіне тізбектей .
Мына жағдайды қарастырайық
Алдыңғы дәрісте қарастырғандай өтпелі кезеңдегі классикалық әдісті конденсатордағы кернеуді 3.3 суретіндегі тізбекке қарап былай жазуға болады.
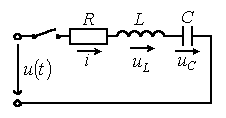
6.3 Сурет
Тізбектің сипаттамалық теңдеуі
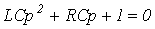 ,
,
Осыны шешіп, келесіні аламыз
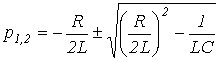 .
.
Тізбек көрсеткіштерінің арақатынасына байланысты үш түбір болуы мүмкін және еркін құрастырушылар үшін үш нұсқа қарастырамыз:
1.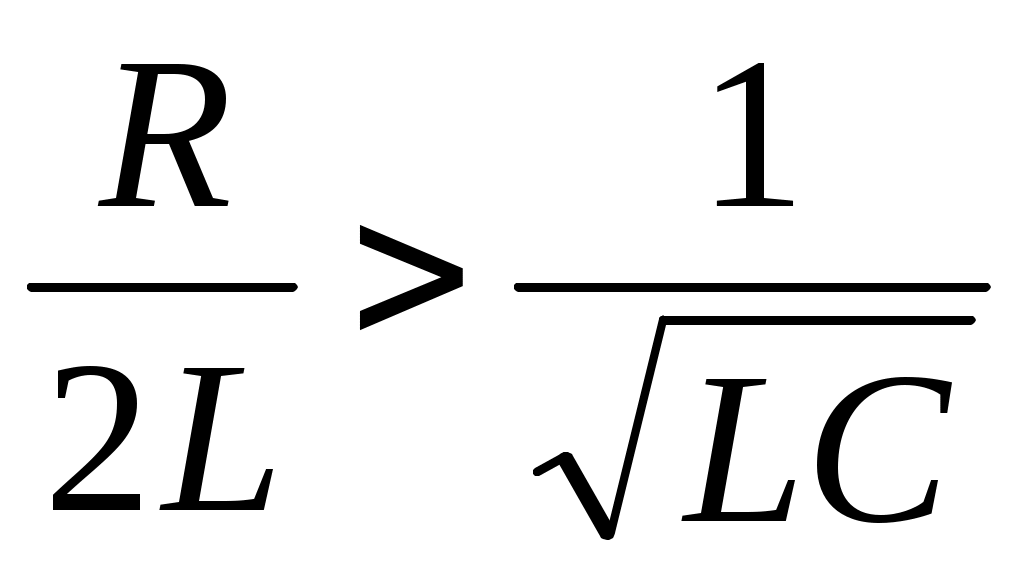 немесе
немесе 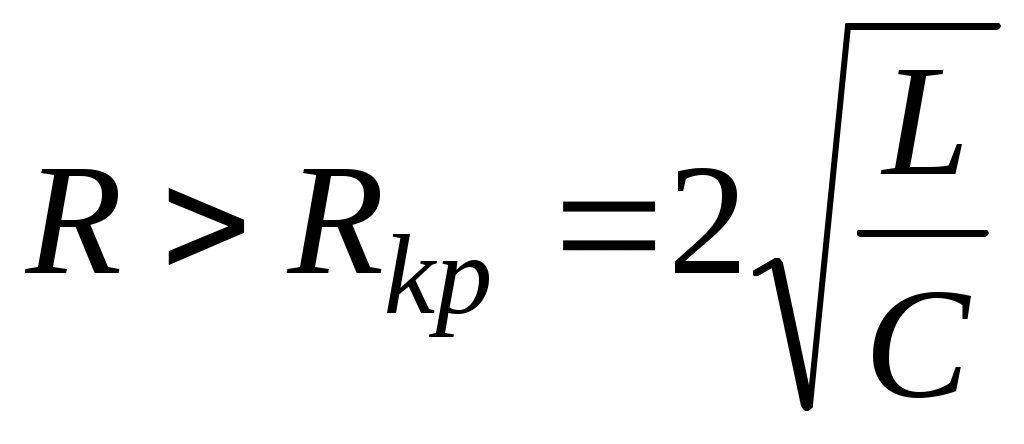 , мұндағы
, мұндағы 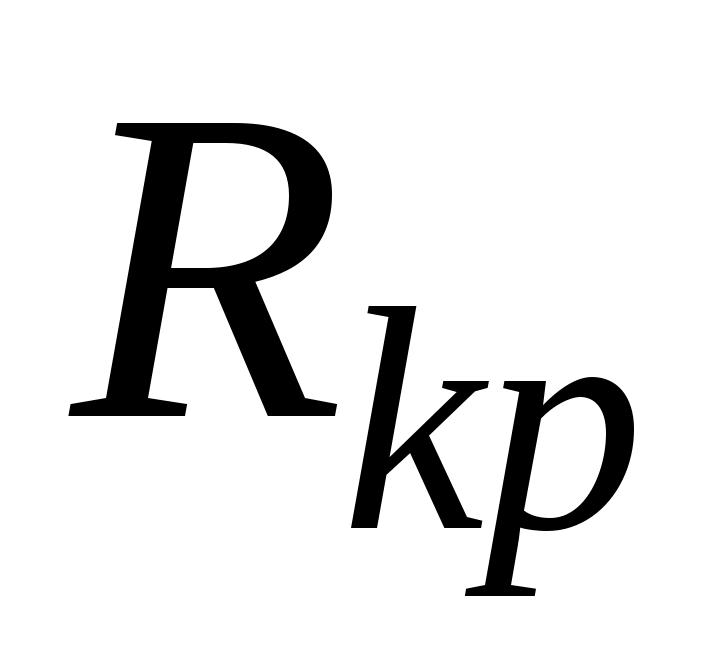 - контурдың критикалық кедергісі, еркін кезең кіші тербелмелі сипаттамасын бірге алып жүреді.
- контурдың критикалық кедергісі, еркін кезең кіші тербелмелі сипаттамасын бірге алып жүреді.
2.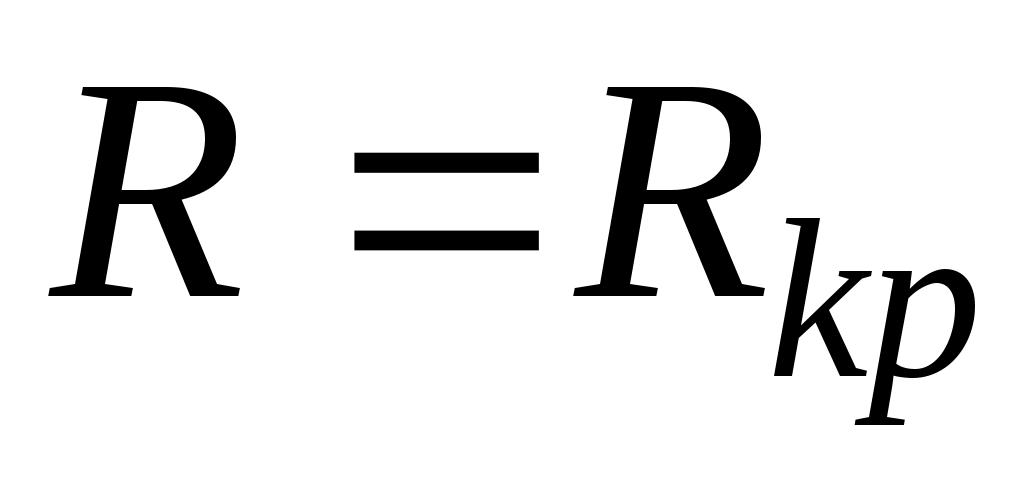 - периодикалық емес ереженің шегі.
- периодикалық емес ереженің шегі.
Осы жағдайда
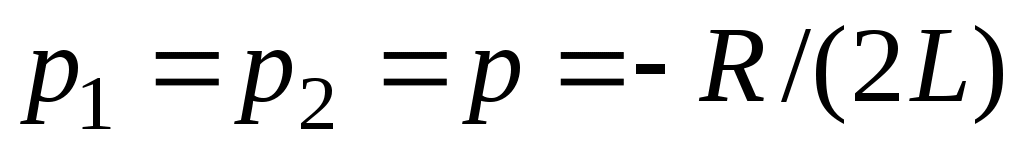 және
және
3.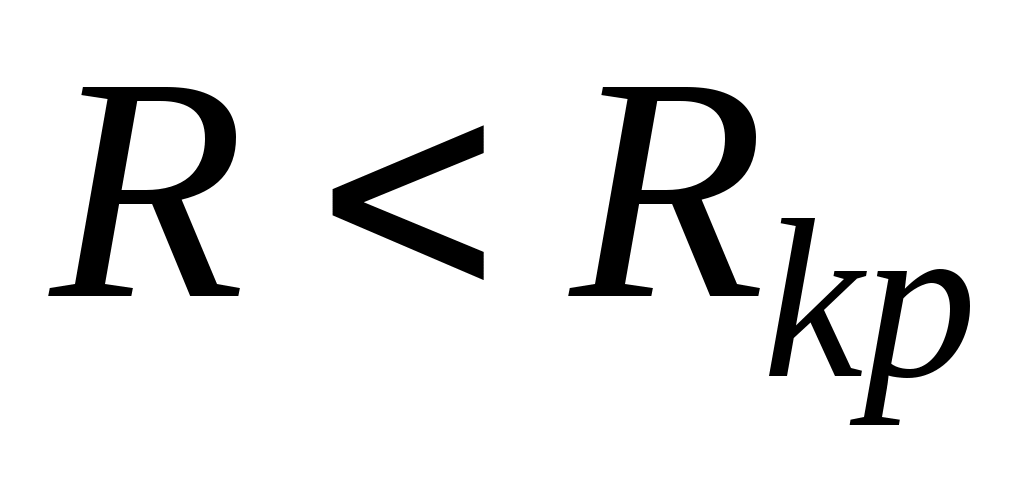 - өтпелі кезеңнің периодикалық (тербелмелі) сипаттамасы.
- өтпелі кезеңнің периодикалық (тербелмелі) сипаттамасы.
Осы жағдайда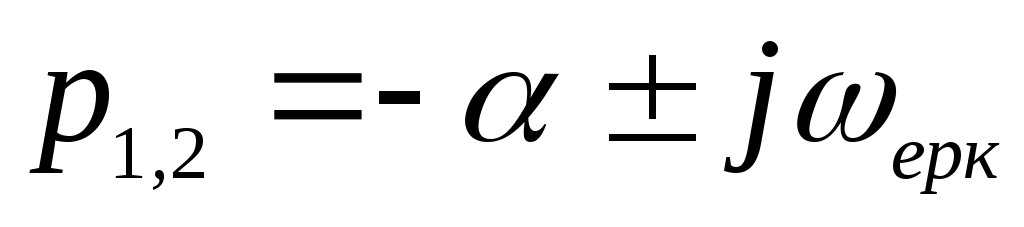 және
және
мұндағы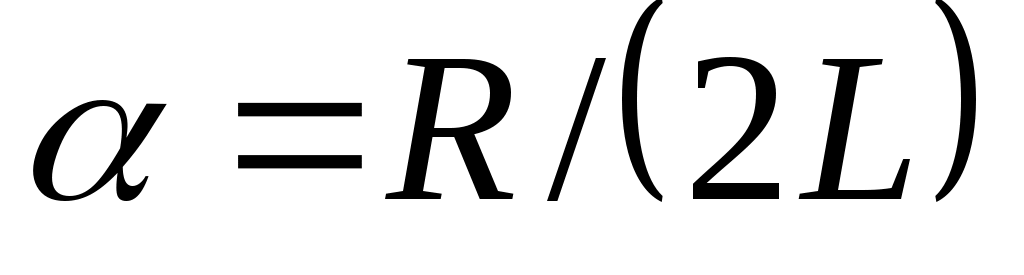 - өшу еселеуіші;
- өшу еселеуіші;
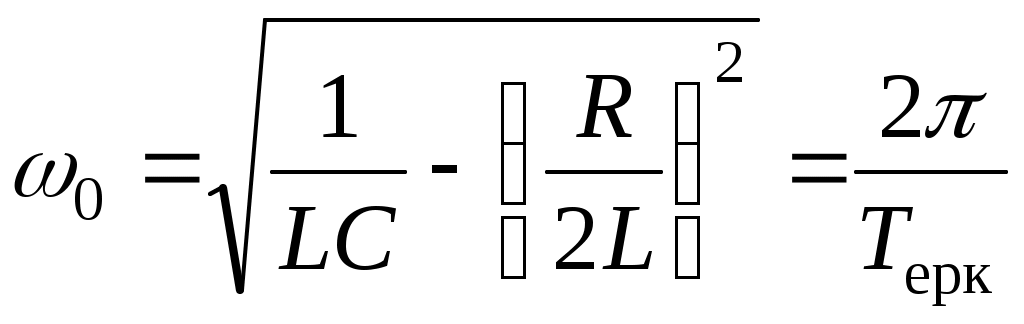 - өзінің немесе еркін тербелістің бұрыштық жиілігі;
- өзінің немесе еркін тербелістің бұрыштық жиілігі;
- өздік тербелістің периоды.
Өтпелі кезеңнің периодикалық емес сипаттамасы үшін мынаны жазуға болады:
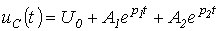 .
.
Интегралдау тұрақтысын табу үшін, жалпы жағдайда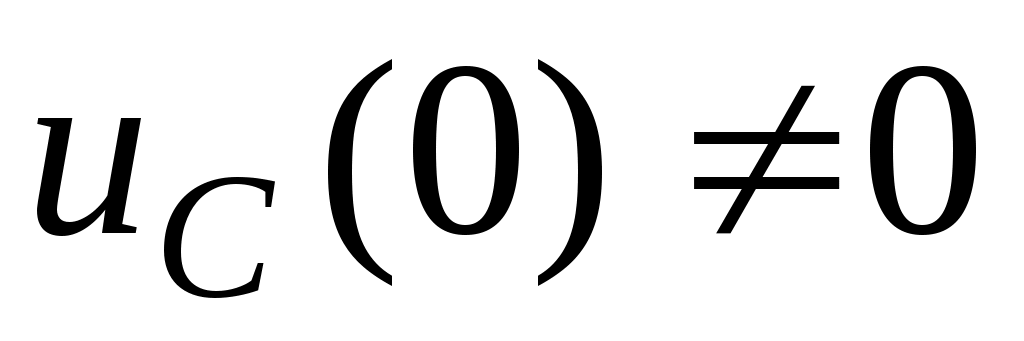 және коммутацияның бірінші заңына қатыстыи в соответствии с первым законом коммутации
және коммутацияның бірінші заңына қатыстыи в соответствии с первым законом коммутации 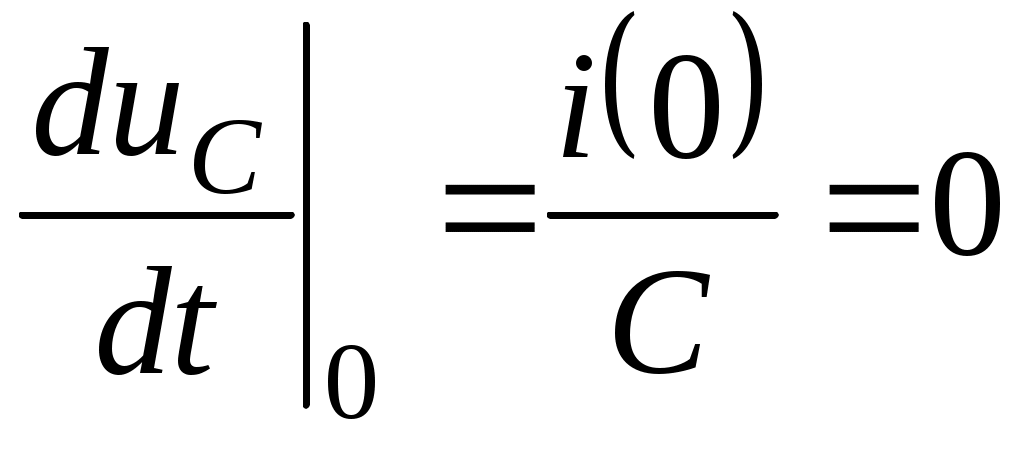 , t=0 үшін екі теңдеу жазамыз.
, t=0 үшін екі теңдеу жазамыз.
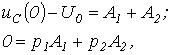
Осыны шешіп, келесіні аламыз
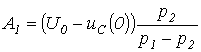 ;
; 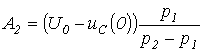 .
.
Сондықтан,
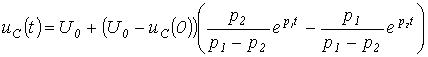 .
.
Сонда тізбектің тоғы
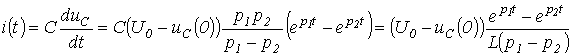
орамадағы индуктивті кернеу
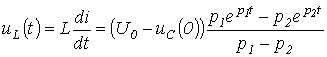 .
.
5.4 суретінде , және сапалы кедергілер берілген, периодикалық емес өтпелі кезеңге қатысты.
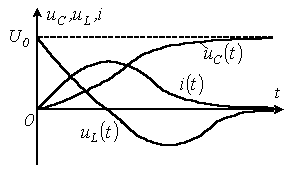
5.4 Сурет
Критикалық ереже үшін былай жазуға болады.
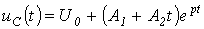 .
.
болағанда
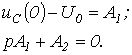
Сондықтан,
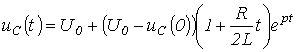
және
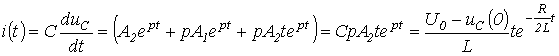 .
.
Тербелмелі өтпелі ереже үшін
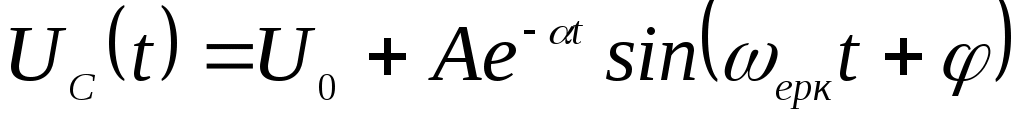 .
.
Интегралдау тұрақтысын табу үшін
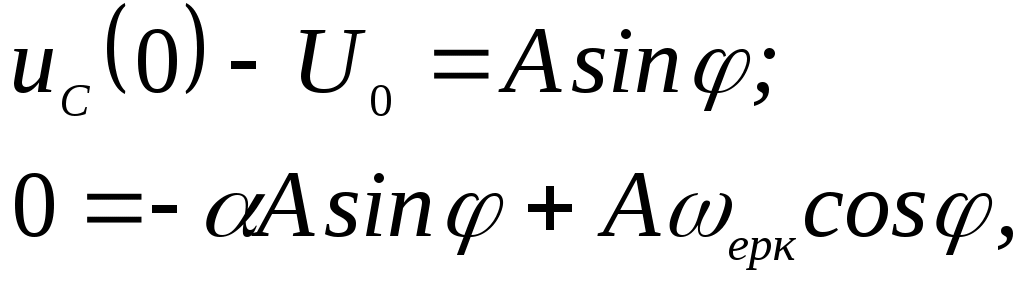
Осыдан
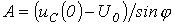 және .
және .
сонда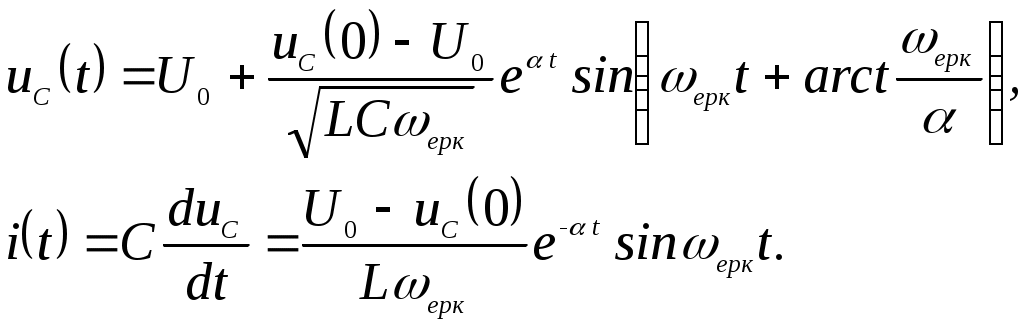
5.5 суретте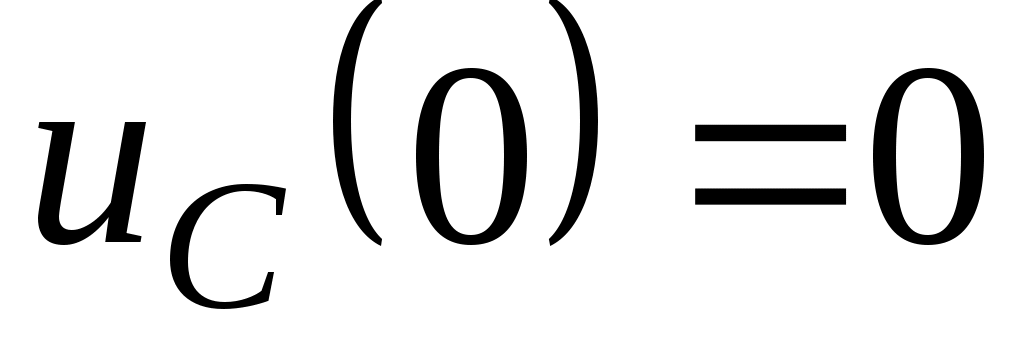 кезінде тербелмелі өту кезеңіне сәйкес сапалы қисықтар Uc(t) және i(t)көрсетілген
кезінде тербелмелі өту кезеңіне сәйкес сапалы қисықтар Uc(t) және i(t)көрсетілген
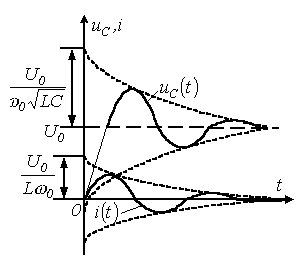
5.5 Сурет
№6 дәріс 6. Конденсатордың периодтық (тербелістік) разряды., R, L,C тізбектерінің тұрақты және синусоидалы кернеуге қосылуы
6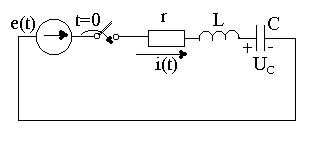
.1-сурет. r, L, C тізбекті e(t) кернеуге қосу
r, L, C тізбек e(t) ЭҚК-ке қосылғанда (6.1-сурет) өтпелі процесс (6.1) дифференциалды теңдеу бойынша зерттеледі
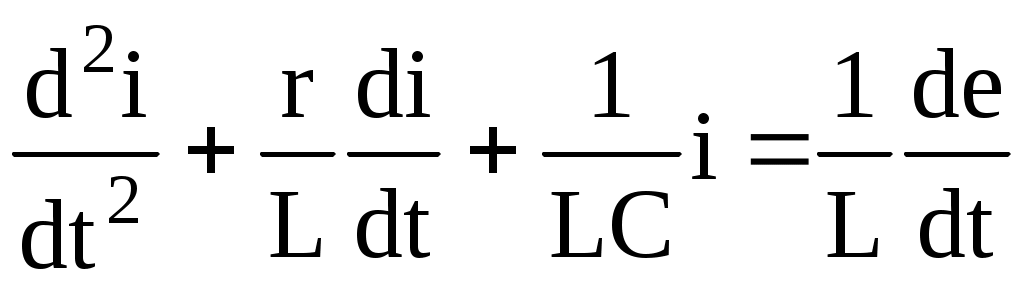 . (6.1)
. (6.1)
Бұған сәйкес сипаттамалы теңдеу
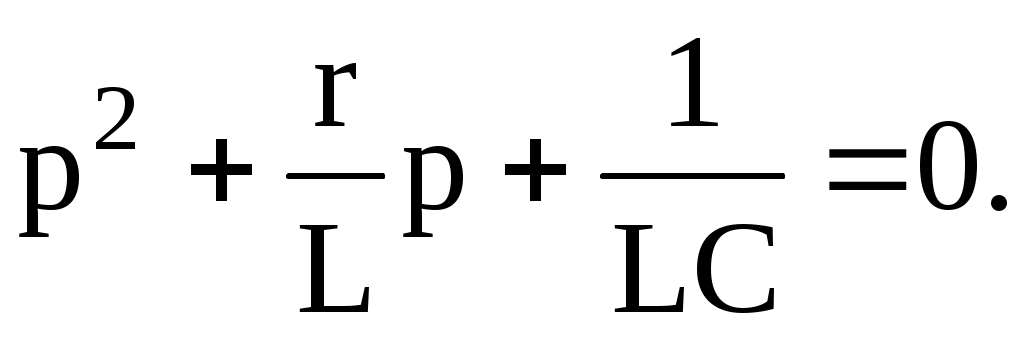
Оның түбірлері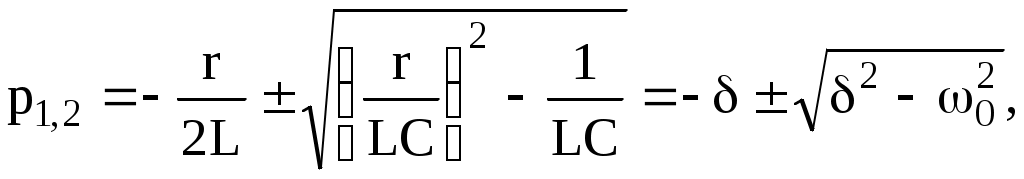 (6.2)
(6.2)
мұнда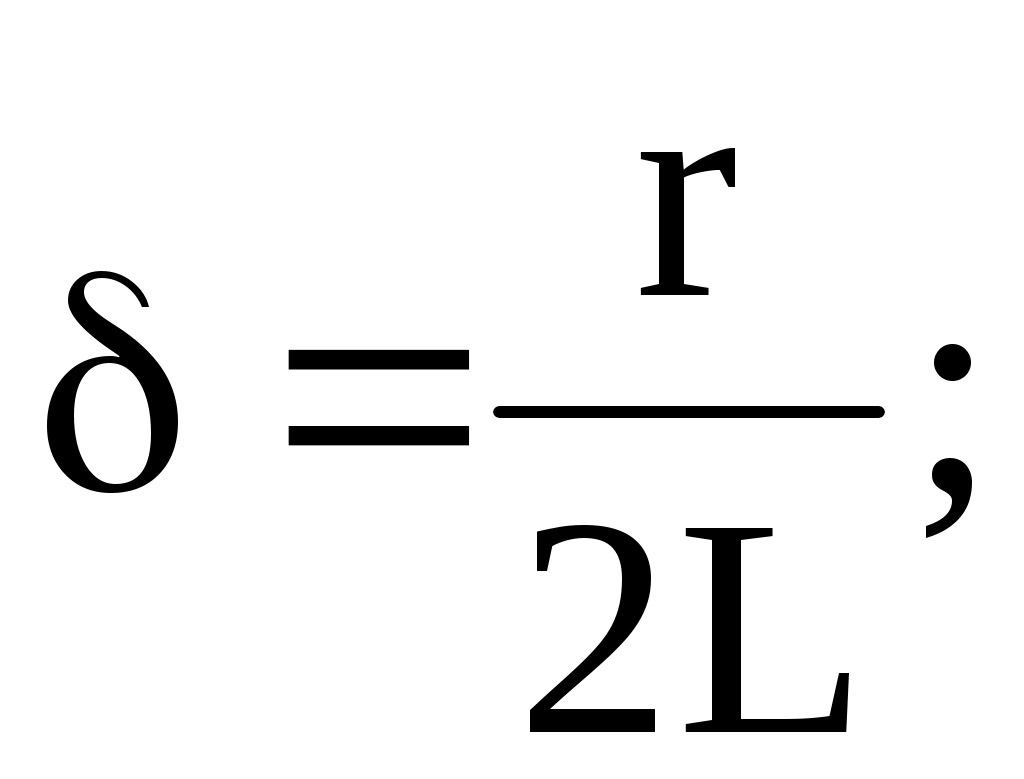
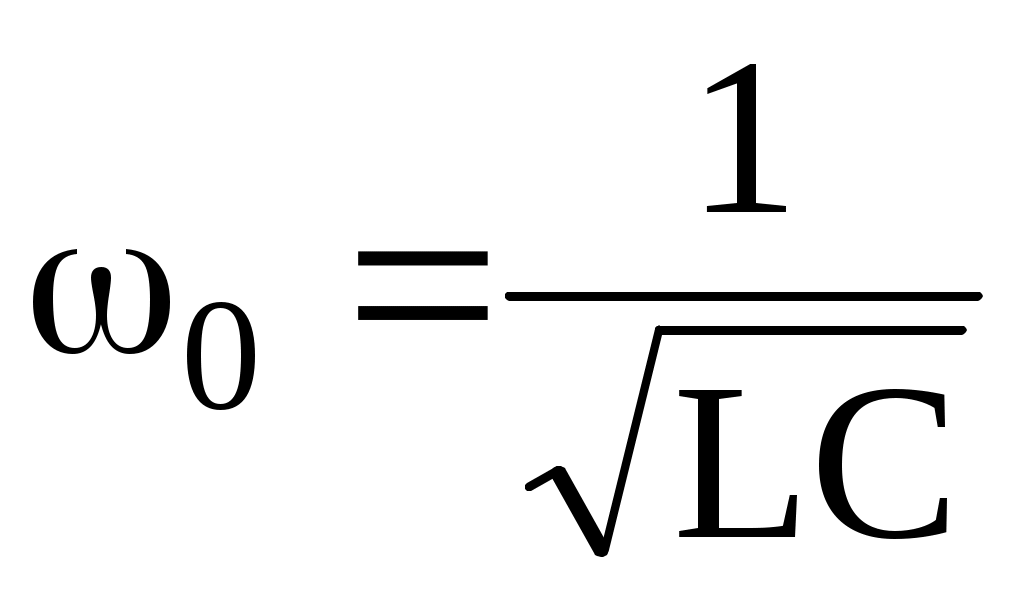 -резонансты жиілік бойынша
-резонансты жиілік бойынша 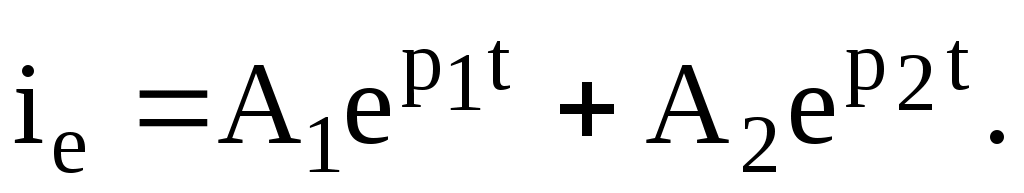
Тізбектегі ток қалыптасқан және еркін токтардың қосындысы.
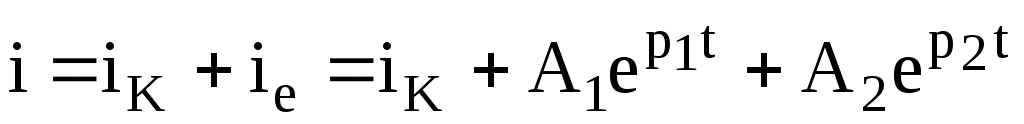 . (6.3)
. (6.3)
Қалыптасқан ток берілген e(t) ЭҚК-ке сәйкес табылады, ал еркін токтың түрі (7.3) көрністің (түбір астындағы) таңбасына тәуелді.
6.1 r, L, C тізбекті тұрақты ЭҚК-ке қосу
Сыйымдылықтың басты кернеуі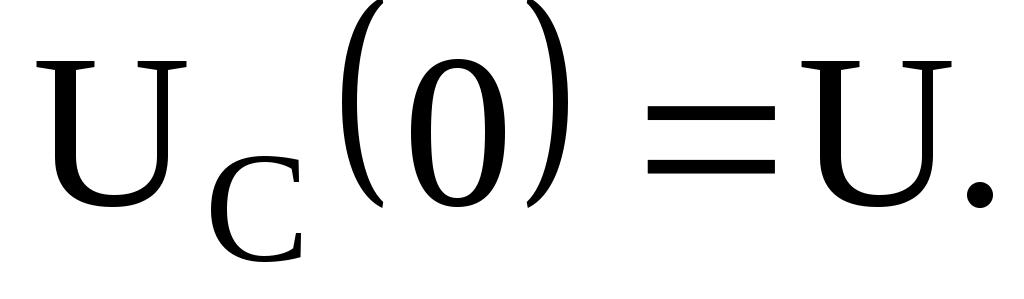
Тізбекте индуктивтік болғандықтан токтың басты мәні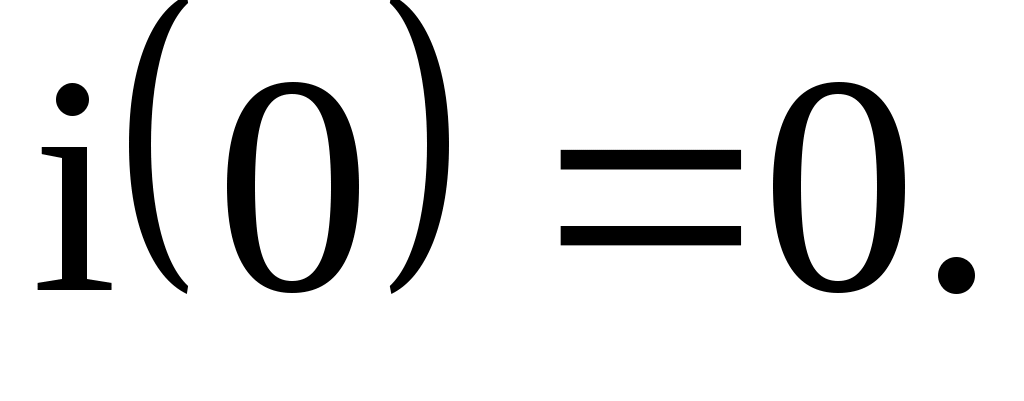
Бастапқы теңдеуі
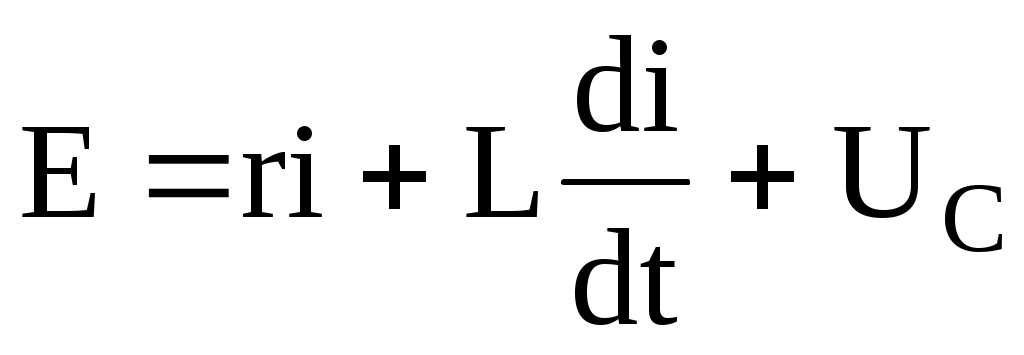 .
.
Коммутация басталған кездегі түрі мынадай болады
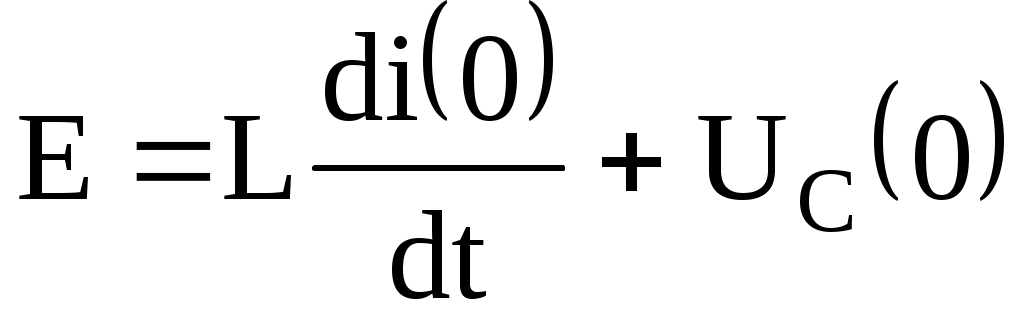 (6.4)
(6.4)
(7.4) теңдеуден табамыз
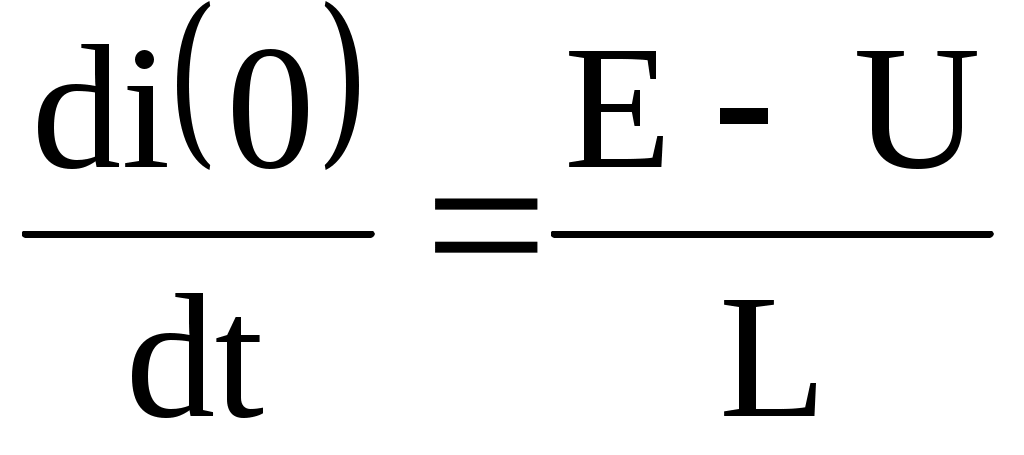 (6.5)
(6.5)
iҚ ток тұрақталған ереже кезде нөлге тең, сол себептен (6.3) теңдеуді дифференциалдаудан кейін шығады
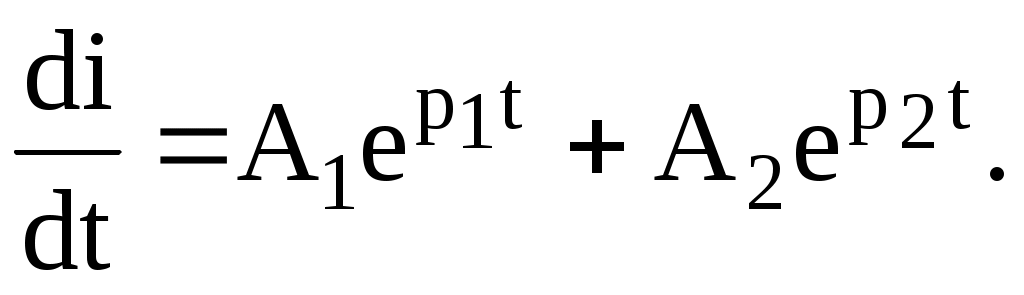 (6.6)
(6.6)
(6.3) және (6.6) теңдеулерге және (6.5) пайдаланып t=0 уақыт үшін жазамыз:
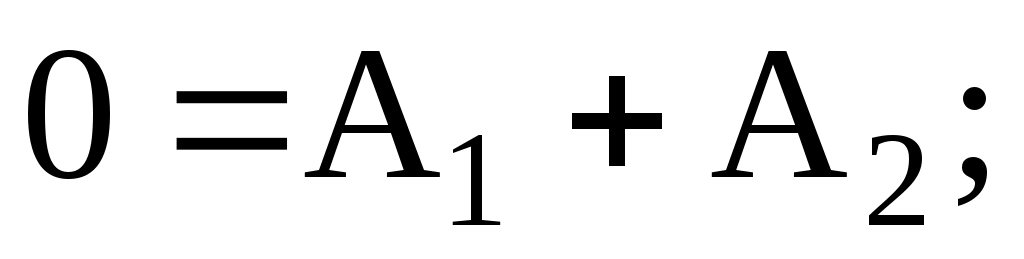
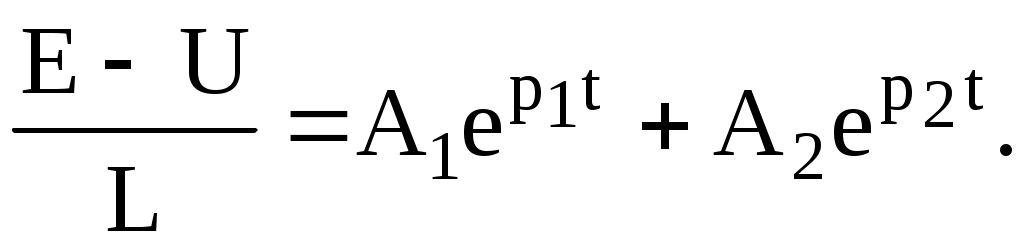
Бұл теңдеулерден шығады:
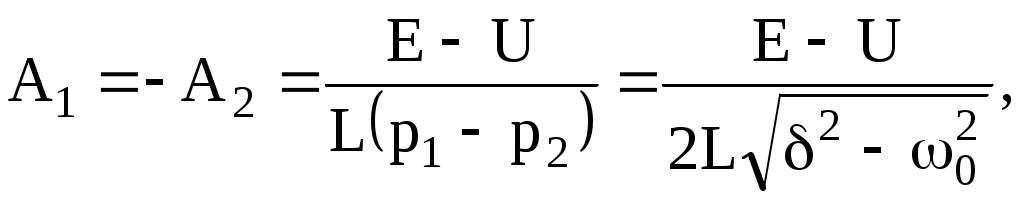 сондықтан
сондықтан
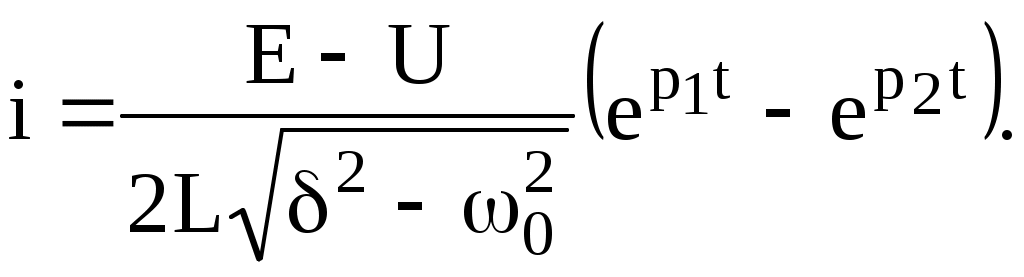 (6.7)
(6.7)
Мүмкін болатын үш жағдайды қарап шығамыз:
1 жағдай.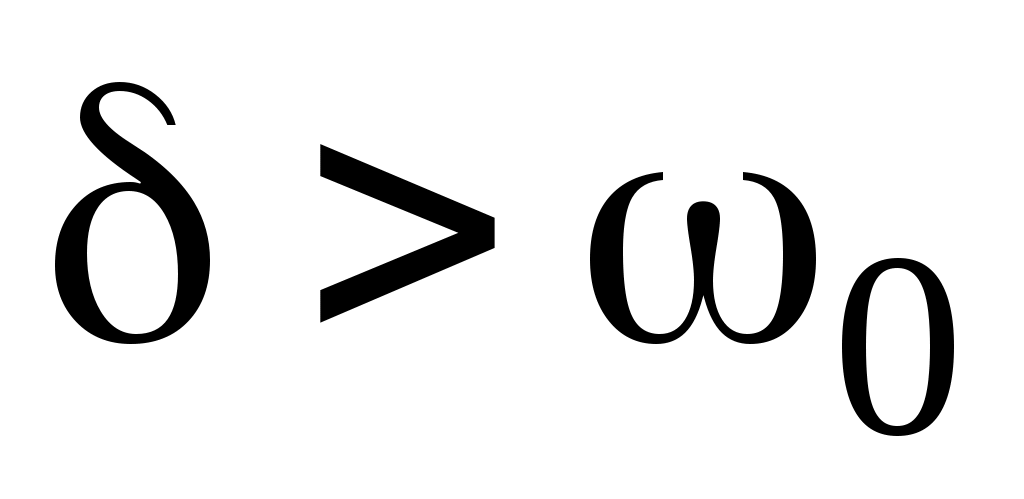 , яғни
, яғни 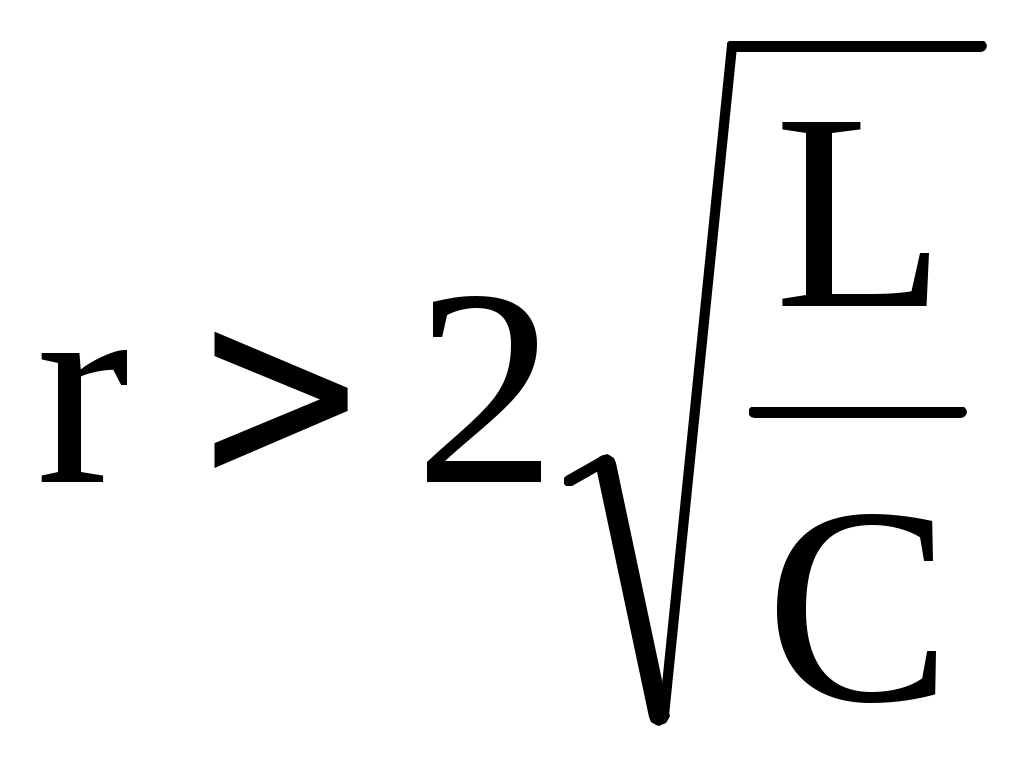 (апериодикалы процесс).
(апериодикалы процесс).
(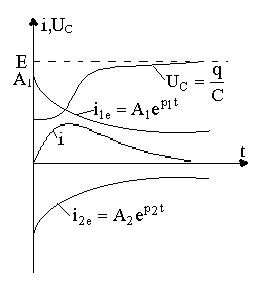
6.2) бойынша сипаттамалы теңдеудің түбірлері p1 және p2-теріс нақтылы сандар.
6.2-сурет. r, L, C тізбектегі апериодикалы процесс
2 жағдай 0, яғни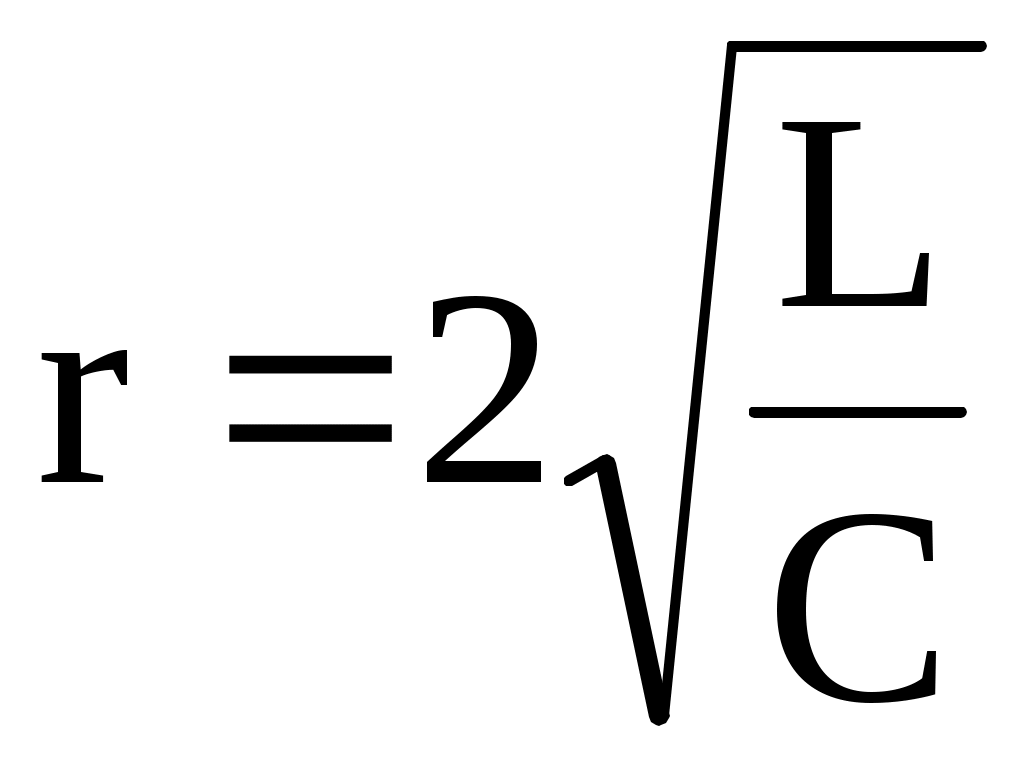 (7.2) бойынша
(7.2) бойынша 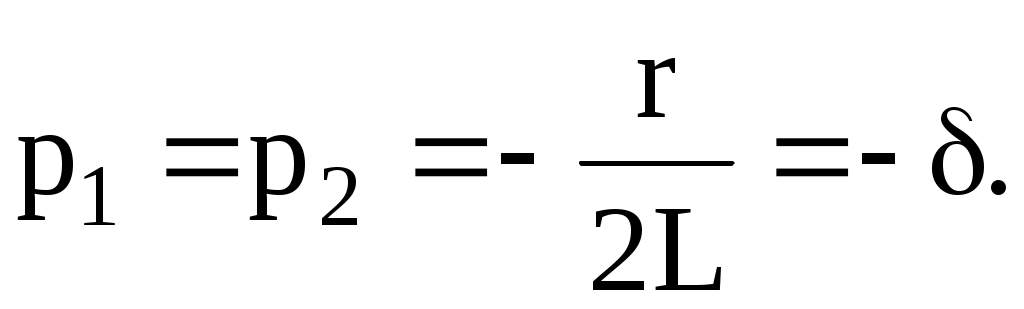 Бұл жағдайда (7.7) теңдеу түрі
Бұл жағдайда (7.7) теңдеу түрі 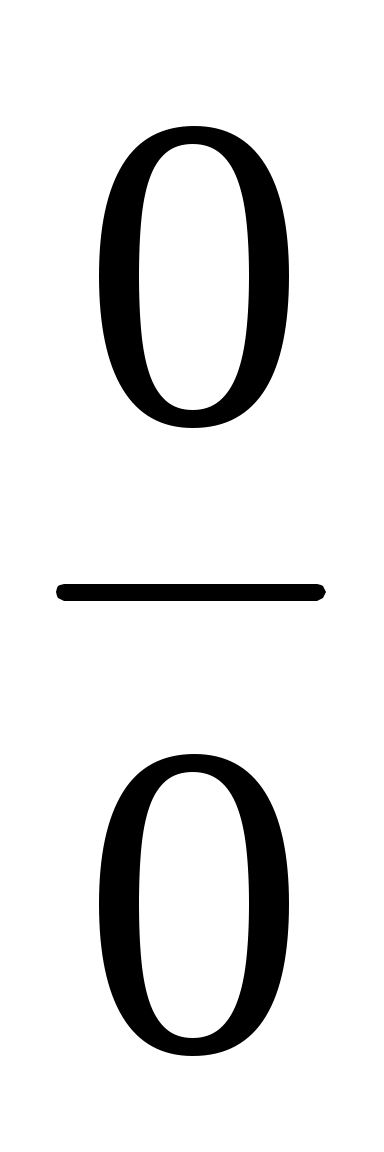 белгісіздікке әкеледі. Белгісіздікті Лопитальдың тәртібі бойынша ашқанда шығады
белгісіздікке әкеледі. Белгісіздікті Лопитальдың тәртібі бойынша ашқанда шығады
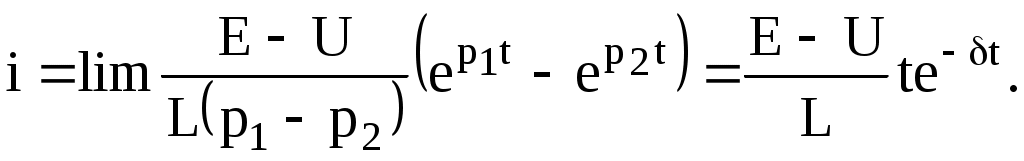
Токтың қисығы 8.11-суреттегі i қисығына сәйкес.
3 жағдай. <0, яғни
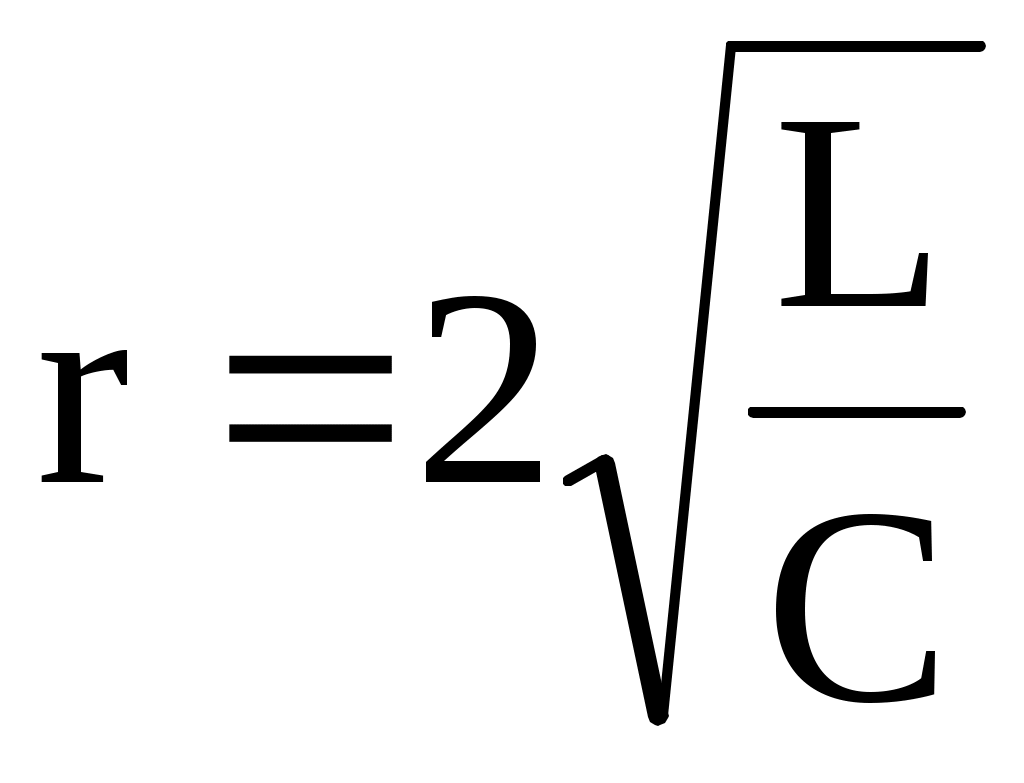 (тербелу процесі).
(тербелу процесі).
Сипаттамалы теңдеудің түбірлері комплексті және ілестіру
6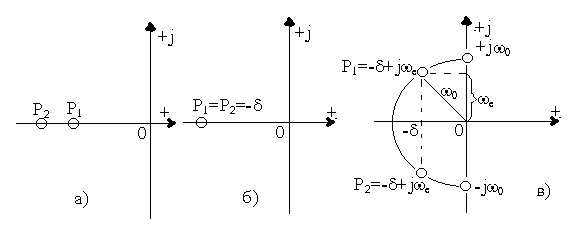
.3-сурет. Сипаттамалы теңдеудің түбірінің коиплексті жазықтықта орналасуы
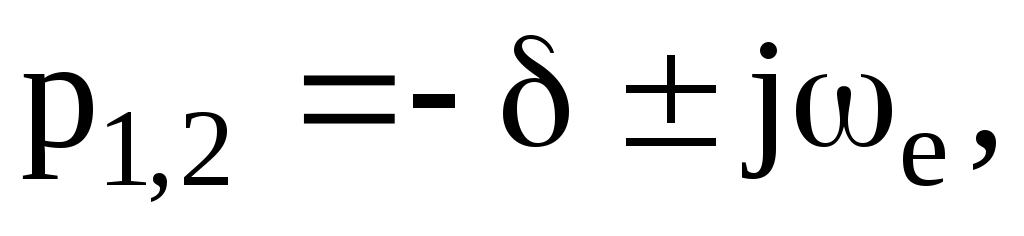 мұнда
мұнда 
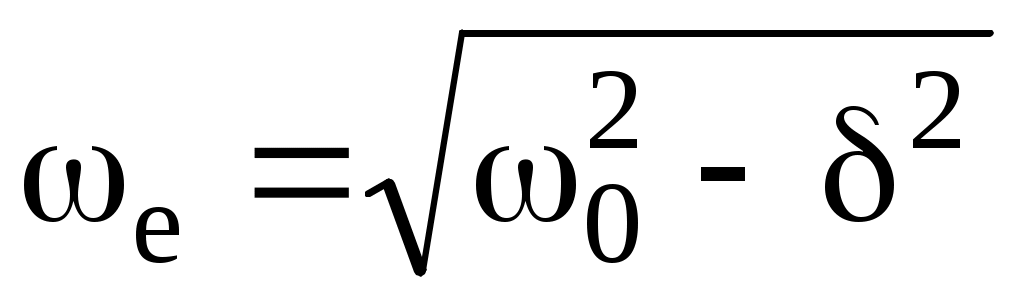
Сипаттамалы теңдеудің түбірлері нақтылы білікке симметриялы сол жартылай жазықтықта жартылай шеңбердің үстінде орналасады. Шеңбердің орталығы координат басында, ал радиус тең
Тізбектегі ток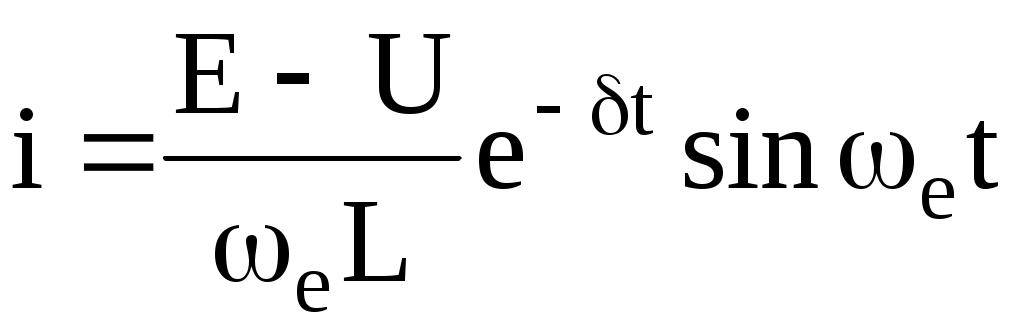
Сонымен, r, L,C тізбекті тұрақты кернеуге қосқанда, егер де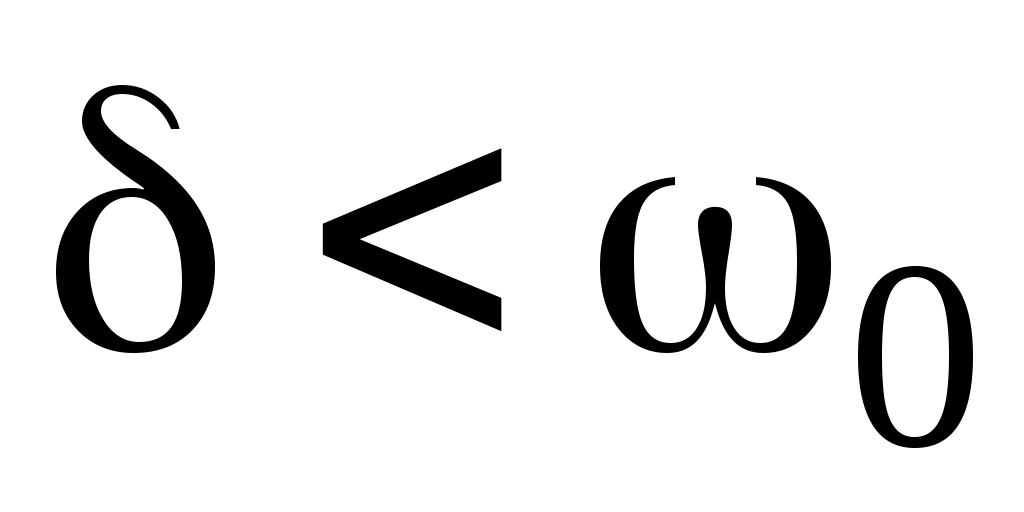 болса тізбекте сөнетін синусоидалды тербелу пайда болады. Токтың қисығын оралып өтетін қисықтар
болса тізбекте сөнетін синусоидалды тербелу пайда болады. Токтың қисығын оралып өтетін қисықтар 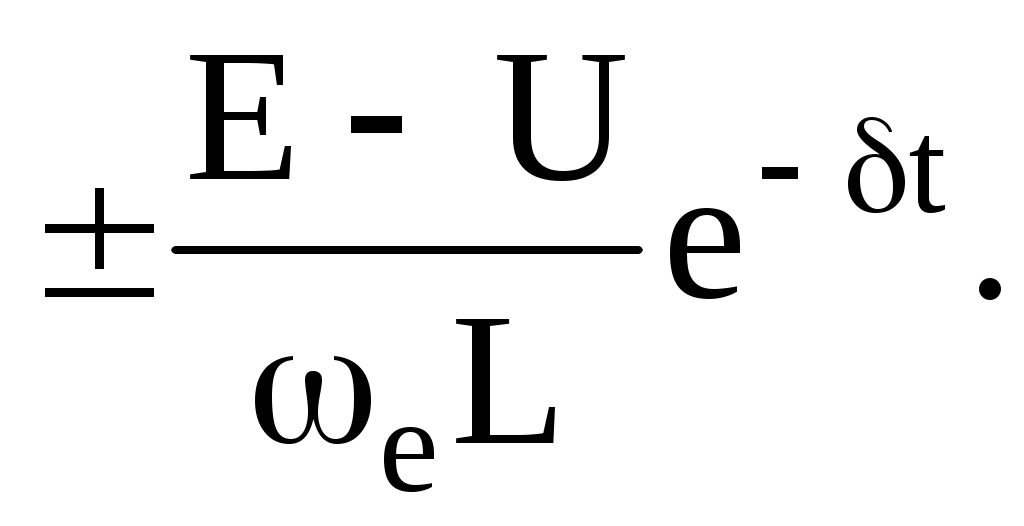 Тербелу пайда болу себеп-электр өрістің энергиясын магнит өрістің энергиясына периодты түрлендіру және кері өтетін процесс, бұл тербелулер кедергіде энергия шығындармен өтеді, яғни
Тербелу пайда болу себеп-электр өрістің энергиясын магнит өрістің энергиясына периодты түрлендіру және кері өтетін процесс, бұл тербелулер кедергіде энергия шығындармен өтеді, яғни
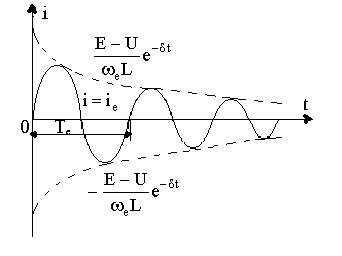
6.4-сурет. r, L, C тізбектегі ЭҚК-ке қосқанда тербелу процесс
тербелу өшеді.
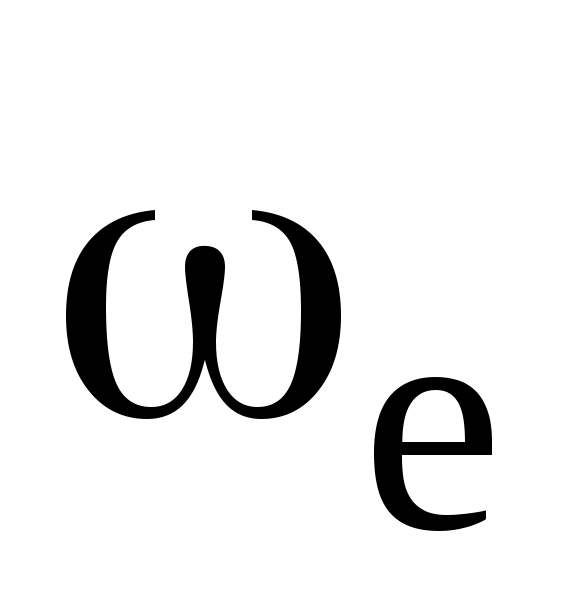 шама (6.3, в-сурет) көрсетіп тұр-r, L, C тізбектегі еркін немесе өздік тербелудің бұрыштық жиілігі деп, ал
шама (6.3, в-сурет) көрсетіп тұр-r, L, C тізбектегі еркін немесе өздік тербелудің бұрыштық жиілігі деп, ал 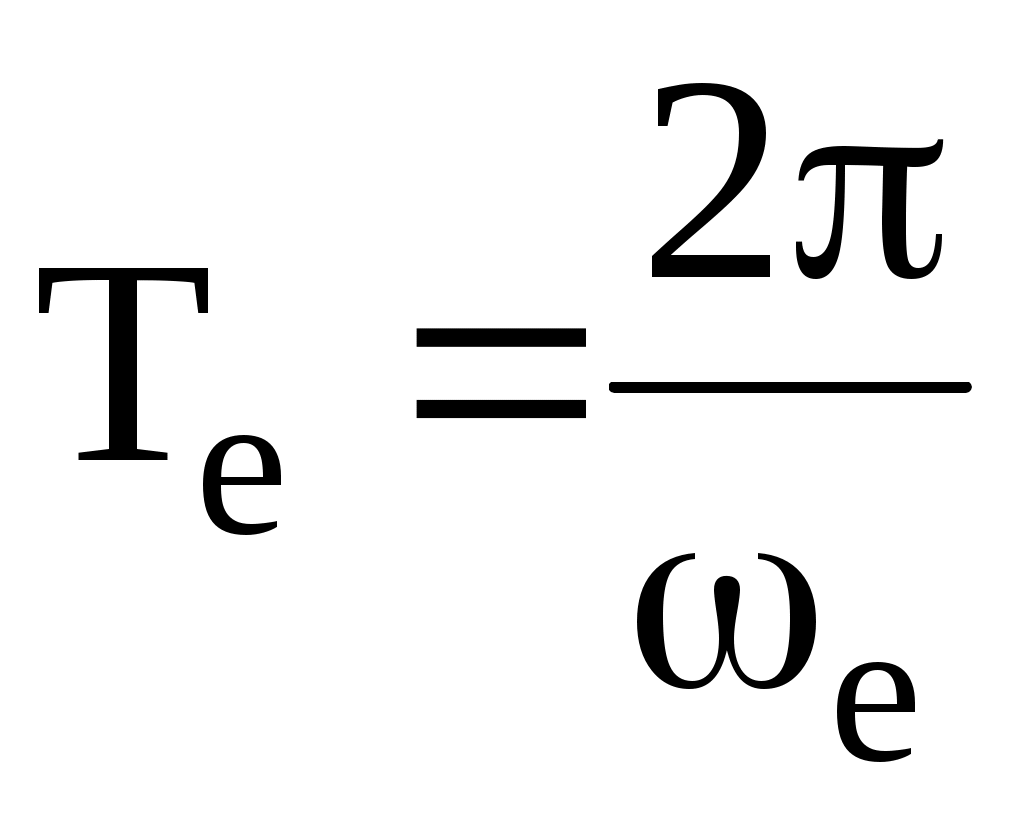 -бұл тербелудің периоды деп атайды.
-бұл тербелудің периоды деп атайды.
6.5, а, б, в-сурет көрсетіп тұр-r, L, C тізбектегі өтпелі процестің түрі туралы сипаттамалы теңдеудің түбірлерінің орналасуы бойынша айтуға болады, яғни Z(p) функциясының комплексті жазықтықта нөлдер бойынша.
Сәйкесінше разрядты тоқ
-
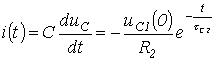 .
.
(5.5)
Өтпелі кезеңде RLC- тізбегін кернеу көзіне тізбектей .
Мына жағдайды қарастырайық
Алдыңғы дәрісте қарастырғандай өтпелі кезеңдегі классикалық әдісті конденсатордағы кернеуді 3.3 суретіндегі тізбекке қарап былай жазуға болады.
| | (5.7) |

6.3 Сурет
| Бірінші жағдай үшін мына кернеудің еріксіз құраушысы | (5.8) |
Тізбектің сипаттамалық теңдеуі
Осыны шешіп, келесіні аламыз
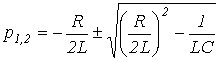 .
.Тізбек көрсеткіштерінің арақатынасына байланысты үш түбір болуы мүмкін және еркін құрастырушылар үшін үш нұсқа қарастырамыз:
1.
| Осыдан | (5.9) |
2.
Осы жағдайда
| | (5.10) |
3.
Осы жағдайда
| | (5.11) |
мұндағы
- өздік тербелістің периоды.
Өтпелі кезеңнің периодикалық емес сипаттамасы үшін мынаны жазуға болады:
Интегралдау тұрақтысын табу үшін, жалпы жағдайда
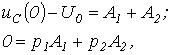
Осыны шешіп, келесіні аламыз
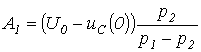 ;
; 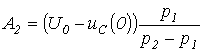 .
.Сондықтан,
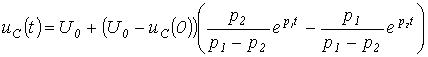 .
.Сонда тізбектің тоғы
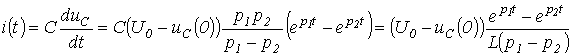
орамадағы индуктивті кернеу
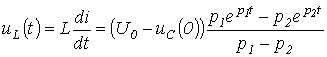 .
.5.4 суретінде , және сапалы кедергілер берілген, периодикалық емес өтпелі кезеңге қатысты.

5.4 Сурет
Критикалық ереже үшін былай жазуға болады.
болағанда
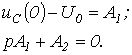
Сондықтан,
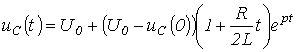
және
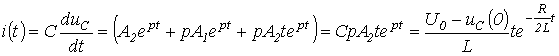 .
.Тербелмелі өтпелі ереже үшін
Интегралдау тұрақтысын табу үшін
Осыдан
сонда
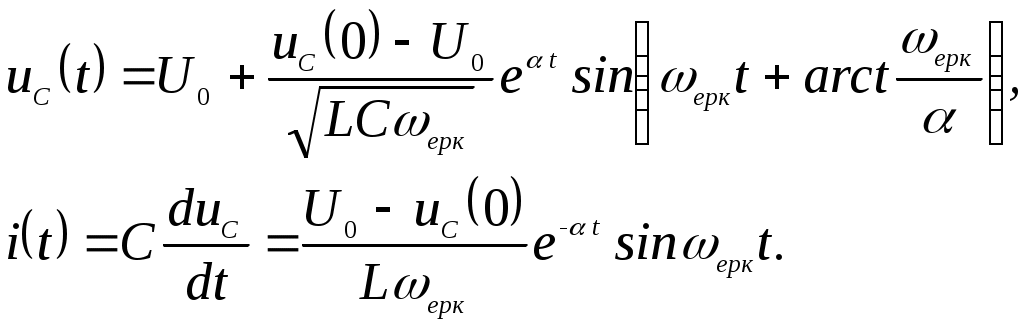
5.5 суретте

5.5 Сурет
№6 дәріс 6. Конденсатордың периодтық (тербелістік) разряды., R, L,C тізбектерінің тұрақты және синусоидалы кернеуге қосылуы
6

.1-сурет. r, L, C тізбекті e(t) кернеуге қосу
r, L, C тізбек e(t) ЭҚК-ке қосылғанда (6.1-сурет) өтпелі процесс (6.1) дифференциалды теңдеу бойынша зерттеледі
Бұған сәйкес сипаттамалы теңдеу
Оның түбірлері
мұнда
Тізбектегі ток қалыптасқан және еркін токтардың қосындысы.
Қалыптасқан ток берілген e(t) ЭҚК-ке сәйкес табылады, ал еркін токтың түрі (7.3) көрністің (түбір астындағы) таңбасына тәуелді.
6.1 r, L, C тізбекті тұрақты ЭҚК-ке қосу
Сыйымдылықтың басты кернеуі
Тізбекте индуктивтік болғандықтан токтың басты мәні
Бастапқы теңдеуі
Коммутация басталған кездегі түрі мынадай болады
(7.4) теңдеуден табамыз
iҚ ток тұрақталған ереже кезде нөлге тең, сол себептен (6.3) теңдеуді дифференциалдаудан кейін шығады
(6.3) және (6.6) теңдеулерге және (6.5) пайдаланып t=0 уақыт үшін жазамыз:
Бұл теңдеулерден шығады:
Мүмкін болатын үш жағдайды қарап шығамыз:
1 жағдай.
(

6.2) бойынша сипаттамалы теңдеудің түбірлері p1 және p2-теріс нақтылы сандар.
6.2-сурет. r, L, C тізбектегі апериодикалы процесс
2 жағдай 0, яғни
Токтың қисығы 8.11-суреттегі i қисығына сәйкес.
3 жағдай. <0, яғни
Сипаттамалы теңдеудің түбірлері комплексті және ілестіру
6

.3-сурет. Сипаттамалы теңдеудің түбірінің коиплексті жазықтықта орналасуы
Сипаттамалы теңдеудің түбірлері нақтылы білікке симметриялы сол жартылай жазықтықта жартылай шеңбердің үстінде орналасады. Шеңбердің орталығы координат басында, ал радиус тең
Тізбектегі ток
Сонымен, r, L,C тізбекті тұрақты кернеуге қосқанда, егер де

6.4-сурет. r, L, C тізбектегі ЭҚК-ке қосқанда тербелу процесс
тербелу өшеді.
6.5, а, б, в-сурет көрсетіп тұр-r, L, C тізбектегі өтпелі процестің түрі туралы сипаттамалы теңдеудің түбірлерінің орналасуы бойынша айтуға болады, яғни Z(p) функциясының комплексті жазықтықта нөлдер бойынша.