және болғанда әрбір тармақта сыртқы ЭҚК Е_К(р)-дан басқа ішкі ЭҚК-тер L_Ki_K(0) және U_CK(0)/p әсер етеді (олардың болымды бағыттары сол тармақтағы токтың болымды бағытына сәйкес), екінші-тармақтың кедергісі ретінде операторлық кедергі алынады.


№9 дәріс 9. Балама операторлық сұлбалар. Өтпелі кезендерді операторлық есептеу жалпы жағдайы.
9.1 Балама операторлық сұлбалар.
Операторлық әдіспен өтпелі процесті есептеген кезде берілген тізбек үшін баламалы операторлық схеманы құру пайдалы болады.





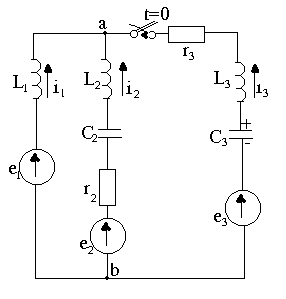
9.1-сурет. Тізбектің электр схемасы




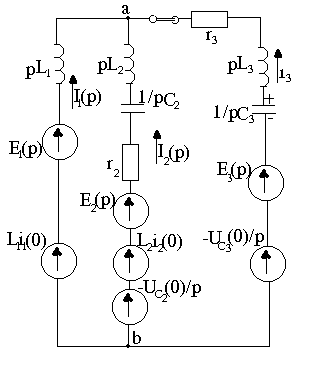
9.2-сурет. Тізбектің баламалы операторлық сүлбесі
Басты жағдайлар нөлге тең болмағанда баламалы операторлық схеманы құруды 10.2-суретте келтірілген схеманы қарайық.
Киргофтың заңдарын операторлық түрде жазамыз:





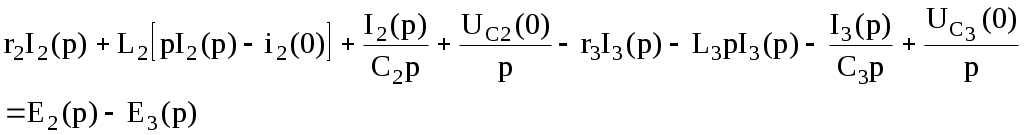Қайтадан мына түрде жазамыз: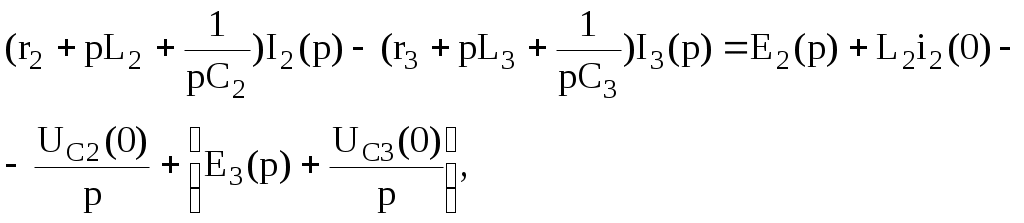







бұл теңдеулер бойынша 10.2-суретте келтірілген балама операторлық схеманы құрамыз.

Тізбектерді есептеу әдістердің бәрі де Киргофтың теңдеулерінен шығарылатын себептен, токпен кернеудің кесінділерін есептеу үшін (9.3-сурет) контурлық ток, түйінді потенциалдар және т. б. әдістерді қолдануға болады.
№10 дәріс 10. Төртұштықтар және оның негізгі теңдеуі.
Дәрістің мақсаты: төртұштықтардың және сүзгілердің негізгі түсініктемелерін қарастыру.

---

Төртұштық деп екі кірістік және екі шығыстық қысқыштары бар электрлі сұлба аталады. Трансформатор, энергия беріліс желісі, көпірше сұлбасы және т.б. төртұштық ретінде қарастырыла алады.

Төртұштық тіктөртбұрыш түрінде көрсетіледі, одан төрт ұшы (полюстері) тп және рд (10.1,а суретті қара) шығып тұрады. Егер төртұштықтың құрамында электр энергия көздері болса, онда тіктөртбұрыштың ішінде А әріпі жазылады, төртұштвқ бұл жағдайда активті деп аталады; егер А әріпі жоқ болса, онда төртұштық пассивті болып саналады.





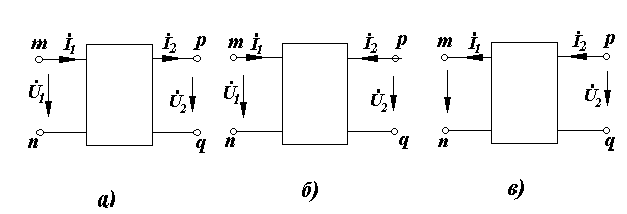
10.1 сурет- Төртұштық сұлбасы
Төртұштықтың кірісіндегі ток İ₁, кірістік кернеу U₁; шығысындағы ток пен кернеу İ₂ , U₂деп белгіленеді.

Төртұштық қорек көзі мен жүктеме арасындағы байланыс тармақ болып табылады. Төртұштықтың кірістік шықпаларына қорек көздерін қосады, ал шығыстық шықпаларына жүктемелер қосылады.

Төртұштықтың жұмыс істеуі кезінде, оның жүктемесі және шығысындағы кернеуі байланыс тармағы ретінде өзгере алады, дегенмен ішкі жалғанулар сұлбасы және ондағы кедергілерінің мәндері өзгеріссіз қалады деуге болады.

Төртұштық екі кернеу U₁, U₂және екі ток İ₁,İ_2.шамаларымен сипатталады. Төрт шаманың кез келген екеуін, қалған екеуі арқылы анықтауға болады. Төрт шаманың екі-екіден үйлесу саны 6 болғандықтан, пассивті төртұштық теңдеулерінің 6 түрін ажыратуға болады.

A- түрі: , .	(10.1) (10.2)
Y- түрі: , .	(10.3) (10.4)
Z- түрі: , .	(10.5) (10.6)
H- түрі: , .	(10.7) (10.8)
G- түрі: , .	(10.9) (10.10)
B- түрі: , .	(10.11) (10.12)

---

Берілген теңдеулерден Y пен Z, A мен B, H пен G түрлері ұқсас екендігіне көз жеткізуге болады.

Төртұштық теңдеуінің А-түрі үшін (негізгі түрі) кернеулер мен токтардың оң бағыттары 11,1, а суретіндегідей, Y, Z, H, G түрлері үшін- 10,1, б суретіндегідей, В –түрі үшін- 10,1, в суретіндегідей қабылданады.

Өзаралық шартына қанағаттанатын төртұштықтардың коэффициенттері келесі сәйкестікпен байланысты:
АD-ВС=1. (10.13)

Төртұштықтың қорек көзінің және жүктеменің орын ауыстыруы кезінде, қорек көзіндегі және жүктеменің токтары өзгермеген жағдайда төртұштық симметриялы деп аталады. Симметриялы төртұштықта A=D. теңдеуін кейбір жағдайларда келесі түрде жазады:

=A₁₁ +A₁₂İ_2,,

İ₁=A₂₁ +A₂₂İ₂,

мұндағыA₁₁= A; A₁₂=В; A₂₁= С; А₂₂=D.

Ажәне D коэффициенттерінің өлшем бірлігі болмайды, Bкоэффициентінің өлшем бірлігі Ом, С коэффициентінің өлшем бірлігі См.

---

10.2 Төртұштықтардың еселеуішін анықтау. Төртұштықтардың балама сұлбалары.

Кернеу көзі мен жүктеме арасындағы беріліс тармақ ретіндегі пассивті төртұштықтың функциясын Т-сұлба (10.1, а суретіндегі сұлба) немесе оған баламалы П-сұлба (10.1, б сұлба) орындай алады.  жиілік бекітілген деп қабылданады. Т- немесе П- сұлбаның үш кедергісі, алмастыру сұлбасы, алмастрылған төртұштықтағыдай А,В, С,D коэффициенттеріне ие болу керектігін ескеріп есептеледі. Бұл есеп міндетті түрде орындалады, өйткені сұлбада үш элемент болады және төртұштық үш параметрмен сипатталады (А,В, С,D арасындағы бір байланыс АD-ВС= 1 теңдеуімен берілген).




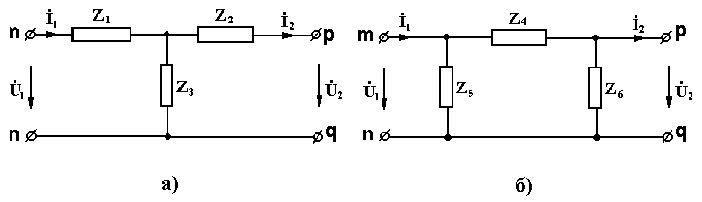
10.1 сурет- Төртұштықтың Т және П тәрізді алмастыру сұлбалары

Т-сұлбаның U₁ кернеуін және İ₁ тогын (10.1,а суретті қара) U₂ кернеуі мен İ₂ тогы арқылы өрнектейік:
, (10. 1)
. (10. 2)

(10. 1) өрнегін және (10.2) өрнегін сәйкестендірейік. нәтижесінде,

Z₁=(A-1)/C, Z₃=1/C, Z₂=(D-1)/C. (10.3)
(10.3) өрнектері төртұштықтың А, С, D коэффициенттері бойынша Z₁, Z₂, және Z₃, (10.1, а суретті қара) кедергілерін анықтауға көмектеседі. П-сұлба үшін (10.1, б суретті қара) ұқсас есептеулер келесі өрнектерді береді:
B=Z₄ , , (10. 4)

Z₄=B, (10.5)

Z₅=B/(D-1),(10.6)

Z₆=B/(A-1).(10.7)

Егер төртұштық симметриялы болса, онда А=D және Т-сұлбада Z₁=Z₂, ал П-сұлбада Z₅=Z₆болады.
10.3 Симметриялық төртұштықтардың сипаттамалық кедергісі және беріліс тұрақтысы.

---

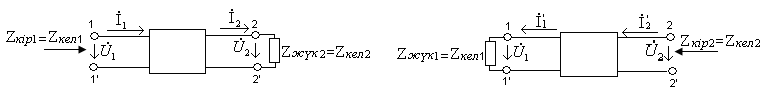а) б)

10.1 Сурет

Төртұштықтардың сипаттамалық кедергілері деп және , кедергілердің жұптары айтылады және ол мына шарттарды қанағаттандырады:

кезінде және кезінде (10.1а, 10.1,б - суреттер). - ні А – көрсеткіші және БЖ және КТ көрсеткіштері арқылы өрнектесек болады

, , (10.1)
, (10.2)

Симметриялы төртұштықтар үшін .

Төртұштықтарды келісім бойынша қосу

Егер, генератордың ішкі кедергісі -ге тең болғанда, жүктеменің кедергісі (10.2 - сурет) келісілген қосу тәртібі деп айтылады. Келісілген қосу тәртібі сигналдарды тасымалдағанда қолайлы.



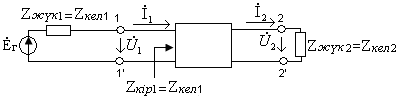
10.2 Сурет

Симметриялы төртұштықтың келісімді қосылу тәртібі (10.3 - сурет) ; .



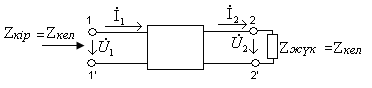
10.3 Сурет
10.4 Төртұштықтың тасымалдану тұрақтысының сипаттамасы.
Төртұштықтың тасымалдану тұрақтысының сипаттамасы қосылу тәртібі бойынша анықталады және тең болады

---

Смотрите также файлы

• Виды клизм Механизм действия.docx

• Гироскопический датчик Создание проекта.docx

• 1 общая характеристика объекта исследования.docx

• Тема Обеспечение реализации требований фгос к условиям реализации основных образовательных программ. Практическая работа 2.docx

• Swot анализ ооо Азбука Вкуса.docx