Файл: Учебное пособие Рыбинск 2007 удк 681. 5 Павлов Р. В. Основы теории управления. Учебное пособиергата. Рыбинск, 2007. 83 с.doc

Для определения критического значения добротности с помощью критерия Гурвица необходимо составить характеристическое уравнение системы. Для этого представим передаточную функцию (4) в виде отношения двух полиномов:

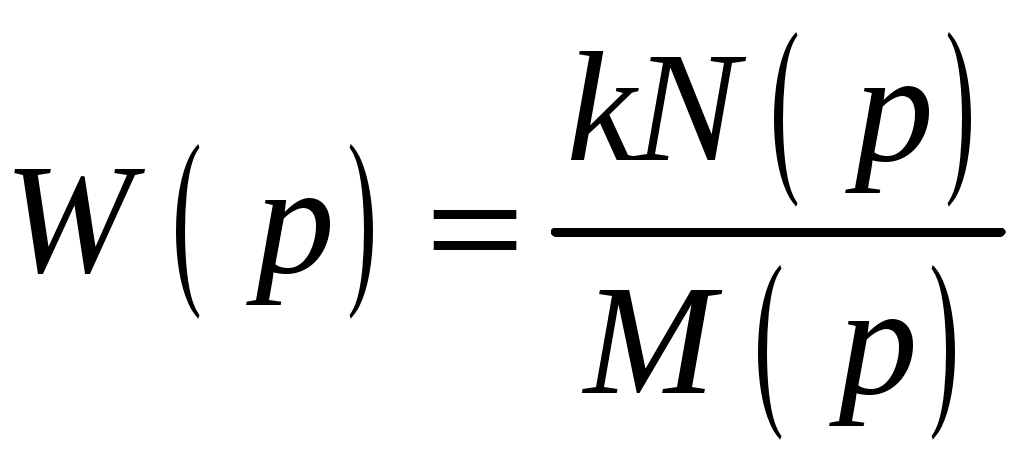, (5)

где k – общий коэффициент усиления разомкнутой системы, который часто называют добротностью системы;

– полином числителя;

– полином знаменателя.

При этом степень полинома в знаменателе больше, чем степень полинома в числителе.

Полиномы в выражении (5) имеют вид:

;

,

где коэффициенты

имеют следующие выражения:

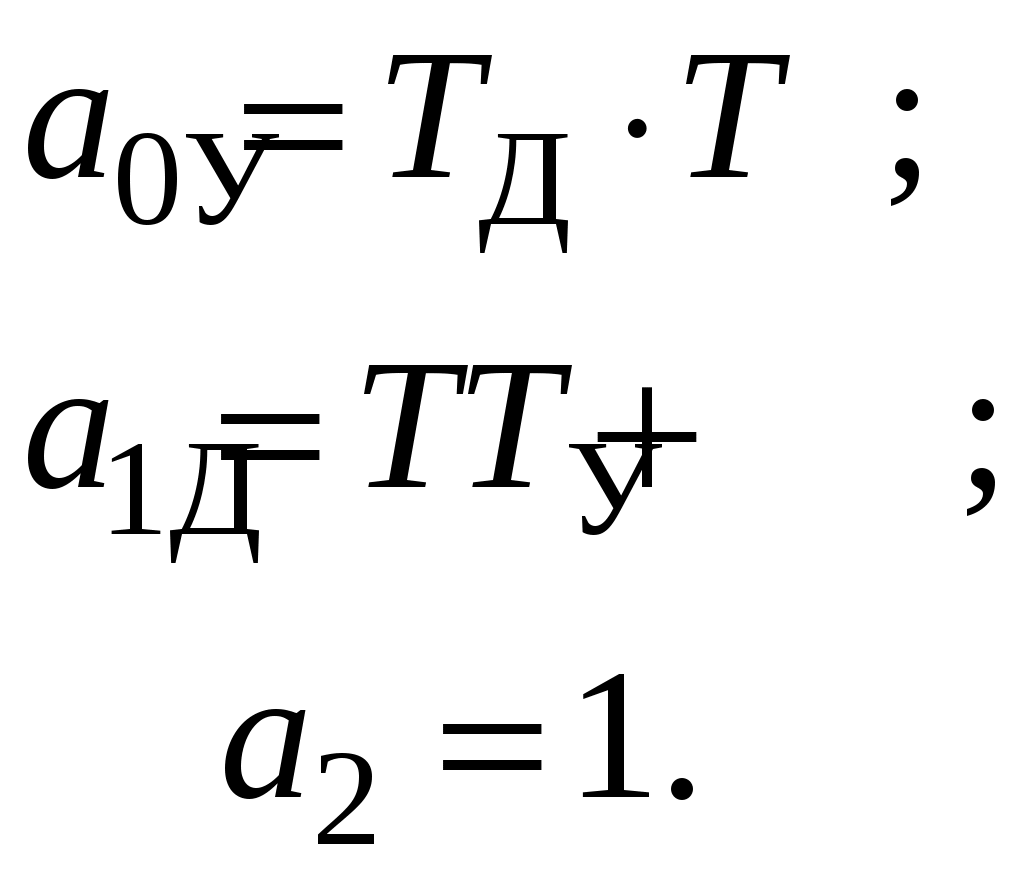
Далее запишем характеристический полином для выражения (5):

.

Приравняв его к нулю, получим характеристическое уравнение системы с передаточной функцией (4):

(6)

Это выражение можно записать и в более удобной форме:

(7)

Подставив значения полиномов в выражение (6), получим следующее характеристическое уравнение вида:

.

Критическое значение добротности

определим из критерия устойчивости Гурвица. Для уравнения 3-го порядка критерий устойчивости имеет следующие условия:

.

Из последнего условия и определим

.

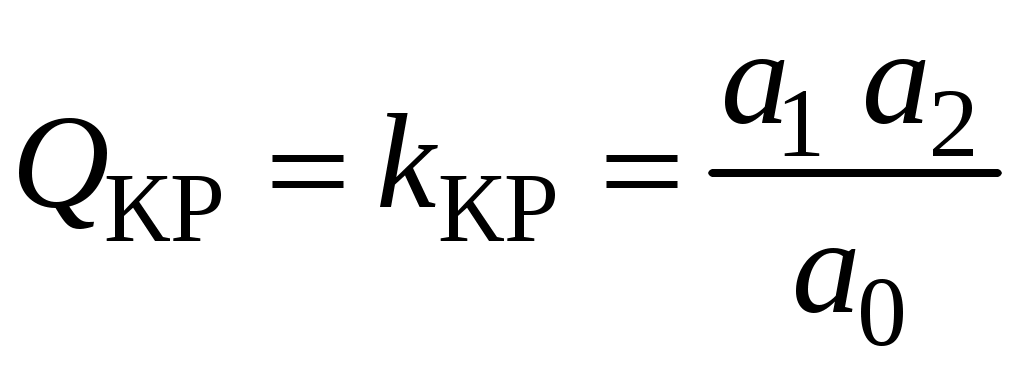Подставив выражения коэффициентов

, получим, что

;

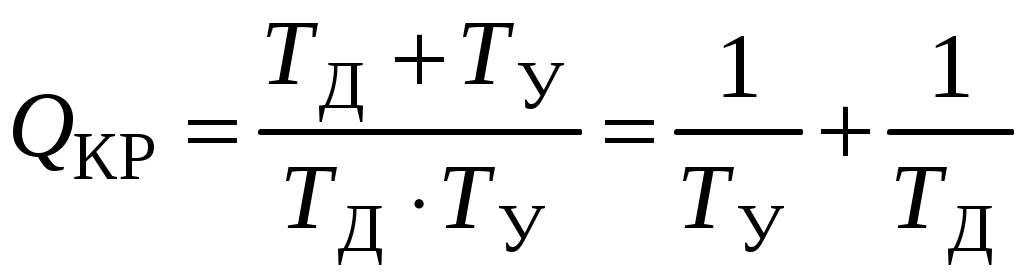Определив

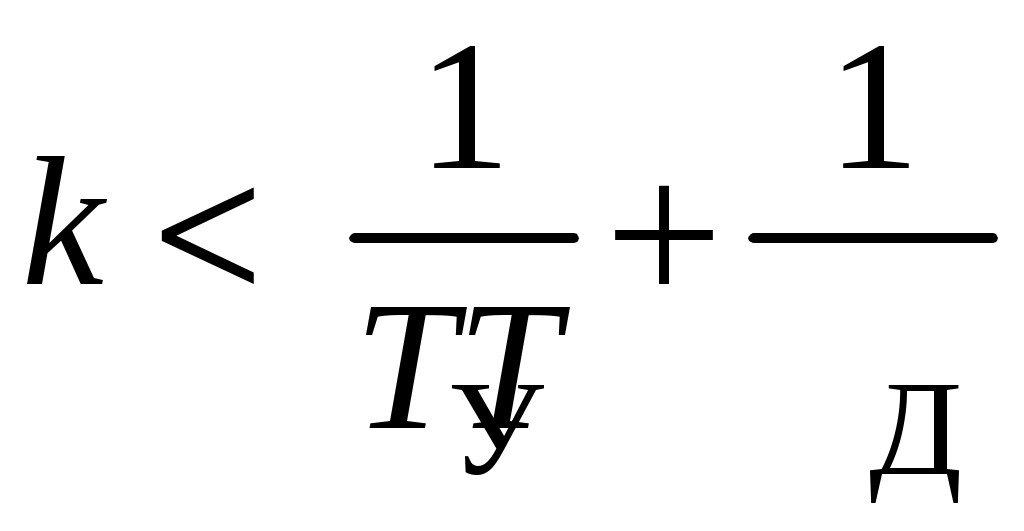, подтвердили, что наша система неустойчива, т. к.

. Для того, чтобы система была устойчива, необходимо выполнение условия:

11.8. Введение скоростной обратной связи

Для того чтобы исходную систему (см. задание) сделать устойчивой, необходимо дополнительно ввести местную отрицательную обратную связь. Воспользуемся скоростной обратной связью. Для введения скоростной обратной связи в систему включается дифференцирующее звено – тахогенератор (ТГ) согласно рис. 62.

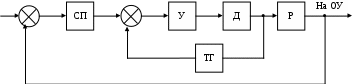
Рис. 62. Схема системы со скоростной обратной связью

Важным свойством скоростной обратной связи является способность уменьшать постоянные времени тех звеньев, которые она охватывает. Данная скоростная ОС охватывает 2 звена: усилитель и двигатель.

Перейдем к структурной схеме. Для этого найдем сначала передаточную функцию цепи скоростной обратной связи, т. е. передаточную функцию тахогенератора.

Так как тахогенератор – это дифференцирующее звено, то передаточная функция имеет вид:

,

где

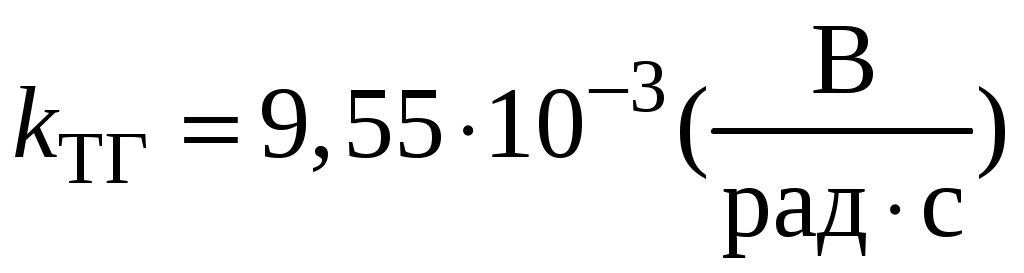– коэффициент передачи тахогенератора.

;

.

Структурная схема системы с отрицательной обратной связью будет иметь вид, приведенный на рис. 63.

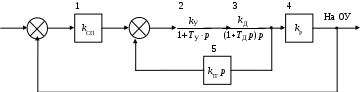
Рис. 63. Структурная схема системы с ОС

11.9. Нахождение минимального коэффициента
скоростной обратной связи

Для определения минимального коэффициента воспользуемся критерием устойчивости Гурвица. Но для этого сначала найдем результирующую передаточную функцию системы, представленной на рис. 63, и ее характеристическое уравнение. Эту передаточную функцию будем находить путем замены нескольких звеньев одним звеном с результирующей передаточной функцией для этих звеньев.

Заменим блоки 2 и 3 на блок 2-3 с передаточной функцией:

, т. к. блоки 2 и 3 соединены последовательно.

В результате замены получится следующая структурная схема (рис. 64).

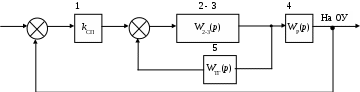
Рис. 64. Структурная схема системы с ОС после 1-го преобразования

Далее заменим блоки 2 – 3 и 5 одним блоком 2 – 3 – 5 с передаточной функцией:

,

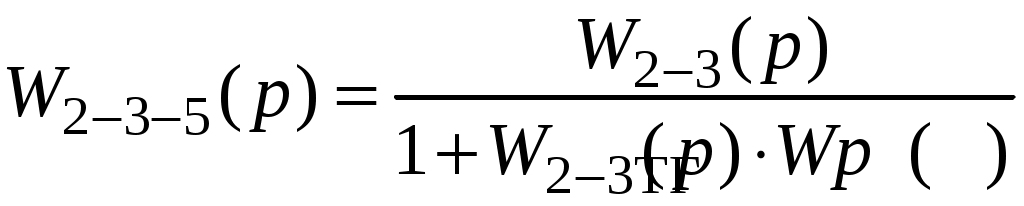т. к. блок 5 выполнен в виде обратной связи. В результате этой замены получим схему (рис. 65):

Рис. 65. Структурная схема системы с ОС после 2-го преобразования

Из этой схемы видно, что система состоит из трех последовательно соединенных звеньев, следовательно,

будет определяться следующим
образом:

Подставив выражения передаточных функций в эту формулу, получим:

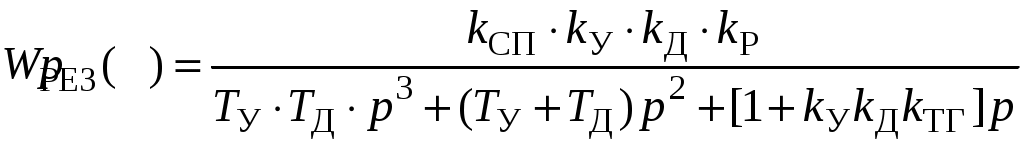. (8)

Далее находим характеристическое уравнение системы с передаточной функцией (8) по формуле (7). Полученное уравнение будет иметь вид:

.

Заменим коэффициенты в этом уравнении

.

Исходя из этого уравнения третьего порядка, определяем критерий устойчивости Гурвица. По критерию Гурвица система будет устойчива

, если будут выполняться следующие условия:

.

Из последнего условия и определяем минимальный коэффициент скоростной обратной связи

. Подставив в это условие выражения

и выделив

, получим:

.

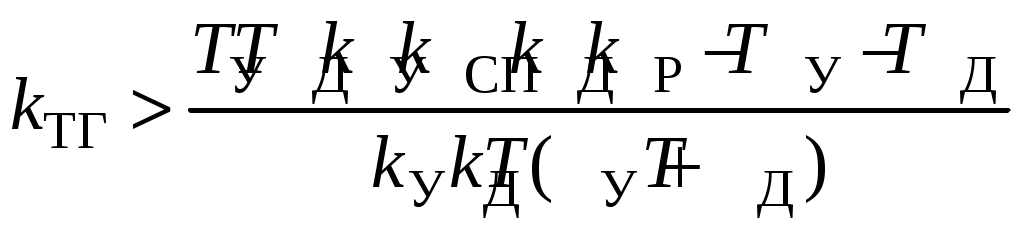Подставив значения переменных, получим:

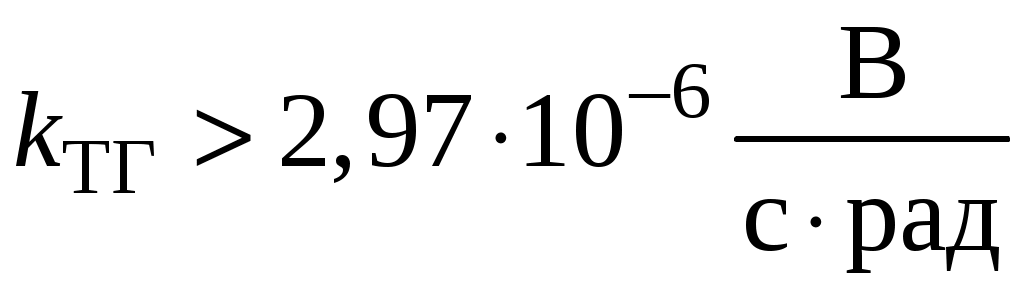, следовательно

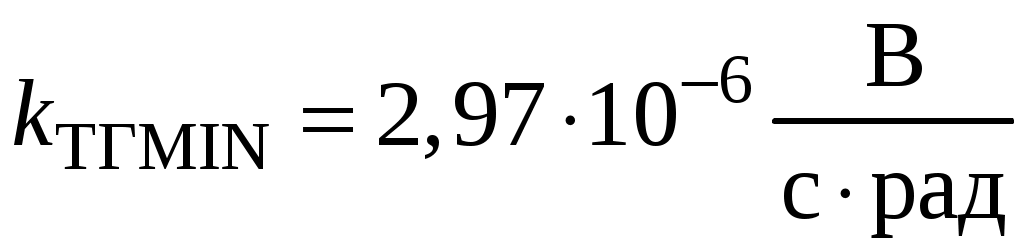11.10 Определение оптимального коэффициента
скоростной обратной связи

Это коэффициент, обеспечивающий требуемые показатели качества переходного процесса.

Воспользуемся корневым методом. Он позволяет учесть эти показатели качества, не исследуя сам переходный процесс, а накладывая ограничения на корни характеристического уравнения.

В примере уравнение третьего порядка. Его можно представить в
виде

,

где р₁, р₂, р₃ – корни характеристического уравнения.

Согласно методу, система склонна к колебаниям, если корни комплексные, т. е.

. Корень р₃ найдем через р₁ и р₂.

Коэффициенты α и β через показатели качества высчитываются следующим образом:

;

,

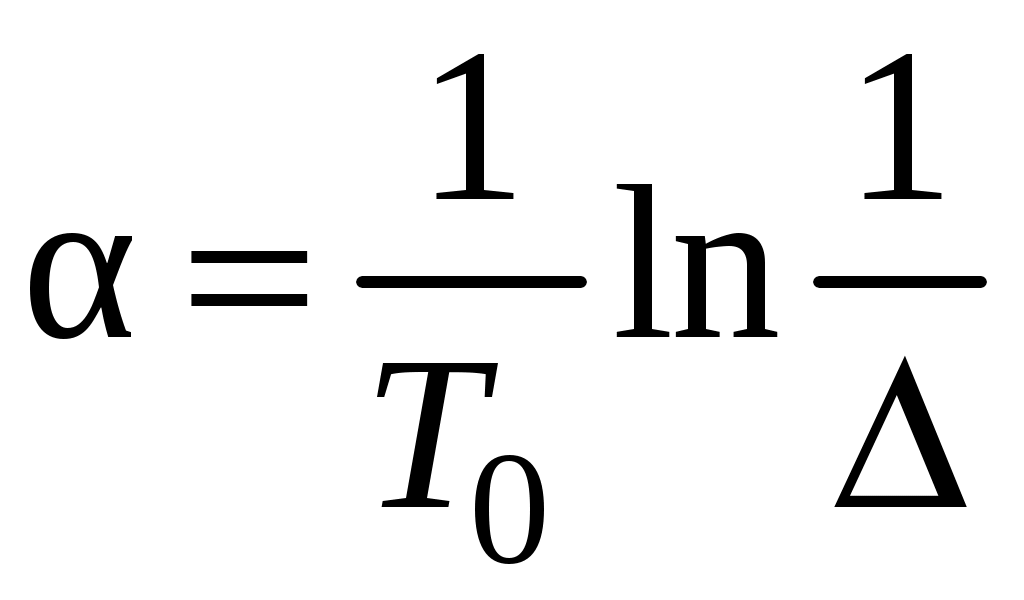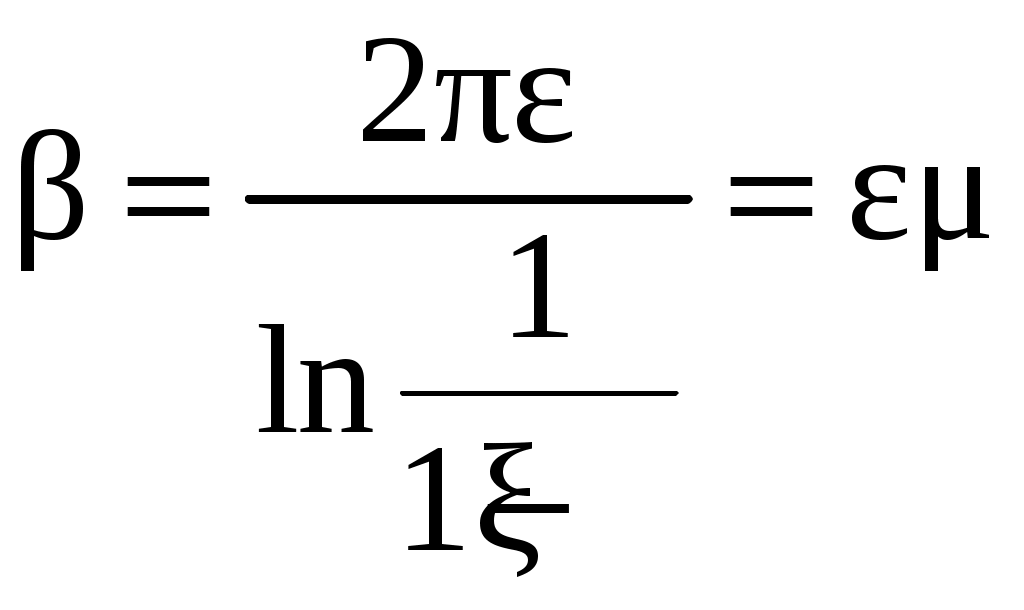где  – степень устойчивости;

∆ = 0,05;

 – затухание за один период. Обычно лежит в диапазоне 0,90…0,98;

 = 1,5 – колебательность;

Т₀ = Т_РЕГ = 1 с – длительность переходного процесса.

В результате получим